Раздел 1 Постулаты квантовой механики. Операторы.

Микромир для нас непосредственно не наблюдаем. О движении микрочастиц можно судить лишь по тем макроскопическим эффектам, которые они вызывают. Наукой, описывающей поведение микрочастиц, является квантовая механика. Как и любая научная дисциплина, квантовая механика имеет свои постулаты. Следствия, вытекающие из постулатов квантовой механики, многократно подтверждены экспериментально, и это является подтверждением их правильности. Рассмотрим постулаты квантовой механики.

1. Вся информация о физической системе содержится в функции состояния. Функцию состояния называют также волновой функцией и обозначают через . Под физической системой понимают то, что подлежит изучению: электрон, нуклон, фотон и т.п. или любую их комбинацию. В результате изучения физической системы получают набор действительных чисел: значения координат, импульса, энергии и т.п. В квантовой механике предполагается, что информация об этих числах, то есть о поведении физической системы, содержится в волновой функции . О явном виде функции состояния изначально известно только, что она каким-то образом зависит от координат частиц, составляющих систему, и от времени. Для одной частицы

=( x,y,z,t), (1)

где x,y,z – декартовы координаты, t- время. Произведение dx^.dy^.dz=dV называется элементарным объемом. На -функцию накладываются следующие ограничения: она должна быть в своей области определения непрерывной, однозначной и квадратично интегрируемой. Эти требования являются органичными следствиями того, что квадрат волновой функции есть плотность вероятности нахождения частицы в бесконечно малой окрестности некоторой точки с координатами (x,y,z), а вероятность не может иметь разрывов, не может иметь несколько значений при одном и том же наборе аргументов и вычисляется путем интегрирования плотности вероятности по объему всего пространства. Задача состоит в том, чтобы извлечь требуемую информацию из функции состояния . Способ извлечения информации из -функции устанавливается следующими постулатами.

2. Каждой физической величине (энергии, импульсу и т.д.) ставится в соответствие определенный оператор. - ОПЕРАТОР - Под оператором 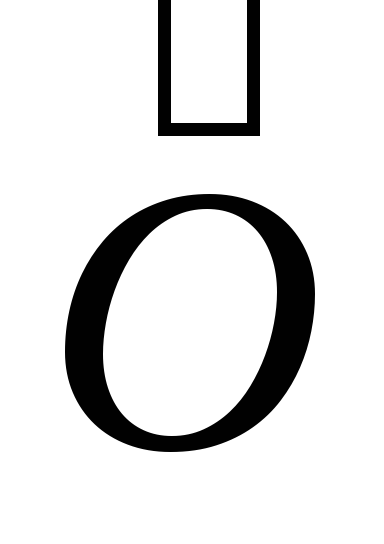понимают действие, производимое над некоторой функцией. Этим действием может быть любое математическое действие – умножение на число, извлечение корня, дифференцирование, интегрирование и т.д.

• ЛИНЕЙНЫЙ ОПЕРАТОР - В квантовой механике используются только линейные операторы, то есть такие, которые подчиняются правилу

(2)

где С₁ и С₂ – произвольные постоянные, а f₁ и f₂ – произвольные функции. Простейшим примером такого оператора может служить наиболее часто используемый в квантовой механике оператор дифференцирования. Действительно, производная от суммы функций есть сумма производных этих функций. А вот, например, оператор извлечения корня не является линейным.

В квантовой механике каждой физической величине ставится в соответствие линейный оператор. Основными являются следующие операторы:

• оператор координаты, который есть умножение на саму координату:

(4)

- оператор импульса.

Импульс – вектор. Обозначим проекции импульса на оси координат через p_x, p_y, p_z. Этим составляющим соответствуют следующие

• операторы проекции импульса

(5)

где , = 1,05^.10^-34 Дж^.с – постоянная Планка.

Оператор полного импульса является вектором, как и сам импульс. Если обозначить единичные вектора вдоль декартовых осей через e_x,e_y,e_z, тогда вектор импульса равен р=e_xp_x+e_yp_y+e_zp_z Тогда

• оператор полного импульса

(6)

- оператор энергии

Ввиду исключительной важности линейных операторов для квантовой механики остановимся на их свойствах подробнее. Пусть имеется линейный оператор . Подберем такую функцию_n , чтобы результат действия на нее оператора сводился к умножению функции_n на постоянный множитель  _n, чтобы выполнялось соотношение . В этом случае _n – собственная функция оператора , а число _n – собственное значение, соответствующее этой собственной функции. Обычно у оператора существует несколько (а в квантовой механике – бесконечно много) собственных функций и собственных значений. В общем случае собственные значения могут быть любыми – и комплексными, и вещественными. В квантовой механике рассматриваются лишь такие операторы, собственные числа которых вещественны. Это и понятно, поскольку физическое содержание собственных чисел – это те самые значения физической величины (соответствующей данному оператору), которые можно измерить экспериментально. Например, если в результате действия оператора импульса на волновую функцию состояния, скажем, электрона, получим собственное число р, то это число и есть значение импульса этого электрона в этом состоянии. Достоинство квантовой механики состоит в том, что абстрактные, казалось бы, действия операторов с абстрактной волновой функцией позволяют получить набор чисел, которые могут быть измерены и проверены экспериментально.

Далее, любая физическая величина, которая может быть измерена экспериментально, является вещественной. В связи с этим – следующий постулат:

3. Единственно возможными значениями физической величины являются собственные значения ее оператора. В классической механике физические величины могут принимать любые значения. Например, энергия колеблющейся частицы E=mv²/2+kx²/2 может быть любой в зависимости от величины скорости v и координаты x. В квантовой механике дело обстоит иначе. Третий постулат утверждает, что для определения возможных значений физической величины надо найти собственные значения  _n уравнения 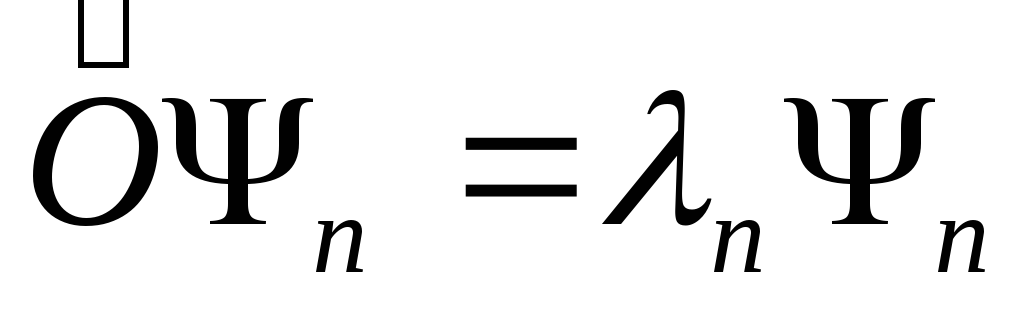, где 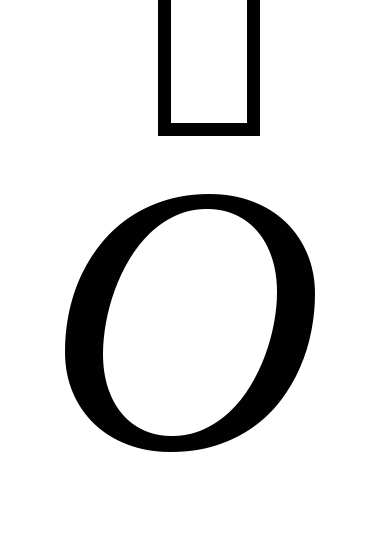- оператор, соответствующий интересующей нас физической величине, а- функция состояния. Этот постулат дает способ построения уравнений квантовой механики и решения наиболее важной задачи – определения возможных значений физической величины. Чтобы определить, какие значения может принимать данная физическая величина, необходимо составить для нее уравнение классической механики (уравнение сохранения), заменить величины, входящие в уравнение классической механики соответствующими операторами и найти собственные значения полученного оператора.

4. Поскольку волновая функция является функцией принципиально комплексной, то согласно правилам ТФКП (теории функции комплексной переменной) квадрат ее модуля определяется, как

, (7)

где через ψ* обозначают функцию комплексно сопряженную к ψ. А постулат звучит так:

Квадрат модуля функции состояния есть плотность вероятности того, что частица находится внутри малого объема dV=dx^.dy^.dz^. в окрестности точки (x,y,z). Например, в одномерном случае (когда ) вероятность нахождения частицы в интервале (х₁,х₂) вычисляется, как

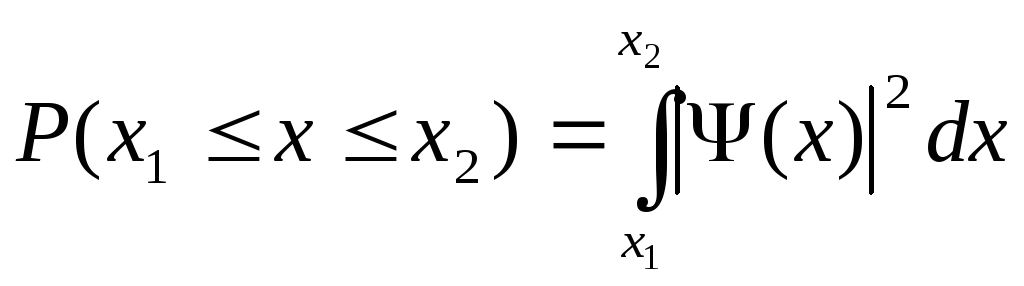(8)

Если точно известно, что некая частица в пространстве существует, то вероятность того, что она находится внутри этого пространства, равна единице, тогда

(9)

Последнее равенство является условием нормировки волновой функции. Следует подчеркнуть, что сама волновая функция физического смысла не имеет, это «всего лишь» функция, правда, содержащая в себе всю возможную физическую информацию о частице.

Таким образом, в соответствии с изложенными выше положениями квантовой механики, состояние микрочастицы или системы микрочастиц носит вероятностный характер и описывается вероятностными законами. В классической статистической физике при описании системы, состоящей из многих частиц, также используются вероятностные законы. Имеется, однако, принципиальное различие между вероятностными предсказаниями классической статистической физики и квантовой механики. В статфизике вероятностные распределения являются результатом взаимодействия большого числа частиц, поведение же каждой отдельной частицы подчиняется законам классической механики. В квантовой механике поведение даже одной частицы описывается вероятностными законами.