26. Формула Тейлора.

Пусть функция f(x) имеет непрерывные производные вплоть до (n+1)-го порядка включительно в некоторой окрестности точки х=а, тогда имеет место формула Тейлора:

. R_n(x) - остаточный член, который может быть представлен в виде: (2) - форма Лагранжа, где -расположена между точками х и а. Другой вид:

27. Ряды Тейлора и Маклорена.

; f(x)=S_n(x)+R_n(x) (6); f(x)-S_n(x)=R_n(x) (6). Потребуем, чтобы функция f(x) имела бесконечное число производных f⁽ⁿ⁾(x) в точке x=а и её окрестности. Получим:

lim (f(x)-S_n(x))=lim R_n(x)=0 (7) . Если lim R_n(x) сущ-ет и равен 0, то f(x)=lim S_n(x) (8)  (9) - ряд Тейлора. При а=0 получаем ряд Маклорена:

.

Замечание Функция представлена в форме ряда Тейлора в том случае если R_n(x)0.

28. Теорема о представлении степенных рядов рядом Тейлора.

Если функция f(x) представима степенным рядом f(x)=a_n(x-a)ⁿ,

то этот степенной ряд явл-ся рядом Тейлора : f(x)= (x-a)ⁿ, т.е. a_n= (11). И такое разложение единственно и коэффициенты нах-ся по формуле (11).

29. Теорема (достаточный признак сход-ти степенного ряда к функции f или представлении в виде ряда Тейлора).

Пусть f⁽ⁿ⁾(x)C=const n=0,1,2... в некоторой замкнутой окрестности точки аХ, тогда функция f представима степенным рядом Тейлора.

31. Ряды Фурье.

Далее мы будем рассматривать глобальное разложение, то есть на конечном отрезке [a,b].

Определение. Понятие ортогонольных и нормированных систем ф-ий:

(х), (х) интегрируемые при х[a,b], тогда (*) - cкалярное произведение.

для (*) вып-ся аксиомы скалярного произведения:

А1 (,)=(,)

А2 (,)=(,)=(,), =const

А3 (,₁+₂)=(,₁)+(,₂)

Определение: Функции  и  на [a,b] ортогональны если (,)=0, т.е. (х)(х)dx=0.

Определение. Понятие нормированности: =- норма (длина вектора).

Докажем, что норма обладает всеми св-вами длины:

=[²(x)dx]^0.5

A.1 0, =0  0

A.2 =, R¹

A.3 ₁+₂=₁+₂

Определения: Если для системы функций ₁,₂,...,_n введено понятие нормы, то такая система наз-ся нормированной. Если норма каждого элемента пространства равна 1, то наз-ся нормированной на 1. Если система функций попарно ортогональна и нормированная на 1, то такая система наз-ся ортонормированной: ОН - ортонормированная система, если

; ОН 

Ряд Фурье. Коэфициенты Фурье по ОН системе.

{₁(x),₂(x),...,_n(x)} - ОН система, т.е. 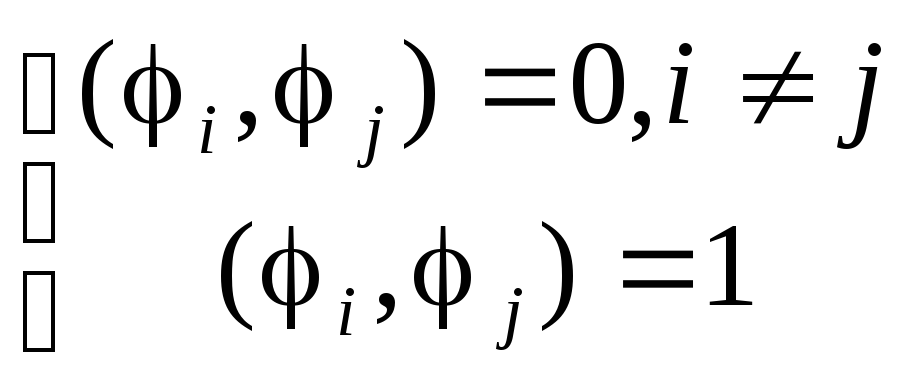. f(x)=f_n_n(x) - ряд Фурье, где f_n - коэфициенты. Умножим обе части этого уравнения на _m(x) и проинтегр:

f(x)_m(x)dx==_m(x) f_n_n(x)dx=f_n_m(x)_n(x)dx=0 - когда mn. Когда m=n:

=f_n(_n,_n)=f_n=f(x)_n(x)dx  f(x)  (f,_n)_n(x)

32. Ряд Фурье для тригонометрических функций.

, f(x) (a_ncos(nx)+b_nsin(nx)) (4)

где a_n=f(x)cos(nx)dx, b_n=f(x)sin(nx)dx, n=0,1,2,...

Определение: Функция называется кусочно-непрерывной на данном отрезке, если этот отрезок можно разбить на конечное число интегралов, в каждом из которых функция непрерывна.

Теорема Дирихле: Пусть f(x)

1)определена для всех х[-,]

2)кусочно-непрерывная на [-,]

3)кусочно-монотонная на [-,]

4)ограничена на [-,], тогда она разложима в тригонометрический ряд Фурье (4). Если точка х[-,] и в этой точки f(x) непрерывна, то сумма ряда

S(x)=(a_ncos(nx)+b_nsin(nx))=f(x). Если точка х - точка разрыва, скачок, то S(x)=^1/2 [f(x-0)+f(x+0)]

S(-)=S()=^1/2 [f(+0)+f(-0)]

Замечания:

1)поведение функции f за пределами [-,] может в корне отлич от значения S.

2)если мы хотим разложить f на всей действительной оси, то согласно (4) мы должны продолжить периодическим образом с периодом 2.