Ортогон_преобразования

12. Ортогональные преобразования.

Опр.1 Линейное преобразование в евклидовом пространстве наз-ся ортогональным, если оно сохраняет скалярное произведение, т.е. ,

. (1)

Предложение 1. Ортогональное преобразование имеет обратное преобразование и

Действительно, из (1)

Следствие. В ортонормированном базисе ортогональное преобразование имеет ортогональную матрицу: определитель матрицы ортогонального преобразования равен

Опр.2 Если , то преобразование называется собственным, если , то несобственным.

Предложение 2. Если - подпространство, инвариантное относительно ортогонального преобразования , то (ортогональное дополнение) – также инвариантное подпространство.

Док-во:

Пусть , т.е. т.к. оно не вырождено взаимооднозначно .■

Задача. Доказать, что произведение двух собственных и двух несобственных ортогональных преобразований есть собственное. Собственное получается непрерывным переходом из единичного, несобственное – после отражения.

Изучим ортогональные преобразования в одно- и двумерных пространствах. Изучение ортогональных преобразований в числе измерений сводится к их изучению.

Если n=1 , то - вектор, задающий одномерное пространство. - ортогональное преобразование. Пусть

в одномерном пространстве есть лишь два ортогональных преобразования: - собственное, и - несобственное.

Рассмотрим ортогональное преобразование в двумерном пространстве , - задается матрицей

А) собственное преобразование, т.е. Из ортогональности Пусть , т.е. всякое собственное ортогональное преобразование в двумерном пространстве имеет матрицу в ортонормированном базисе (поворот на ).

Б) несобственное преобразование, т.е. характеристическое уравнение имеет вид: имеет вещественные корни пусть - собственное значение , т.е. Из ортогональности

Пусть - ортогонален и так как ортогональные преобразования не меняют углов между векторами и их длин в базисе имеет вид

Т.к. возможны два случая:

и (зеркальное отражение относительно одной из осей).

Найдем теперь простейший вид ортогонального преобразования в .

Лемма 1. У всякого линейного преобразования в вещественном пространстве одномерное или двумерное инвариантное подпространство.

Док-во:

Пусть - базис в и - матрица в базис . Рассмотрим характеристическое уравнение .

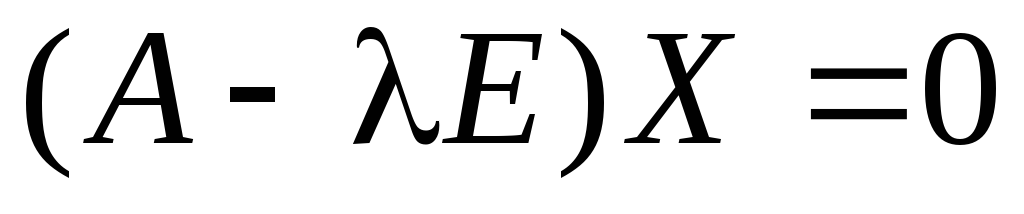
1. Если - корень вещественное решение системы этот порождает одномерное инвариантное подпространство.

2. Пусть - решение системы выделяя вещественную и мнимую часть, получим:

Пусть , Тогда что означает, что - двумерное инвариантное подпространство.■

Теорема. Пусть Â – ортонормированное преобразование в n – мерном евклидовом пространстве . В существует ортонормированный базис , в котором Â имеет вид

(2)

Все элементы, кроме выписанных, равны нулю.

Доказательство. По лемме 1, в можно выбрать либо одномерное, либо двумерное инвариантное подпространство.

Если это одномерное подпространство, то выберем базисный вектор e: . Тогда .

Если двумерное подпространство, то пусть - ортонормированный базис, следовательно, Â – собственное ортогональное преобразование, имеющее матрицу

(3)

(см. лемму 1).

Совокупность векторов, ортогональных выбранным инвариантным подпространствам ( или ) есть снова инвариантное подпространство, следовательно, процедуру можно продолжить.

Таким образом, получено n попарно ортогональных векторов, в базисе этих векторов матрица линейного преобразования имеет вид (2). Одномерные клетки с отвечают одномерным инвариантным подпространствам, а клетки (3) – двумерным. ■