Поверхности второго порядка

§15. Поверхность второго порядка в трёхмерном пространстве.

1°. Основные виды поверхностей второго порядка.

Пусть в трёхмерном пространстве задана, декартова прямоугольная система координат.

Рассмотрим уравнение

,

(1)

где среди коэффициентов хотя бы один отличен от нуля. Множество точек пространства с координатами , удовлетворяющих уравнению (1), определяет, вообще говоря, некоторую поверхность, называемую поверхностью второго порядка. Если уравнение (1) не имеет ни одного решения, то будем говорить, что оно определяет мнимую поверхность.

В некоторых случаях уравнение (1) может определять пару различных или совпадающих плоскостей или одну единственную точку. Но и такие множества будем называть поверхностями.

Перечислим важнейшие частные случай уравнения (1):

1. Эллипсоид

.

2. Однополостный гиперболоид

.

3. Двуполостный гиперболоид

.

4. Эллиптический параболоид

.

5. Гиперболический параболоид

.

6. Конус второго порядка

.

7. Точка

.

8. Цилиндры второго порядка:

цилиндр эллиптический

,

цилиндр гиперболический

,

цилиндр параболический

,

пара пересекающихся плоскостей

,

пара параллельных или совпадающих плоскостей

,

,

прямая

.

Остановимся теперь лишь на более подробном изучении уравнений и описываемых ими поверхностей, указанных выше восьми типов.

Эллипсоид

.

(2)

При эллипсоид (2) обращается в сферу радиуса с центром в начале координат, т.е. геометрическое место точек, отстоящих от начала на расстоянии .

Величины называются полуосями эллипсоида.

Если в уравнении (2) заменить (одновременно или порознь) на , на , на , то оно не изменится, – это показывает, что эллипсоид (2) есть поверхность, симметричная относительно координатных плоскостей и начала координат. Поэтому достаточно изучить уравнение эллипсоида (2) в первом октанте (системы координат), т.е. для . Часть эллипсоида, находящаяся в первом октанте, определяется явным уравнением, например

.

Для определённости будем считать, что . Эллипсоид есть ограниченная поверхность. Он находится внутри шара радиуса с центром в начале координат: для координат любой точки эллипсоида имеет место неравенство

.

Чтобы составить более точное представление об эллипсоиде, произведём сечения плоскостями, параллельными координатным плоскостям. Например, пересекая эллипсоид плоскостями , получим в сечении эллипсы

с полуосями

.

Отсюда видно, что самый большой эллипс получается в сечении эллипсоида плоскостью . Аналогичная картина будет при сечении плоскостями , .

Эллипсоид (2) имеет вид, изображенный на рис. 1.

Рис. 1.

Точки , , лежат на эллипсоиде (2) и называется его вершинами.

Если какие–либо две полуоси равны между собой, то эллипсоид (2) будет эллипсоидом вращения, т.е. получается от вращения эллипса относительно соответствующей оси координат.

Однополостный гиперболоид

.

(3)

По виду уравнения (3) заключаем, что однополостный гиперболоид является поверхностью, симметричной относительно координатных плоскостей и начала координат. Числа называются полуосями однополостного гиперболоида. Точка , , лежащие на поверхности (3), называются вершинами однополостного гиперболоида.

Пересечём поверхность (3) плоскостью , тогда в сечении получим эллипс

с полуосями

.

При изменении от до этот эллипс описывает поверхность (3).

Если теперь пересечь поверхность (3) плоскостью (или ), то получим в сечении гиперболу

.

При первая гипербола распадается на две прямые .

Если , то действительной осью симметрии соответствующей гиперболы является прямая, параллельная оси , а при – прямая, параллельная оси .

Действительной осью симметрии гиперболы мы называем ту из осей симметрии, которую гипербола пересекает.

Если , то поверхность (3) в сечении плоскостями будет иметь окружности радиуса . Поверхность (3) в этом случае образуется от вращения гиперболы около оси . Общий вид однополостного гиперболоида изображён на рис. 2.

Двуполостный гиперболоид

.

(4)

Так как уравнение (4) содержит только квадраты переменных, то данная поверхность симметрична относительно плоскостей , , и начала координат.

Уравнение (4) запишем ещё в виде

.

()

Отсюда ясно, что, пересекая поверхность () плоскостью , получим в сечении эллипс

с полуосями

.

При число , и поэтому нет точек пересечения поверхности () и плоскости .

Рис. 2.

Рис. 3.

При сечении поверхности (4) плоскостями получим гиперболы

.

Точки лежат на поверхности (4) и называются вершинами двуполостного гиперболоида. Поверхность (4) изображена на рис. 3.

Эллиптический параболоид

.

(5)

Так как (5) присутствуют квадраты переменных и , то данная поверхность симметрична относительно координатных плоскостей , . Далее, так как мы считаем , то поверхность (5) расположена в полупространстве .

Пересекая поверхность (5) плоскостями , в сечении будем получать эллипсы

с полуосями

.

При изменении от нуля до данные эллипса описывают нашу поверхность (5).

Пересекая поверхность (5) плоскостями (или ), мы получим в сечении параболы

со смещённой вершиной в точке .

При поверхность (5) будет поверхностью вращения, получающейся от вращения параболы около оси . В этом случае поверхность (5) называют параболоидом вращения.

Точка лежит на поверхности (5) и называется вершиной эллиптического параболоида. Эллиптический параболоид изображён на рис. 4.

Гиперболический параболоид

.

(6)

По виду уравнения (6) заключаем, что данная поверхность симметрична относительно плоскостей , . Пересекая поверхность (6) плоскостями , мы будем получать в сечении гиперболы

,

причём при действительная ось симметрии гиперболы будет параллельной оси , а при – оси . При в сечении будут две пересекающиеся прямые.

При сечении поверхности (6) плоскостями или , получим параболы, направленные ветвями вниз или вверх:

.

Поверхность (6) изображена на рис. 5.

Рис. 4.

Рис. 5.

Конус второго порядка

.

(7)

Данная поверхность симметрична относительно плоскостей , , и начала координат.

При сечении поверхности (7) плоскостями будем получать эллипсы

с полуосями и .

Если же пересекать поверхность (7) плоскостями или , то в сечении получим гиперболы

.

Если теперь пересекать (7) плоскостями , то в сечении получим пару пересекающихся прямых

.

Вид конуса изображён на рис. 6.

Рис. 6.

Точка

.

(8)

Уравнению (8) удовлетворяет только одна точка .

Цилиндры второго порядка

а) Эллиптический цилиндр

.

(9)

Уравнение (9) не содержит переменной . На плоскости уравнение (9) определяет эллипс с полуосями и . Если точка лежит на этом эллипсе, то при любом точка лежит на поверхности (9). Совокупность таких точек есть поверхность, описанная прямой, параллельной оси и пересекающей эллипс

в плоскости .

Эллипс (9) называют направляющей линией данной поверхности, а все возможные положения движущейся прямой – образующими.

Вообще поверхность, описываемая прямой, остающейся параллельной некоторому заданному направлению и пересекающей данную линию , называется цилиндрической. Поверхность (9) изображена на рис. 7.

Рис. 7.

б) Гиперболический и параболический цилиндры

,	(10)
.	(11)

В данном случае направляющими линиями поверхностей являются гипербола и парабола, а образующими – прямые, параллельные оси и проходящие через гиперболу и параболу в плоскости . Поверхности (10) и (11) изображены на рис. 8 и 9.

Рис. 8.

Рис. 9.

в) Параллельные и пересекающиеся плоскости. Прямая

,	(12)
,	(13)
,	(14)
	(15)

Для поверхности (12) направляющими являются прямые линии

.

Поэтому поверхность (12) есть пара пересекающихся плоскостей. В уравнении поверхностей (13) и (14) отсутствуют по две координаты. Уравнение (13) в плоскости есть пара прямых .

Если мы будем брать и любые и , то точки будут удовлетворять уравнению (13), поэтому поверхность (13) есть пара параллельных плоскостей.

Уравнение (14) описывает плоскость , так как этому уравнению удовлетворяют любые точки вида , всё множество которых и составляет плоскость .

Можно также рассматривать как направляющую в какой–либо из плоскостей или , а образующими являются прямые, параллельные оси или оси и проходящие через прямую .

Уравнению (15) удовлетворяет любая точка с и любым . Поэтому (15) изображает прямую, а именно, ось .

Линейчатые поверхности

Некоторые второго порядка образованы движением прямой. Такими являются все цилиндрические поверхности и конус второго порядка. Однако имеются и другие поверхности, которые также образуются движением прямой.

Поверхность, образованная движением прямой, называется линейчатой, а целиком лежащие на ней прямые – прямолинейными образующими.

К линейчатым поверхностям относятся однополостный гиперболоид и гиперболический параболоид.

Уравнение однополостного гиперболоида (3) можно записать в виде

или, разлагая левую и правую части на множители, получаем

.

(16)

Составим систему уравнений первой степени:

(17)

где – произвольный параметр.

При определённом значении этого параметра мы получим прямую линию, а при изменении – семейство прямых. Если мы перемножим уравнения (17) почленно, то получим уравнение (16) нашей поверхности. Поэтому любая точка , удовлетворяющая системе (17), находится на поверхности (16). Следовательно, каждая из прямых семейства (17) целиком лежит на поверхности однополостного гиперболоида.

Совершенно аналогично система

(18)

где – параметр, также определяет семейство прямых, отличное от семейства (17), принадлежащее поверхности (16).

Через каждую точку гиперболоида (16) проходит по одной прямой каждого семейства, вообще при различных значениях параметров и (рис. 10).

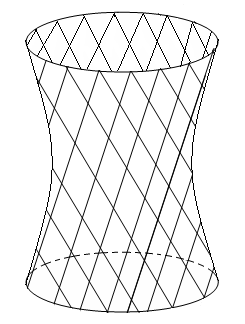
Рис. 10.

2°. Исследование общего уравнения второго порядка с тремя переменными.

Пусть поверхность второго порядка задана уравнением (1):

.

Также как и в случае линий второго порядка, путём преобразований поворота и переноса координатной системы уравнения (1) сложно привести к некоторому каноническому виду. Оказывается, существует ровно 17 типов канонических уравнений второго порядка, которые и будут получены ниже.

Вначале рассмотрим квадратичную форму

,

фигурирующую в левой части уравнения (1). На основании теоремы 1 из §13 существует ортогональное преобразование базисных векторов (представляющее собой преобразование поворота) такое, что в левом базисе квадратичная форма имеет диагональный вид: