рацион_дроби S

§ 4. Поле рациональных дробей

1^о. Эвристические соображения.

В анализе изучаются дробно-рациональные функции вида , где − многочлены. Мы их будем рассматривать как формальные выражения. При этом используем обычные операции :

, где ; ;

.

В этом случае две дроби определяют одну и ту же рациональную функцию.

2^о. Точные определения.

Пусть – поле, – кольцо многочленов над .

Определение 1. Если задача пары многочленов , где , то символ называется рациональной дробью с числителем и знаменателем .

Замечание. Здесь используется термин «символ», т.к. мы не делим многочлены, хотя и иногда их можно разделить без остатка.

Определение 2. Рациональные дроби и называются равными, если в кольце имеется равенство

.

(1)

Свойства рациональных дробей.

1. дробь равна самой себе.

2. Свойство транзитивности: если и .

Действительно, , . Далее после деления на получим доказываемое равенство, т.к. – кольцо без делителей нуля.

Объединим все равные между собой дроби в один класс. Тогда множество всех рациональных дробей разбивается на непересекающиеся классы равных между собой дробей. На множестве этих классов мы хотим определить операции так, чтобы оно было полем. Для этого надо проверять, что замена представителя класса другим не изменяет результат с точки зрения принадлежности классу.

Лемма 1. Рациональная дробь превращается в равную дробь, если её знаменатель и числитель умножаются или сокращаются на один и тот же многочлен, отличенный от нуля.

Доказательство. Действительно, так как из и можно разделить на , то получаем, что операция не выводит из класса равных дробей. ■

Сложение рациональных дробей определим как

\

(2)

Покажем, что если складывать дробь одного класса с дробью другого класса, то результаты всегда лежат в одном и том же третьем классе. Этот класс называется суммой классов. Действительно, пусть

, | умножая первое на , а второе на и складывая | , ч.т.д.

Коммутативность сложения классов из (2), а ассоциативность доказывается прямыми вычислениями.

Дроби вида равны между собой и образуют нулевой класс. Это класс является нулем относительно сложения. Действительно, . Из равенства противоположного класса.

Умножение определим формулой

(3)

Покажем, что произведение дроби одного класса на дробь другого класса дает дроби из одного и того же третьего класса.

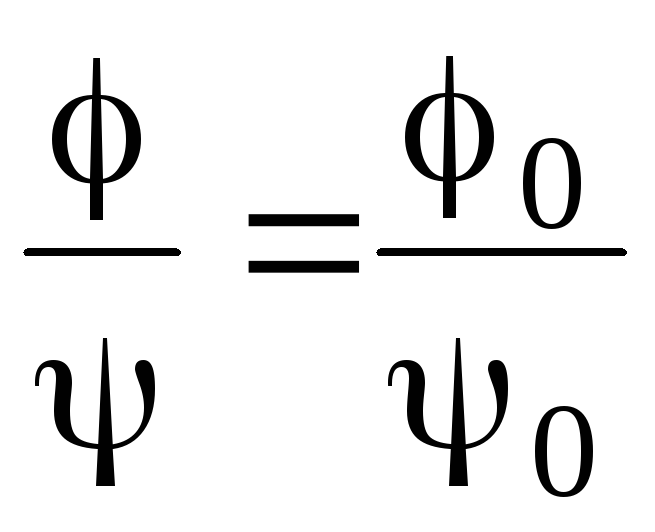
Пусть , можно говорить о произведении классов равных между собой дробей.

Коммутативность и ассоциативность из (3), а дистрибутивность доказывается прямыми вычислениями.

Элементы вида образуют класс, являющийся единицей.

Если не принадлежащий нулевому классу, т.е. определён класс − обратный класс к . Т.о., классы равных между собой рациональных дробей с коэффициентами из образуют поле, обозначаемое , – поле рациональных дробей.

Многочлены образуют подмножество в множестве рациональных дробей такое, что оно образует кольцо.

Замечание. Аналогично для кольца Z из поля .

Определение 3. Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя.

Замечание. Дроби вида являются правильными.

Лемма 2. Всякая рациональная дробь представима, притом единственным способом, в виде суммы многочлена и правильной дроби.

Доказательство. Пусть дана рациональная дробь . Разделим на :

, где . Если наряду с полученным равенством имеет место . Слева – многочлен, справа – правильная дробь , что и требовалось доказать. ■

Напоминание. Над неприводимые многочлены имеют вид : , и , т.е. Над неприводимы многочлены .

Определение 4. Правильная рациональная дробь называется простейшей, если её знаменатель является степенью неприводимого многочлена , т.е. , и .

Теорема 1. Всякая правильная дробь разлагается в сумму простейших.

Доказательство. Вначале рассмотрим правильную рациональную дробь , где − взаимно простые, т.е. . Тогда найдутся многочлены такие, что . Отсюда .

Разделим на с остатком: пусть − остаток, т.е. справедливо представление

(4)

где − многочлен. Так как и Из (4) следует, что , где справа стоит сумма правильных дробей.

Если хотя бы один из знаменателей разлагается в произведение взаимно простых множителей, то можно выполнить дальнейшее разложение. Продолжая далее, получаем, что всякая правильная дробь разлагается в сумму нескольких правильных дробей, каждая из которых имеет знаменателем степень некоторого неприводимого многочлена. А именно, если для имеем, что , где , если , то

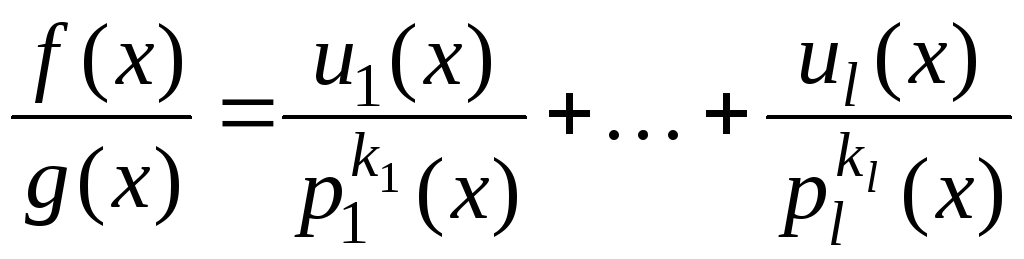, где справа стоят правильные дроби.

Осталось рассмотреть , где это правильная дробь, p(x) – неприводимый многочлен. Применим алгоритм деления с остатком и разделим на , остаток разделим на , и т.д. Имеем :

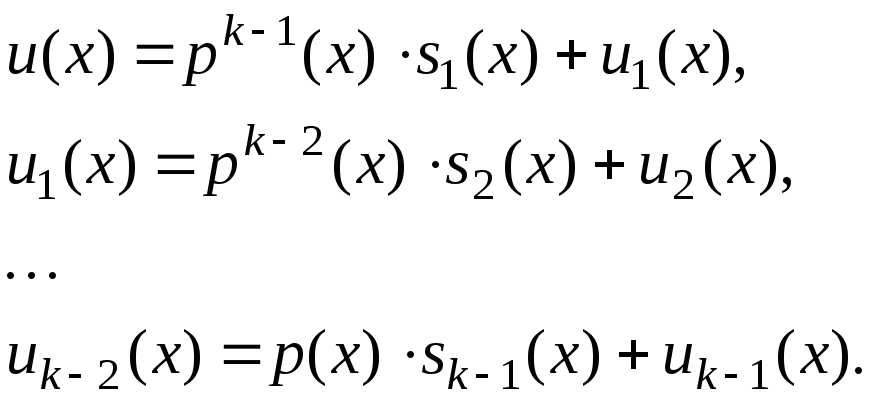
Так как степень меньше чем степень , а степень каждого из остатков меньше степени , то степень всех частных меньше, чем степень . Степень последнего остатка меньше, чем степень ,откуда следует, что ,

т.е. получаем:

,

Итак, получено искомое представление. ■

Следствие. Всякая правильная рациональная дробь обладает единственным разложением в сумму простейших дробей.

Доказательство. Пусть это неверно. Тогда вычитая из одного разложения другое, получаем после приведения подобных сумму простейших дробей, тождественно равную нулю. Пусть знаменатели простейших дробей содержат неприводимые многочлены , причём максимальная степень каждого соответственно. Умножим всю сумму на . Тогда все слагаемые, кроме одного – многочлены и осталось слагаемое 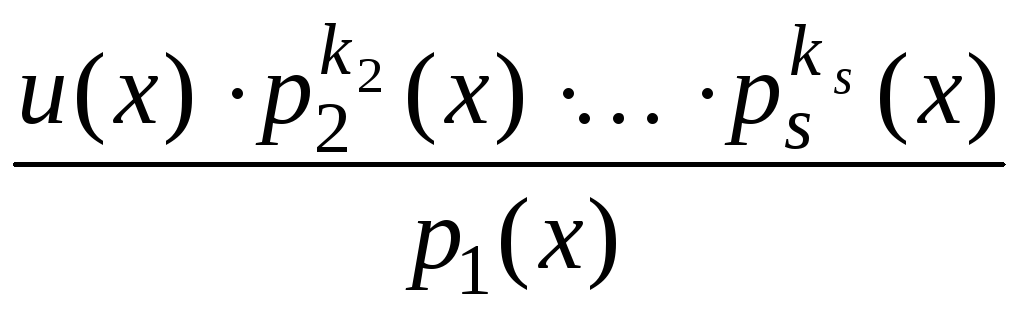. Так как многочлены − неприводимы, то числитель не делится на знаменатель, а все множители с ним взаимно просты противоречие, т.к. нуль представлен в виде суммы многочлена и правильной дроби. ■

Пример. Представим в виде суммы простейших дробей, где

.

Здесь и значит разложение дроби на суму простейших имеет вид .

После приведения к общему знаменателю суммы, стоящей в правой части равенства и приравнивания числителей, получаем:

.

При различных значениях отсюда получаются уравнения на неизвстные коэффициенты :

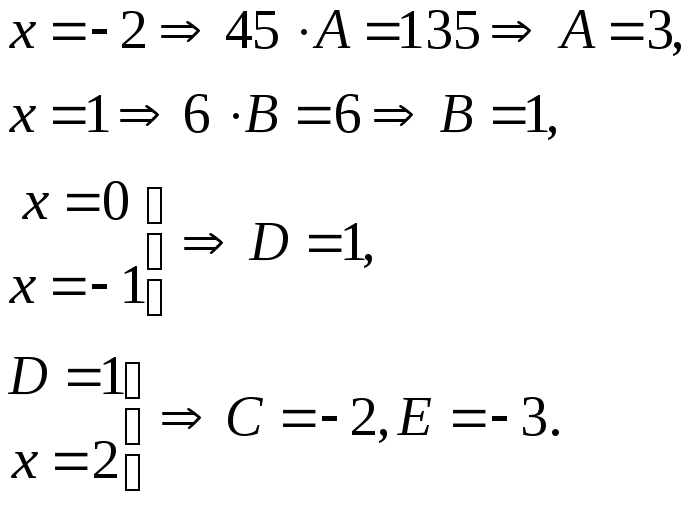
Таким образом, искомое разложение имеет вид:

.

37