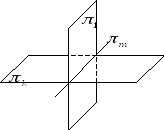
Примеры.

1. , − общее уравнение прямой на плоскости.

2. , − общее уравнение плоскости в пространстве.

3. 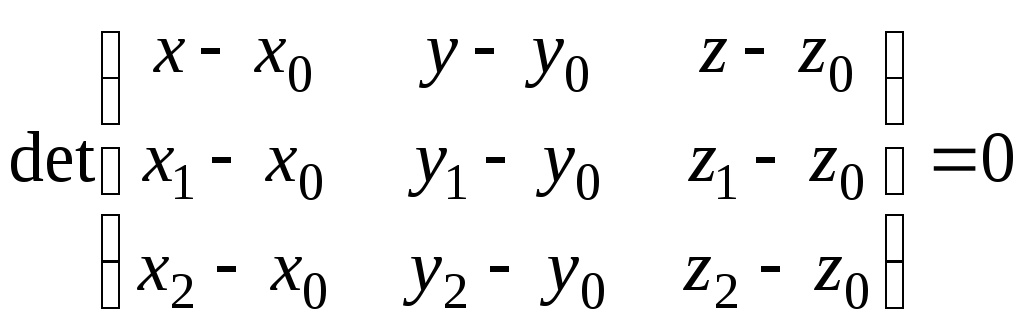− уравнение плоскости, проходящей через три точки.

5˚. Взаимное расположение плоскостей в аффинном пространстве.

Пусть и − две плоскости в аффинном пространстве А, проходящие в направлении и .

А) Пересекающиеся плоскости.

Пусть эти плоскости имеют хотя бы одну общую точку . Если эту точку принять за начало координат, то когда текущая точка пробегает плоскость или , вектор пробегает подпространство или , соответственно. Поэтому пересечение и зависит от того, как пересекаются подпространства и . Из свойств пересечения подпространств следует:

Утверждение 1. Если плоскости и пересекаются, то их пересечением будет некоторая плоскость . Соответствующее направляющее пространство .

В частности, может быть так, что , т.е. пересечение происходит по одной точке. Это возможно, лишь при условии, что .

Случай , (или ), относится к случаю параллельных плоскостей.

Утверждение 2. Если плоскости и пересекаются по , то плоскость : , содержащая и одновременно, причем ни в какой плоскости меньшей размерности и не могут содержаться одновременно. Направляющее подпространство этой плоскости получается как сумма и . Имеем, что

.

(7)

Отметим, что если сумма и прямая, то и имеют единственную общую точку.

Утверждение 3. Если плоскости и содержатся в какой либо плоскости , то размерность их пересечения :

.

(8)

Это утверждение следует из (7).

Б) Параллельные плоскости.

Пусть плоскость проходит через и имеет направляющее подпространство , а плоскость проходит через и имеет направляющее пространство . Будем считать, что .

Определение 2. Будем говорить, что параллельна , если . В этом случае, также будем говорить, что параллельно .

Случай, когда содержится в − частный случай параллельности. Тоже самое справедливо для совпадения плоскостей.

Утверждение 4. Если плоскости и пересекаются в точке и , то содержится в . Если , то и совпадают.

Теорема 3. Гиперплоскость, задаваемая уравнением

,

(9)

совпадает с гиперплоскостью, задаваемой

,

(10)

тогда и только тогда, когда

.

(11)

Гиперплоскости, представляемые уравнениями (9) и (10) параллельны тогда и только тогда, когда

.

(12)

Доказательство: Чтобы гиперплоскости (9), (10) совпадали, необходимо и достаточно, чтобы системы уравнений (9), (10) определяли гиперплоскость. Это, в соответствии с теоремой 2, равносильно тому, что

,

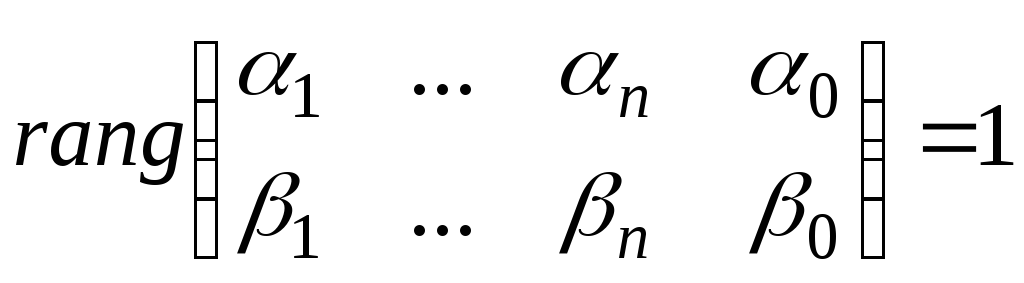что равносильно (11). Гиперплоскости (9), (10) параллельны, если они либо совпадают (тогда имеем (11)), либо не пересекаются. В последнем случае система уравнений (9), (10) должна быть несовместной и поэтому, в силу теоремы Кронекера – Капелли, , т.е. имеет место (12). ■

Пример. Дано уравнение гиперплоскости (9) и координаты некоторой точки . Найти уравнение гиперплоскости, параллельной (9) и проходящей через точку .

Пусть (10) – уравнение искомой гиперплоскости. Так как (9) и (10) параллельны, то справедливо (12) умножая (10) на подходящий множитель, имеем . Так как лежит на этой гиперплоскости, то вычитая это равенство из предыдущего уравнения, получаем искомое уравнение .

Очевидно, что (9) проходит через начало координат . Если , то (9) можно записать в виде − уравнение гиперплоскости в отрезках.

Теорема 4. Для того, чтобы прямая

(13)

была параллельна прямой

(14)

необходимо и достаточно, чтобы их направляющие коэффициенты были пропорциональны:

.

(15)

Прямые (13), (14) совпадают когда выполнены условия пропорциональности (15) и условия , выражающие, что точка с координатами , лежащая на прямой (13), лежит на прямой (14).

Доказательство: Из (13) видно, что на этой прямой лежат точки и направляющее подпространство определяется вектором . Аналогично, для второй прямой направляющее подпространство определяется вектором . Эти прямые параллельны, если вектора и коллинеарны выполняется условие (15). Так как для совпадения прямых достаточно, чтобы они были параллельны и имели хотя бы одну общую точку, то второе условие утверждение теоремы очевидно. ■

Теорема 5. Гиперплоскость, заданная уравнением (9)

(9)

параллельна прямой (13)

(13)

тогда и только тогда, когда

.

(16)

Доказательство: Уравнение (13) перепишем в параметрическом виде: и подставим в (9). Имеем:

(17)

Если , то отсюда находим единственное значение имеем единственную точку, в которой пересекаются прямая и гиперплоскость они не параллельны.

Если в (17) , а правая часть (17) не равна нулю, то уравнение (17) не имеет решений прямая и гиперплоскость не пересекаются они параллельны. Если же правая часть (17) равна нулю, то уравнение (17) справедливо для все точки прямой лежат на гиперплоскости они параллельны. ■

Пусть в произвольной аффинной системе координат заданы две плоскости и одинаковой размерности своими системами ЛНУ. Из определения параллельных плоскостей

Теорема 6. Плоскости и параллельны соответствующие СЛОУ эквивалентны.

Доказательство: Очевидно из теории СЛУ. ■

Теорема 7. Пусть в аффинном пространстве заданы плоскость и точка . Тогда плоскость размерности , проходящая через точку параллельно . Если , то совпадает с , если , то и не пересекаются.

Доказательство: Следует из теоремы 6. ■

В) Скрещивающиеся плоскости.

Определение 3. Две плоскости называются скрещивающимися, если они не пересекаются и не параллельны.

Примером могут служить скрещивающиеся прямые в . С увеличением размерности увеличивается возможность скрещивания.

Пусть в аффинном пространстве имеются две пересекающиеся плоскости и : и , и при этом ни одна из них не лежит в другой. Пусть их пересечением является плоскость размерности : и . Известно, что существует плоскость наименьшей размерности : , содержащая плоскости и .

Теорема 8. Если , то всякая - мерная плоскость, параллельная плоскости , но не содержащаяся в , скрещивается с .

Доказательство: Так как , то существует точка , не принадлежащая . Через эту точку проведем плоскость . Эта плоскость не содержится в , так как в противном случае точка содержалась бы в . Докажем, что плоскости и – скрещивающиеся. Легко видеть, что не параллельна , так как в противном случае либо , либо , что противоречит условию пересечения и . Теперь покажем, что и не пересекаются. Проведем через точку плоскость . Тогда . Если предположить, что пересекает , то тогда будет пересекаться с , что невозможно. Значит, скрещивается с . ■

Следствие. Если целые числа удовлетворяют неравенствам , , , то в найдутся скрещивающиеся плоскости и с направляющими подпространствами и , пересечение которых имеет размерность .

Теорема 9. Существует единственная плоскость размерности , содержащая две скрещивающиеся плоскости и .

Доказательство: Выберем произвольные точки и и рассмотрим вектор . Пусть плоскость содержит плоскости и , и направляющим подпространством для является . Очевидно, что , и также содержатся в содержит их сумму: . Обратно, если – любое подпространство, включающее , то плоскость , проходящая через точку в направлении , будет содержать и . Действительно, так как и . Так как и , то . Значит, так как , то .

Теперь покажем, что плоскость наименьшей размерности имеет в качестве направляющего подпространства –мерное подпространство , построенное выше. Пусть и по введенным обозначениям . Покажем, что . Для этого достаточно показать, что . Пусть : , где и . Так как , то по второй аксиоме аффинного пространства точка : . Тогда по третьей аксиоме , откуда следует, что . Таким образом, , что противоречит условию их скрещивания . ■

Теорема 10. Если скрещивающиеся плоскости и лежат в плоскости , то

.

(18)

Следствие. Если в есть скрещивающиеся плоскости и положительных размерностей, то , .

Эти неравенства следуют из (18) при , так как для скрещивающихся плоскостей , .

Частный случай. Гиперплоскость не может скрещиваться с какой-либо плоскостью положительной размерности.

Теорема 11. (достаточное условие пересечения двух плоскостей). Если в даны плоскости и :

,

(19)

где - размерность пересечения направляющих подпространств и , то и пересекаются.

Доказательство. Исключая тривиальный случай, когда одна из плоскостей есть все , рассмотрим

.

(20)

Возможны три случая: а) , б) и – скрещивающиеся, в) и – пересекаются. Если , то для пересечения имеем, что , что вместе с (20) противоречит (19). Если и скрещивающиеся, то справедливо (18) при , что противоречит также (19). Следовательно, и – пересекаются. ■

Пример. Определить все случаи взаимного расположения двух плоскостей , в –мерном пространстве и найти необходимое достаточное условие каждого из случаев.

Здесь направляющее подпространство плоскости натянуто на , а подпространство плоскости натянуто на . Значит, . Пусть , , , , , .

Взаимное расположение плоскостей и определяется структурой общего решения СЛНУ

(21)

на неизвестные . Структура общего решения системы (21) определяется матрицам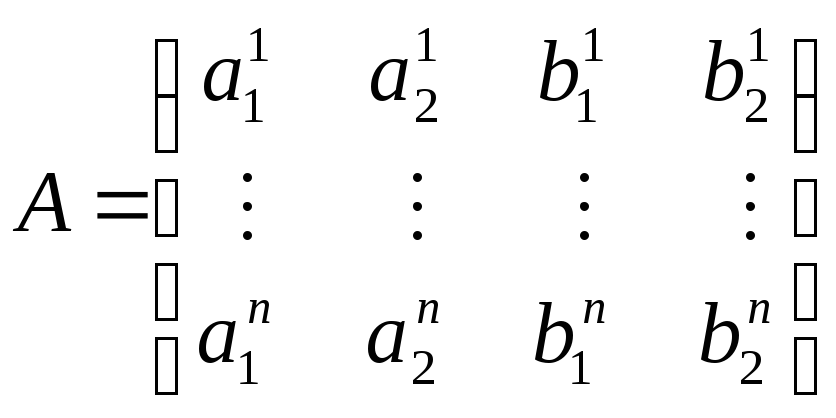и

и .

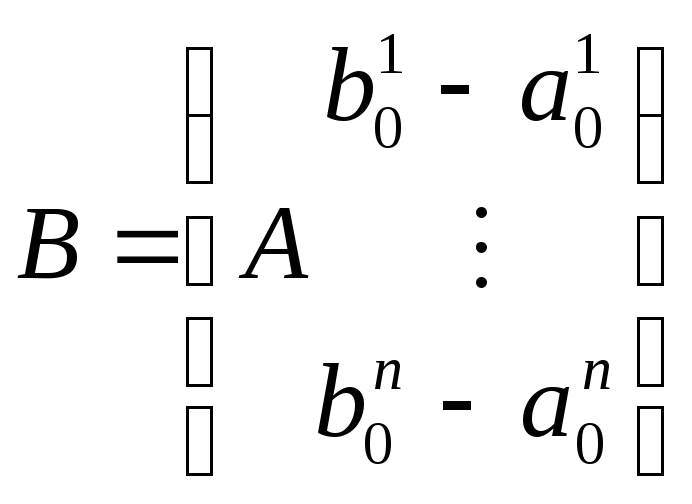1. Если , , то система (21) несовместима плоскости и скрещиваются в пятимерной плоскости. При этом направляющие подпространства и пересекаются по нулевому вектору.

2. Если , , то система (21) имеет единственное решение и содержатся в четырехмерной плоскости и пересекаются в точке.

3. Если , плоскости и принадлежат одному четырехмерному подпространству и скрещиваются. Направляющие подпространства пересекаются по одномерному подпространству.

4. Если , плоскости и содержатся в трехмерной плоскости и пересекаются по прямой.

5. Если , плоскости и лежат в трехмерной плоскости и параллельны.

6. Если , плоскости и совпадают.

25