2.7. Граничні умови електростатики

На рис. 2.9 наведено приклад подання довільного вектора двома складниками: нормальнимвздовж осіу, та тангенціальнимвздовж осіх.

Рисунок 2.9. Вектор та його проекції ,

Аналогічно, на межі двох середовищ з різними значеннями діелектричної проникності (₁та₂) векторита, які описують електричне поле можна подати двома складниками:

– нормальним(проекцією на нормаль до границі – вздовж осіy)

– тангенціальним(дотичним) складником (проекція на границю – вздовж осіх).

2.7.1. Нормальні складники векторів та

Щоб визначити нормальний складникзручнимє вибірвектора як такого, що характеризуєпотік, який пронизує межу двох середовищ.

Рисунок 2.10. До визначення нормальних складників електричного поля

Нехай силові лінії вектора перетинають межу двох середовищ з параметрамита. Цю межу характеризує поверхнева густина заряду:

. (2.59)

Відповідно до закону Гаусса в інтегральній формі маємо визначення потоку вектора , який дорівнює сумарному заряду в об’ємі, обмеженому поверхнеюS:

.

Розглянемо циліндр з поперечним перерізом , верхньою та нижньою основами. Відносно циліндра потік вектора– це сума потоків крізь верхню, нижню та бічну поверхні (рис. 2.10):

. (2.60)

У зв’язку з тим, що заряд зосереджено на поверхні , висоту циліндра можна змінювати без спотворення загального результату. За умови зменшення висоти до нуля з урахуванням (2.59) маємо:

. (2.61)

Перший доданок характеризує стан поля у першому середовищі, а другий – у другому. Зменшуємо площутак, щоб можна було вважати, що в кожній точці цієї поверхні.

Тоді:

, (2.62)

або

. (2.63)

У (2.63) перший доданок – нормальний складник у першому середовищі, а другий – у другому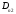. Зауважимо, щотапротилежні за напрямками дота однакові за модулем==.

Тоді, граничні умови для нормального складника вектора :

, (2.64)

тобто нормальний складник вектора за наявності поверхневого заряду змінюється стрибком.

Стосовно складників вектора , маємо:

, (2.65)

В окремому випадку, якщо поверхневий заряд відсутній , то

(2.66)

та

. (2.67)

Отже, нормальний складник вектора напруженості електричного поля також змінюється стрибком.

2.7.2. Тангенціальні складники векторів та

Для визначення тангенціального складника зручнимє вибірвектора , як такого, що характеризуєциркуляціювздовж межі двох середовищ.

Нехай силові лінії перетинають межу двох середовищ з параметрамита. Визначимо циркуляцію. Як відомо, від форми контуру значення циркуляції не залежить, виберемо для зручності контур прямокутної форми, сторони якого нескінченно малі, а напрямок обходу за годинниковою стрілкою (рис. 2.11). Циркуляціяхарактеризує роботу сил поля. За визначенням, дляелектростатики

,

тобто:

. (2.68)

Рисунок 2.11. До визначення тангенціальних складників електричного поля

Якщо наближати контур до межі двох середовищ, то інтеграли тадорівнюють нулю. Тоді із (2.68) маємо

. (2.68а)

Перший доданок характеризує перше середовищі, другий – друге. Сторониabтаcd –нескінченно малі величини й дорівнюють, тому можна вважати, що значенняоднакові, тоді:

(2.69)

З (2.68а) та з урахуванням (2.69) та напрямків обходу контуру, отримаємо:

. (2.70)

З урахуванням, що ab=cdта після скорочення, маємо:

. (2.70а)

Доданки (2.70а) – це тангенціальні складники, які не зазнають розриву

. (2.71)

Стосовно складників вектора маємо:

. (2.71а)