2.5. Градієнт потенціалу. Еквіпотенціальні поверхні

Оскільки електростатичне поле характеризують скалярною неперервною функцією-потенціалом, то в ньому завжди можна виділити геометричне місце точок з однаковим потенціалом. У тривимірному просторі таку поверхню називаютьеквіпотенціальною. Таким чином електростатичне поле можна уявити безліччю еквіпотенціальних поверхонь. Щоб визначити взаємне розташування однієї поверхні відносно іншої, а також відносно силових ліній, тобто структуру поля, пояснимо поняття «градієнт потенціалу» – характеристику, яка визначає зв’язокта.

Градієнт потенціалу– це вектор, який характеризуєінтенсивність змінення скалярної величини , та спрямований у бік її зростання(за нормаллю до відповідної поверхні). Оскільки найінтенсивніша зміна відбувається у напрямку найменшої відстані між поверхнямиS1таS2, то вектор градієнта є перпендикулярним до дотичної стосовно еквіпотенціальній поверхні у конкретній точці та спрямований до більшого значення. Тобто, можна записати:

, (2.42)

де – одиничний вектор вздовж нормалі до поверхні.

Для визначення градієнту в ортогональній системі координат з’ясуємо спочатку похідну потенціалу вздовж довільного напрямкуl(рис. 2.8).

Рисунок 2.8. До визначення градієнта потенціалу

З рис. 2.8 визначимо

. (2.43)

Візьмемо відношення приросту потенціалу до приросту:

, (2.44)

або для нескінченно малих величин:

. (2.45)

Формула (2.45) визначає проекцію вектора на довільний напрямок:

. (2.46)

Якщо довільний напрямок надати у прямокутній системі координат, то отримаємо:

, (2.47)

або:

. (2.48)

Модуль: . (2.49)

Для визначення зв’язку між напруженістю поля з потенціалом нагадаємо співвідношення (2.47), в якому за умови нескінченного зменшення відрізкаabв границіотримано (2.48).

З (2.41) можна записати

. (2.50)

И з урахуванням (2.51) та (2.52) маємо

. (2.51)

Зазначимо, що знак «–» має фізичний зміст, бо напрямки векторівтаgrad–протилежні (рис. 2.8).

Це важливе співвідношення свідчить, що напруженість електричного поля – вектор _, можна визначити як градієнт скалярної величини – потенціалу .

З формули (2.51) випливає, що за значенням потенціалу можна розв’язати пряму задачу електростатики, якщо є зв’язок міжпотенціаломтагустиною заряду- із розв’язкурівняння Пуассона.

2.6. Рівняння Пуассона та Лапласа

Для розв’язання прямої задачі електростатики необхідно визначити три проекції вектора :. Це можливо на підставі(2.46а) та (2.48)

. (2.52)

Нагадаємо закон Гаусса в диференціальній формі (2.33):

.

Підстановкою (2.52) в (2.33), з урахуванням першого матеріального рівняння 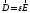, отримаємо:

. (2.53)

З використанням оператора Гамільтона узагальнено запишемо

. (2.54)

Формула (2.54) – це рівняння Пуассона.

Математичний розв’язок цього рівняння:

, (2.55)

де – поточна відстань між елементомта точкою спостереження.

Після інтегрування отримаємо:

. (2.56)

Таким чином, послідовність розв’язку прямої задачі: за (2.54) визначимо потенціал, як функцію розподілу зарядів відносно координат точки спостереження, а далі за відомим потенціалом напруженість поля, як градієнт із протилежним знаком (2.48).

Якщо в деякому об’ємі заряди відсутні, то рівняння (2.53) та (2.54) набувають вигляду:

, (2.57)

або

. (2.57а)

Формули (2.57), (2.57а) – це рівняння Лапласа. Їх застосовують для розрахунку електричних полів в області простору, де заряди відсутні.

Розв’язок рівняння Лапласа визначають як добуток функцій однієї змінної

. (2.58)

Для розв’язку рівняння Лапласа необхідно визначити, яким чином зміняться вектори та_{на межі двох середовищ, де є електростатичне поле.}