2.3. Закон Гаусса

2.3.1. Закон Гаусса в інтегральній формі

Нехай вектор , який створено зарядом, перетинає нескінченно малу площину– плаский елемент поверхні, зорієнтований у просторі. Тобто ця площина має дві характеристики: значення та напрям, як векторна величина, і має назвувектор-площадка. Вектор – перпендикулярний до поверхні, а його значення чисельно дорівнює.

На рис. 2.3 показано орієнтацію вектора та довільного вектора.

Рисунок 2.3. Приклад орієнтації векторів та

Визначимо диференціал потоку вектора :

. (2.12)

Нехай далі маємо замкнену поверхню будь-якої форми, навколо точкового заряду . Замінимочерез значення заряду та відстані за визначенням (2.5), тоді:

, (2.12а)

або

, (2.13)

де – елементарний тілесний кут, за якого можна побачити площину з точки розташування заряду (рис. 2.4)

. (2.14)

Рисунок 2.4. До визначення поняття тілесний кут

Міра тілесного кута – співвідношення площі елемента сферичної поверхні до квадрату відстані з урахуванням орієнтації.

Потік вектора через цю поверхню можна визначити інтегруванням (2.13) за поверхнею(тобто,в межах)

. (2.15)

Нехай в об’ємі, який обмежує поверхню , є безліч зарядів. Тоді, згідно принципу суперпозиції для лінійних середовищ отримаємо сумарний вектор:

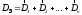. (2.16)

Таким чином, відповідний потік вектора електричного зміщення:

, (2.17)

де .

Тоді

, (2.18)

тобто

. (2.19)

Формула (2.19) визначає закон Гаусса в інтегральній формі та свідчить, що потік вектора електричного зміщення через будь-яку замкнену поверхню дорівнює алгебраїчній сумі зарядів, які розташовано всередині об’єму, обмеженого цією поверхнею. За цією формулою можна розв’язувати пряму задачу електродинаміки – за відомими зарядами визначити характеристики поля та.

Для розв’язання оберненої задачі необхідно мати співвідношення, яке пов’язує вектор із зарядому конкретній точці, тобто визначити диференціальну форму закону Гаусса.

2.3.2. Закон Гаусса в диференціальній формі

Визначимо будь-яку точку (x,y,z) у просторі, в якому є електричне поле. Значення вектора у точціскладено з компонентів:

.

Розглянемо замкнену поверхню, у вигляді елементарного кубу з центром у точці із сторонами довжиною,,(рис. 2.5) та застосуємо закон Гаусса, тобто визначимо потік векторакрізь цей куб за формулою (2.19).

Рисунок 2.5. До визначення закону Гаусса в диференціальній формі. Модель елемента простору в електричному полі

Для визначення цього інтегралу треба розкласти його на шість складників – відповідно кожній грані куба:

. (2.20)

Проаналізуємо детально перший інтеграл для фронтальної поверхні. Оскільки елемент поверхні дуже малий, значення на ньому можна вважати незмінним і тоді:

, (2.21)

де потрібно визначити на цій грані куба,_{, 1234}

Ця грань є на відстані від точки, тому

, (2.22)

де – значення в точці ;

частинна похідна визначає зміненнявздовж осі.

Таким чином із (2.21) з урахуванням (2.22) маємо

. (2.23)

Проаналізуємо інтеграл для протилежної поверхні

. (2.24)

Змінення значення від точкидо площини

. (2.25)

Таким чином із (2.24) із урахуванням (2.25) маємо

. (2.26.)

Додамо інтеграли (2.23) та (2.26), й отримаємо:

. (2.27)

За таким саме принципом отримаємо:

(2.28)

та

. (2.29)

Об’єднанням формул (2.27)…(2.29) (за всіма гранями) маємо:

, (2.30)

або

. (2.30а)

Таким чином, застосовано закон Гаусса для обмеженого простору, навколо елементарного об’єму . У результаті маємо формулу, яка показує, що заряд, зосереджений в об’ємі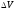, дорівнює

. (2.31)

Тобто за (2.30)…(2.30а) можна визначити, що сума частинних похідних проекцій вектора дорівнює потоку, віднесеному до об’єму за умови прямування об’єму до нуля:

. (2.32)

За визначенням з математики, границя потоку вектора віднесеного до об’єму за умов є дивергенція цього вектора:

. (2.33)

Таким чином можна трактувати дивергенцію, як диференціальну характеристику потоку.

Зауважимо, що операція змінює одиницю вимірювання відповідної функції на(до речі, теж саме притаманне операціямта).

Із застосуванням оператора Гамільтона – «набла» –

, (2.34)

де – одиничні вектори (орти) вздовж координатних осей, відповідно x, y, z;

можна записати:

. (2.35)

Формула (2.35) визначає закон Гаусса в диференціальній формі, тобто, стосовно об’ємної густини заряду, тоді як в інтегральній формі – стосовно заряду (2.19).