
- •4. Основні рівняння електродинаміки. Система рівнянь максвелла
- •4.1. Закон збереження електричного заряду
- •4.2. Перше рівняння Максвелла (закон повного струму)
- •4.3. Друге рівняння Максвелла (закон електромагнітної індукції)
- •4.4. Повна система рівнянь Максвелла
- •4.5. Рівняння Максвелла для монохромного гармонічного коливання (у комплексній формі)
- •4.6. Класифікація середовищ за провідністю
- •4.7. Принцип переставної двоїстості
- •4.8. Явище затримання електродинамічних потенціалів
- •4.9. Висновки
- •4.10. Контрольні питання та завдання
4.8. Явище затримання електродинамічних потенціалів
Функцією, що полегшує розв’язувати задачі електродинаміки, є потенціал. Нагадаємо, що в електростатиці формула для потенціалу (2.60) має вигляд:
 , (4.54)
, (4.54)
а для магнітного поля постійного струму – векторний магнітний потенціал (3.54а):
 , (4.55)
, (4.55)
де
 – відстань
від джерела до точки спостереження в
декартовій системі координат.
– відстань
від джерела до точки спостереження в
декартовій системі координат.
Останні рівняння отримано в результаті розв’язування рівняння Пуассона для електростатики та за аналогією для магнітного поля постійного струму, відповідно:
 , (4.56)
, (4.56)
 , (4.57)
, (4.57)
де
 –
оператор Лапласа (лапласіан).
–
оператор Лапласа (лапласіан).
З іншого боку:
 , (4.58)
, (4.58)
 .
(4.59)
.
(4.59)
Спробуємо визначити
функцію
 ,
якщо струм і заряд є змінними за часом.
Нагадаємо витоки появи вектора
,
якщо струм і заряд є змінними за часом.
Нагадаємо витоки появи вектора
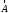 .
З векторного аналізу відомо: якщо
.
З векторного аналізу відомо: якщо
 ,
то існує
деякий вектор,
ротор якого
дорівнює вихідному,
тобто
,
то існує
деякий вектор,
ротор якого
дорівнює вихідному,
тобто
 (див. підрозділ 3.3).
(див. підрозділ 3.3).
Таким чином, якщо
відомі
 (4.54) та
(4.54) та (4.55), можна визначити
(4.55), можна визначити (4.58) та
(4.58) та (4.59), відповідно. Визначимо напруженість
електричного поля для ситуації, якщо
ці процеси змінні в часі (для змінного
джерела). На підставі другого рівняння
Максвелла:
(4.59), відповідно. Визначимо напруженість
електричного поля для ситуації, якщо
ці процеси змінні в часі (для змінного
джерела). На підставі другого рівняння
Максвелла:
 ,
(4.60)
,
(4.60)
з урахуванням (4.59), можемо записати:
 . (4.61)
. (4.61)
Оскільки операція ротор є операцією диференціювання за координатами, то (4.61) можна записати як
 .
(4.62)
.
(4.62)
З векторного
аналізу відомо також, якщо
ротор будь-якого вектора дорівнює нулю,
то існує
скалярна функція, наприклад
 ,градієнт
якої дорівнює цьому вектору,
тобто:
,градієнт
якої дорівнює цьому вектору,
тобто:
 . (4.63)
. (4.63)
Підтвердимо це положення:

 .
.
Якщо
 ,
то (4.63) співпадає із співвідношенням:
,
то (4.63) співпадає із співвідношенням: або (4.58), за умови
або (4.58), за умови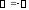 .
Використаємо цю заміну, тому що обмежень
на вибір знаку немає:
.
Використаємо цю заміну, тому що обмежень
на вибір знаку немає: ,
й отримаємо:
,
й отримаємо:
 .
(4.64)
.
(4.64)
Звідси випливає,
що в динамічному процесі на відміну від
статичного режиму, напруженість
електричного поля
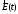 визначає не лише електричний потенціал
визначає не лише електричний потенціал ,
але й змінний за часом векторний магнітний
потенціал
,
але й змінний за часом векторний магнітний
потенціал .
.
Тепер встановимо
зв’язок
 і
і із параметрами першоджерела поля.
із параметрами першоджерела поля.
У першому рівнянні Максвела, в якому (табл. 4.2 – перший рядок – без густини стороннього струму):
 . (4.65)
. (4.65)
Замінимо
 та
та ,
на підставі (4.59) та (4.64):
,
на підставі (4.59) та (4.64):
 . (4.66)
. (4.66)
На підставі
тотожності векторного аналізу


 ,
перестановки доданків та врахуванням
можливості зміни порядку диференціювання
отримаємо:
,
перестановки доданків та врахуванням
можливості зміни порядку диференціювання
отримаємо:
 . (4.67)
. (4.67)
Зауважимо, що в
рівнянні (4.67) є величина, пов’язана зі
швидкістю поширення електромагнітної
хвилі
 :
: .
Це рівняння має нескінченну множину
розв’язків, тому що у ньому дві невідомі
величини
.
Це рівняння має нескінченну множину
розв’язків, тому що у ньому дві невідомі
величини і
і
 .
.
Щоб розв’язати спростимо його; для цього припустимо що:
 . (4.68)
. (4.68)
Це співвідношення називають калібрувальним перетворюванням Лоренца. За такої умови (4.67) спрощується:
 .
(4.69)
.
(4.69)
Звідки випливає,
що векторний потенціал
 визначає
густина струму.
визначає
густина струму.
До речі, якщо
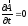 ,
то отримаємо рівняння для магнітного
поля постійного струму (див. (4.57).
,
то отримаємо рівняння для магнітного
поля постійного струму (див. (4.57).
Тепер встановимо
зв’язок потенціалу
 з джерелом через густину заряду
з джерелом через густину заряду .
.
Для цього у третє рівняння Максвелла (див. табл. 4.2):
 , (4.70)
, (4.70)
з урахуванням першого матеріального рівняння (п’яте – Максвелла : табл. 4.2) підставимо значення із (4.64), й отримаємо:
 . (4.71)
. (4.71)
Змінимо порядок диференціювання у (4.71):
 . (4.72)
. (4.72)
З врахуванням, що
з (4.68)
 , а також
що за правилами застосування оператора
Гамільтона
, а також
що за правилами застосування оператора
Гамільтона
 запишемо:
запишемо:
 . (4.73)
. (4.73)
Формули (4.69) та (4.73) однакові за формою й мають назву – рівняння Даламбера.
Розв‘язок цього
рівняння є найлегшим для випадку
точкового заряду. За цих умов
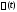 у сферичній системі координат не залежить
від кутів та визначається лише відстаннюr
від точкового заряду до точки спостереження
(для спрощення запису далі аргумент
у сферичній системі координат не залежить
від кутів та визначається лише відстаннюr
від точкового заряду до точки спостереження
(для спрощення запису далі аргумент
 не показуємо, наприклад
не показуємо, наприклад ).
).
Запишемо лапласіан у сферичній системи координат:
 .
.
Тобто з врахуванням
залежності від відстані r,
після диференціювання та перестановки
 :
:
 . (4.74)
. (4.74)
Тоді рівняння Даламбера:
 . (4.75)
. (4.75)
Перетворимо ліву
частину цього рівняння із введенням
нової змінної
 .
Диференціюванням заr
отримаємо:
.
Диференціюванням заr
отримаємо:

 (4.76)
(4.76)
та
 . (4.77)
. (4.77)
Підставимо (4.76) та
(4.77) у (4.75) з урахуванням
 ,
й отримаємо:
,
й отримаємо:
 . (4.78)
. (4.78)
формула (4.78) – хвильове рівняння (докладніше – див. розділ 6) – це неоднорідне диференціальне рівняння другого порядку в частинних похідних.
Нехай
 ,
тоді (4.78) трансформується в однорідне
рівняння:
,
тоді (4.78) трансформується в однорідне
рівняння:
 . (4.79)
. (4.79)
Формальним розв‘язком цього рівняння є:
 , (4.80)
, (4.80)
де
 – швидкість поширення електромагнітної
хвилі вздовж напряму
– швидкість поширення електромагнітної
хвилі вздовж напряму ;
для вільного простору
;
для вільного простору ;
; ,
, – деякі функції.
– деякі функції.
З урахуванням
заміни
 отримаємо
отримаємо
 . (4.81)
. (4.81)
Звідки маємо, що
аргументи функцій
 і
і відрізняються відносно аргументу
функції
відрізняються відносно аргументу
функції на значення
на значення .
.
Хвильові процеси
 і
і поширюються зі швидкістю v, абоc
– у вільному
просторі, в протилежних напрямах із
однаковими значеннями незалежно від
просторових кутів в усіх фіксованих
точках r.
поширюються зі швидкістю v, абоc
– у вільному
просторі, в протилежних напрямах із
однаковими значеннями незалежно від
просторових кутів в усіх фіксованих
точках r.
Таким чином, розв‘язок (4.81) описує дві сферичні хвилі, одна з яких «виходить» із випромінювача у нескінченність, а друга – «повертається». На рис. 4.5 обвідна другої хвилі показана як відбита (зворотна, або вторинна) від границі розподілу середовищ.

Рисунок 4.5. Обвідні прямої та відбитої хвиль
У нескінченому однорідному середовищі існують тільки хвилі, що поширюються від випромінювача, так звані «хвилі, що падають» (прямі, або первинні хвилі). Через це для подальшого аналізу залишимо перший доданок:
 , (4.82)
, (4.82)
де
 – поки ще невідома функція часу.
– поки ще невідома функція часу.
З електростатики відомо, що потенціал визначають як:
 . (4.83)
. (4.83)
Порівнюючи (4.82) і (4.83) одержимо, що одиниці вимірювання лівої та правої частин співпадають [В], якщо
 . (4.84)
. (4.84)
Тобто, це електричний потенціал змінного струму:
 (4.85)
(4.85)
Таким чином,
потенціал
 зареєстрований на відстаніr,
в момент часу t
визначають
значенням заряду q,
який передує спостереженню, тобто у
момент часу
зареєстрований на відстаніr,
в момент часу t
визначають
значенням заряду q,
який передує спостереженню, тобто у
момент часу
 .
Тому потенціал
.
Тому потенціал називаютьзатриманим
на
називаютьзатриманим
на
 .
Тобто «наслідок» затримано відносно
«причини», що збуджує процес.
.
Тобто «наслідок» затримано відносно
«причини», що збуджує процес.
Перейдемо від
точкового заряду до об’ємного з густиною
 .
.
Тоді електричний потенціал:
 , (4.86)
, (4.86)
де r
– відстань до точки спостереження
 .
.
Аналогічно для векторного магнітного потенціалу
 . (4.87)
. (4.87)
Для гармонічних процесів зручно користуватися комплексною формою функцій

У комплексній формі:
 ,
,
де
 – коефіцієнт фази, λ – довжина хвилі.
– коефіцієнт фази, λ – довжина хвилі.
У комплексній формі електричний затриманий потенціал, є таким:
 ,
(4.88)
,
(4.88)
– векторний магнітний затриманий потенціал, є таким:
 . (4.89)
. (4.89)
Множник
 –
характеризує затримання за часом
«наслідків» φ
та
–
характеризує затримання за часом
«наслідків» φ
та
 від «причин», відповідно
від «причин», відповідно та
та .
.
Таким чином, в динамічному режимі електричний та магнітний векторний потенціали є затриманими.
