4.5. Рівняння Максвелла для монохромного гармонічного коливання (у комплексній формі)

Для здійснення операцій з гармонічними функціями зручно користуватися навденням функцій у комплексній формі.

Нехай маємо гармонічну функцію:

. (4.34)

У цій формулі є три параметри: амплітуда – , частота –f (або кругова частота нагадаємо, що), початкова фаза –.

Звісно, виконувати операції з трьома параметрами складніше, ніж із меншою кількістю. Спробуємо зменшити кількість параметрів.

Скористаємося перетворенням Ейлера

. (4.35)

Якщо в (4.35) прийняти до уваги лише дійсний складник , то замість (4.34) можна записати

,

або , (4.36)

де – комплексна амплітуда .

У зв’язку з тим, що в лінійній системі кількість гармонічних складників не змінюється, можна вважати, що комплексна амплітуда є в площині, що «обертається» з круговою частотою ω, тобто для здійснення операцій достатньо мати комплексну амплітуду, яка містить інформацію лише за двома параметрами (амплітуда та початкова фаза). Окрім того, здійснювати математичні операції зручніше, якщо мати справу з експоненціальною функцією, показники якої додають або віднімають, замість операцій множення та ділення тригонометричних функцій, також легшими є операції диференціювання (інтегрування), для чого треба помножити (розділити) на jω.

Для повернення до миттєвих значень після операції з комплексною величиною достатньо визначити дійсну частину комплексної величини.

. (4.37)

Запишемо перше рівняння Максвелла, для гармонічного поля (4.19) (без сторонніх струмів) у комплексній формі:

. (4.38)

Скоротивши множники в рівнянні (4.38) маємо:

. (4.39)

Якщо винести за дужки загальний множник та , рівняння (4.39) матиме такий вигляд:

, (4.40)

де формула у дужках – це комплексна діелектрична проникність:

. (4.41)

Перевіримо одиницю вимірювання , тобто така ж, як для діелектричної проникності.

Формула (4.41) – має глибокий фізичний зміст – у ній є складник, який характеризує провідні властивості , та складник, який характеризує діелектричні властивості середовища й частота. Значення частотивпливає на співвідношення доданківта, тобто вона визначає співвідношення між значеннями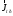та. А це свідчить про те, що за умов конкретних електродинамічних параметрів одне і теж середовище, залежно від частоти може характеризуватися різними властивостями, тобто бути провідним, діелектричним або напівпровідним (діелектриком з втратами) (див. підрозділ 4.6).

На підставі (4.36) за аналогією наведемо всі рівняння Максвелла у комплексній формі; для диференціальної форми – також із застосуванням оператора Гамільтона (набла) (табл. 4.3):

Таблиця 4.3. Система рівнянь Максвелла у комплексній формі

Рівняння Максвелла	Диференціальна форма	Інтегральна форма
перше	, або	,
друге	, , або	, ,
третє	, або	,
четверте	, або
п‘яте
шосте