4.2. Перше рівняння Максвелла (закон повного струму)

Перше рівняння Максвелла це закон повного струму:

, – диференціальна форма, (4.9)

– інтегральна форма. (4.9а)

Закон повного струму спочатку сформульовано за умови існування постійного струму провідності. Чи буде закон повного струму справедливий для змінного струму? Знайдемо дивергенцію від обох частин рівняння (4.9):

За визначенням, дивергенція ротора дорівнює нулю, тобто:

. (4.10)

Але з іншого боку, маємо для змінного струму (4.7), якщо йдеться про струм провідності:

. (4.11)

Тобто на підставі формули (4.11) можна зробити висновок, що рівність (4.9) коректна лише для постійного струму.

Щоб цю формулу можна було застосовувати для змінного струму треба здійснити корегування, яке реалізував Д. К. Максвелл. У праву частину (4.9) додамо деякий вектор , такий, що в результаті загальний вектор дорівнює ротору вектора напруженості магнітного поля:

. (4.12)

Виконаємо тепер ту саму операцію: визначимо дивергенцію від обох частин рівняння (4.12), та скористаємося тотожністю, що дивергенція ротора вектора напруженості магнітного поля дорівнює нулю:

. (4.13)

З формули (4.13) випливає, що

. (4.14)

Відповідно до закону збереження заряду з урахуванням (4.7), що й можливістю змінення порядку диференціювання формулу (4.14) можна переписати як:

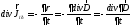. (4.15)

Звідки маємо

. (4.16)

Тобто одиниця вимірювання вектора [А/м²], й він дорівнює:

. (4.17)

Таким чином величину визначає похідна за часом вектора, і вона має назвувектор густини струму зміщення у діелектрику (введення поняття струм зміщення – велика заслуга Максвелла).

Остаточно, перше рівняння Максвелла у диференціальній формі записують так:

. (4.18)

Перепишемо рівняння (4.18) інакше:

(4.19)

де

, (4.20)

. (4.21)

Формула (4.20) є матеріальним рівнянням провідного середовища і описує закон Ома у диференціальній формі.

З рівняння (4.18) випливає, що магнітне поле створюють струм провідності та струм зміщення. Якщо середовище – ідеальний діелектрик, то струм провідності у ньому відсутній: . Тоді формула (4.19) набуває вигляд:

. (4.22)

Із формули (4.19) можна визначити, що вектори тавзаємно перпендикулярні. Векторитамають однаковий напрям, а будь-який вектор та вектор його ротора взаємно перпендикулярні. Додатково проілюструємо це на рис.4.2.

З використанням оператора Гамільтона (вектор – набла) операцію ротор записують:

. (4.23)

Відповідну графічну побудову стосовно (4.23) та (4.22) наведено на рис. 4.2, звідки випливає, що в однорідному просторі вектори тавзаємно перпендикулярні.

Рисунок 4.2. Визначення взаємної орієнтації у просторі векторів напруженості магнітного та електричного полів

Перше рівняння Максвелла у диференціальній формі описує зв’язок струму в конкретній точці з проекціями вектора . Для того, щоб отримати інтегральну форму, інтегруємо рівняння (4.18) за поверхнею та отримаємо:

. (4.24)

З використанням перетворення Стокса– формула (3.40) отримаємо:

. (4.25)

Рівняння (4.25) описує закон повного струму (в англомовній літературі – Ampere’s circuital law – круговий закон Ампера) в інтегральній формі – перше рівняння Максвелла в інтегральній формі: циркуляцію вектора напруженості магнітного поля за замкненим контуром визначає сума всіх струмів, які охоплені цим контуром, тобто струмів провідності тазміщення ; – удиференціальній формі – рівняння (4.18).