5. Енергія електромагнітного поля

5.1.Теорема Пойнтінга для миттєвих значень векторів поля

5.2. Теорема Пойнтінга для гармонічних процесів (у комплексній формі)

5.3. Уявлення процесу передавання енергії

5.4. Лема Лоренца

5.5. Висновки

5.6. Контрольні питання та завдання

В процесі роботи з матеріалом цього розділу та після його завершення, ви маєте

знати:

– обґрунтування теореми Пойнтінга;

– теорему Пойнтінга в диференціальній та інтегральній формах та їх сутність;

– сутність балансу потужностей;

– теорему Пойнтінга у комплексній формі та сутність її складників;

– дійсний складник вектора Пойнтінга (середнє значення) та уявний складник (змінний подвійної частоти);

– формули для енергії електромагнітного поля;

– принцип процесу перенесення енергії провідниками зі струмом;

– зв’язок між двома сторонніми струмами у двох різних точках простору і електромагнітними полями, які збуджені цими джерелами (лема Лоренца);

– напрям якого процесу характеризує вектор Пойнтінга;

вміти:

– вивести теорему Пойнтінга;

– обчислювати складники теореми Пойнтінга;

– обчислювати складники вектора Пойнтінга в комплексній формі;

– обчислювати потужність електромагнітного поля;

– розв’язувати задачі на основі теореми Пойнтінга;

– описати принцип процесу перенесення енергії провідниками зі струмом;

– отримати співвідношення леми Лоренца;

– визначити напрям вектора Пойнтінга стосовно векторів та

5.1. Теорема Пойнтінга для миттєвих значень векторів поля

У 1874 р. російський фізик Н. А. Умов запропонував та обґрунтував поняття густини потоку енергії стосовно механіки й довів, що перерозподіл енергії в просторі здійснено в результаті її перенесення з одних областей поля в інші.

У 1884 р. англійський фізик Дж. Пойнтінг запропонував та обґрунтував поняття густини потоку енергії електромагнітного поля.

Нехай у будь-якому обмеженому об’ємі з врахуванням втрат, які обумовлені електричною та умовною магнітною питомими провідностями,є стороннє джерело електромагнітного поля, визначене векторами густини електричного та умовного магнітногострумів (рис. 5.1). З’ясуємо, яким чином розподілено енергію цього джерела в даному об’ємі та за його межами.

Рисунок 5.1. Об’єм V, обмежений поверхнею, із джерелом та складниками електромагнітного поля

Зауважимо, що в природі магнітний струм не існує, проте задля одержання чіткої системи всіх складників балансу потужності електромагнітного поля запишемо перше та друге рівняння Максвелла у диференціальній формі у повному складі, тобто з врахуванням сторонніх струмів (електричного й магнітного ), електричних та магнітних втрат, обумовлених наявністюта(див. табл. 4.2):

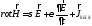,(5.1)

.(5.2)

Помножимо скалярно ці рівняння: перше на , друге на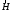та віднімемо (5.1) від (5.2):

. (5.3)

На підставі тотожності векторного аналізу:

та перегрупування складників з (5.3) маємо:

. (5.4)

Рівняння (5.4) – теорема Пойнтінга у диференціальній формі (для миттєвих значень векторів). Усі складники характеризують густину потужності.

Звернемо увагу на перший доданок лівої частини під знаком дивергенції: маємо векторний добуток, який називають вектор Пойнтінга, що визначає густину потужності:

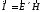. (5.5)

Проінтегруємо (5.4) за об’ємом:

(5.6)

Формула (5.6) є теоремою Пойнтінга в інтегральній формі. Після перегрупування доданків і використання перетворення (теореми) Гаусса-Остроградського відносно першого доданка маємо:

(5.7)

.

Визначимо чотири типи доданків:

;– перша група;

;– друга група;

;– третя група;

– особливий доданок.

Визначимо фізичний зміст всіх доданків.

Перша група характеризує потужність сторонніх джерел електричного та магнітного, відповідно:

, (5.8)

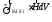. (5.8а)

Друга група характеризує теплові втрати потужності, які зосереджені в об’ємі,а саме електричні та магнітні відповідно:

, (5.9)

(5.9а)

Третя група характеризує потужності електричного та магнітного полів, які зосереджені в об’ємі , тобто потужності, що витрачені на утворення відповідних складників електромагнітного поля:

, (5.10)

. (5.10а)

Останній доданок – дуже важливий для практики електрозв’язку. Це потужність електромагнітного поля крізь замкнену поверхню , яка охоплює об’єм, в якому зосереджено сторонні джерела поля. Цей доданок надає можливість використовувати мобільний зв’язок, переглядати телевізійні передачі, слухати радіо та ін., тобто це –потужність емісії електромагнітного поля – носія інформації:

. (5.11)

Таким чином у формулі (5.7) є:

– потужність сторонніх джерел поля – перша група (5.8), (5.8а);

– потужність втрат – друга група (5.9), (5.9а);

– потужність електричного та магнітного полів, зосереджену в даному об’ємі 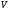– третя група (5.10), (5.10а);

– потужність електромагнітного поля (5.11), яка «виходить» за межі цього об’єму.

Сума цих потужностей дорівнює нулю, що свідчить про баланс миттєвої потужності в просторі.

Теорема Пойнтінга – одне з найважливіших положень електродинаміки, на основі якого далі отримано формулу ідеального радіозв’язку. Якщо відоме значення вектора Пойнтінга, можна визначити потужність, яку випромінюють та приймають антени, розрахувати потужність, яка поширюється у хвилеводах тощо.

Визначимо складник електричної енергії електромагнітного поля в об’ємі. Для цього проінтегруємо (5.10) за часом:

. (5.12)

Після визначення як повного диференціала, запишемо (5.12) у формі:

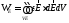. (5.13)

Після інтегрування за напруженістю електричного поля, маємо

. (5.14)

Після виконання аналогічної процедури з (5.10а), отримаємо:

. (5.15)

У формулах (5.14) та (5.15) під інтегралами є, відповідно, густина енергії електричного та магнітних полів:

, (5.16)

. (5.17)

Енергію електромагнітного поля визначимо як суму складників (5.14) та (5.15)

. (5.18)

Для практики електрозв’язку дуже важливим є визначення напряму вектора Пойнтінга.

Зорієнтуємо в декартовій системі координат вектори іта за правилом векторного множення визначимо напрям вектора(рис. 5.2).

Площина, в якій розташовано вектори імає назвуфронт електромагнітної хвилі. Таким чином вектор Пойнтінга зорієнтовано перпендикулярно до фронту електромагнітної хвилі.

Рисунок 5.2. Визначення напрямку вектора Пойнтінга