10.2. Поширення радіохвиль у вільному просторі. Формула ідеального радіозв’язку

Для початку з’ясуємо особливості процесу поширення радіохвиль у вакуумі з параметрами: . Стосовно поширення радіохвиль застосовують модель вільного простору, параметри якого вважають близькими до вакууму. Отримані для цієї ситуації формули є базовими, на підставі яких створено теоретичну базу процесу поширення радіохвиль.

Поширення радіохвиль в реальних умовах характеризують аналогічними формулами із введенням корегувальних коефіцієнтів.

Отримаємо формули ідеального радіозв’язку:

Застосуємо спочатку модель ізотропної антени, яка випромінює радіохвилю з частотою-носієм , потужністюв точці А,однаково в усі сторони – рис. 10.4.

Для ізотропної антени енергія радіохвилі розподілена рівномірно на поверхні уявної сфери і визначає потужність випромінювання.

Фізик Джон Генрі Пойнтинг (1852–1914) вперше отримав формулу для густини потужності, що переносить електромагнітне поле (вектор Пойнтинга – див. розділ 5).

Рисунок 10.4. Модель ізотропного випромінювача

Потужність проміння у будь-якій точці зони поширення радіохвиль можна визначити інтегруванням за поверхнею вектора Пойнтинга:

, (10.1)

де – вектор Пойнтинга,– площа сфери.

Для сфери значення модуля вектора Пойнтинга дорівнює:

. (10.1а)

Вектор є векторним добутком напруженості електричного та магнітного полівта, які в просторі взаємно перпендикулярні, в дальній зоні змінюються синфазно, його напрям визначає напрям поширення електромагнітної хвилі, тому модуль:

, (10.1б)

де та– амплітудні значення складників напруженості електричного та магнітного полів ().

Скористаймось поняттям хвильового опору, що є коефіцієнтом пропорційності між таудальній зоні (6.28):

.

Для вільного простору Ом.

Із (10.1б) та співвідношення запишемо середньоквадратичне значення вектора Пойнтинга:

. (10.2)

Тоді з (10.2) з урахуванням (10.1а) отримаємо амплітудне та середньоквадратичне значення напруженості поля, відповідно:

; (10.3)

. (10.3а)

Цю залежність значення напруженості поля від потужності випромінювання та відстані називають формулою ідеального радіозв’язку.

Для практичного застосування використовують одиниці вимірювання для потужності – кіловати, а для відстані – кілометри, вони є більш зручні для реальних умов. За їх застосування формули (10.3) та (10.3а) такі:

, (10.3б)

. (10.3в)

Ізотропні випромінювачі – це ідеальні випромінювачі, їх неможливо реалізувати на практиці. Навіть диполь Герца – елементарний випромінювач, має спрямувальні властивості (див 7.9). Реально застосовують антени, що мають діаграму спрямованості, тобто різний розподіл випромінення у різних напрямах, наприклад, рис. 10.5.

Рисунок 10.5. Приклад діаграми спрямованості антени

Більш докладно щодо спрямованості та параметрів антен наведено в кредитному модулі «Технічна електродинаміка та поширення радіохвиль – 2».

Ступінь концентрації потужності випромінювання визначає коефіцієнт спрямованої дії антени – . Спрямована антена, що випромінює потужність , створює таку ж напруженість поля, як ізотропна антена, що випромінює потужність більшу вразів. Тобто застосування спрямованих антен дозволяє зменшити випромінювальну потужність передавачавразів, й тоді замість (10.3) маємо:

. (10.4)

Із урахуванням діаграми спрямованості антен напруженість поля визначають у сферичній системі координат – , тобто залежно від просторових кутіввертикальної (меридіальної) та горизонтальної (азимутальної) площин відповідно. Максимальну напруженість поля, створюваного реальною антеною записують, як.

Нормовану (відносно максимального значення) характеристику спрямованості антени визначають як:

. (10.5)

Миттєве значення напруженості поля описують формулою (6.22) (як розв’язок хвильового рівняння (6.9)):

.

Із застосуванням (10.4) та (10.5) за умови, що початкова фаза дорівнює нулю маємо для прямої хвилі:

(10.6)

де – відповідно коефіцієнтизгасання та фази.

З урахуванням (10.4), маємо:

. (10.6а)

У комплексній формі:

. (10.6б)

Ці формули актуальні для антен будь-якого типу за умов відповідних значень множника .

Протягом довгого часу процес поширення радіохвиль оцінювали значенням величини E, що створює передавач у місці приймання. Такий критерій був доцільний для зв’язку у діапазонах ДНЧ (3-30 кГц), тобто дуже довгих хвиль (100-10 км); НЧ (30-300 кГц) – довгих хвиль (10-1 км); СЧ (300-3000 кГц) – середніх хвиль (1000-100 м) та ВЧ (3-30 МГц) – діапазон коротких хвиль (100-10 м). Внаслідок широкого застосування хвиль більш високих частот сигнал доцільно характеризувати потужністю, на вході приймача (), бочутливість приймальних приладів також визначають потужністю, необхідною для приймання сигналу:

(10.7)

де – ефективна площа антени, її можна трактувати як частину площі фронту радіохвилі, яка віддає енергію антені:

(10.8)

де – коефіцієнт спрямованої дії приймальної антени.

За формулами (10.7), (10.8), (10.1а) з урахуванням коефіцієнта спрямованої дії передавальної антени отримуємо:

. (10.9)

Формулу ідеального радіозв’язку в такої формі також називають формулою Фріїса (Friis).

Співвідношення, яке характеризує послаблення потужності за умови поширення радіохвиль у вільному просторі (якщо ), має назвувтрати у вільному просторі:

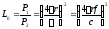, (10.10)

де – значення відоме, як швидкість світла (в даному випадку швидкість поширення електромагнітної хвилі) у вакуумі (вільному просторі).

Втрати під час поширення електромагнітних хвиль з урахуванням коефіцієнтів спрямованої дії передавача та приймачаназивають основними втратами:

. (10.10а)

Застосовують також обернену величину:

, (10.11)

або у відносних одиницях:

(10.11а)

де – відстань відносно 1км,– частота відносно 1МГц,.

Із урахуванням значень с та – отримаємо:

дБ. (10.11б)

У зв’язку з тим, що значення тавідрізняються на декілька порядків, для полегшення розрахунків, доцільно застосовувати значення потужності у логарифмічних одиницях –децибелах:

, (10.12)

за опорний рівень прийнято, або

, (10.12а)

за опорний рівень прийнято .

Зазначимо, що рівень Р_дБм=Р_дБ+30, або 0 дБ=30 дБ, 0 дБм=30 дБ. Акцентуємо також увагу на те, що аналогічні формули для напруженості поля мають інший вигляд: (де), бо.

На рисунку 10.6 наведено залежності від відстані та частоти:

a

б

Рисунок 10.6. Залежності від відстані та частоти для відносних шкал:а – стосовно 1 Вт (дБ), б – 1 мВт (дБм)

З’ясуємо далі, як виникають додаткові втрати.