Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный технический университет Украины «Киевский политехнический институт»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

attachment

.pdf

Скачиваний:

Добавлен:

12.05.2015

Размер:

3.12 Mб

Скачать

☆

<<< < Предыдущая 12 / 162 3 4 5 6 7 8 9 10 11 12 13 14 15 16 > Следующая >>>


lim	r	1,

	S
S 0

	MM / (рис.1.7).
оскільки r є довжина хорди

На підставі викладеного дістанемо

		dS	(1.20)
		dt

Щоб визначити dSdt , домножимо рівність (1.20) скалярно на орт .

dS	;	dS	(1.21)

dt		dt

Отже, dSdt є проекція швидкості на дотичну до траєкторії. Таким чином,

(1.22)

Рівності (1.20) – (1.22) визначають вектор швидкості точки натуральним способом математичного опису її руху.

1.1.5. Прискорення руху точки

Прискорення є фізична величина, що характеризує бистроту зміни швидкості руху точки за часом.

На підставі цього означення і змісту підрозд. 1.1.3 можна визначити величину і

напрям прискорення точки:
W	d	(1.23)
	dt


Вектор W напрямлений по дотичній до		годографа вектора швидкості

.Знайдемо прискорення точки трьома способами опису її руху.


Якщо рух точки задано	векторним				рівнянням		r	r (t) , то швидкість
d r dt , а на підставі (1.23) прискорення
			d			d 2 r	..
W lim			d			d 2 r	r	(1.24)
W lim							r	(1.24)

t t			dt			dt2
Для визначення прискорення точки координатним способом скористаємось
рівностями (1.7) і (1.24):
		..		..	..
W i x j y k z								(a)

Розкладаючи вектор прискорення W по ортах декартової системи координат
W iWx jWy					kWz			(b)

і порівнюючи вирази (а) і (b) маємо
Wx x ; Wy	y ;	Wz z	(1.25)

Отже, проекції вектора прискорення на координатні осі дорівнюють першим похідним за часом відповідних проекцій швидкості за часом, або другим похідним

відповідних координат рухомої точки за часом.

Модуль вектора W і			його	напрямні косинуси знаходимо за				відповідними
формулами аналітичної геометрії:

			W		x2 y2 z2			(1.26)
cos(W , ^ Ox)	W	x	; cos(W , ^ Oy )			Wy	; cos(W , ^ Oz)	W
cos(W , ^ Ox)		x	; cos(W , ^ Oy )				; cos(W , ^ Oz)		z	(1.27)
	W					W			W

Формули (1.25) – (1.27) визначають вектор прискорення координатним способом.

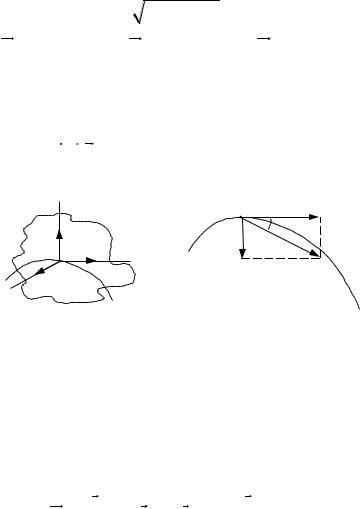
Натуральні осі та натуральний тригранник. Кінематичні характеристики руху точки тісно пов’язані з геометричними властивостями траєкторії. Як відомо з диференціальної геометрії, у кожній точці кривої є три взаємно перпендикулярні напрямки: дотична, головна нормаль і бінормаль, одиничні вектори (або орти) які

позначимо відповідно , n, b.

Побудуємо місцевий координатний базис – натуральний тріедр (рис. 1.8). Орти дотичної і головної нормалі створюють стичну площину кривої.

	M
	M	w
		α

M
	wn
n	wn
n
рис. 1.8		рис. 1.9

Проведемо нормаль до цієї площини. Цю нормаль називають бінормаллю, її орт. У площині ( , n) розміщені всі нормалі до кривої, тому орти ( , n) створюють

нормальну площину кривої. Орти ( , ) створюють спрямляючу площину кривої. Орти

( , n) створюють стичну площину.

Прискорення точки при натуральному способі задання руху визначається за такою теоремою.

Теорема. Повне прискорення точки дорівнює векторній сумі дотичного (тангенціального) та нормального прискорень.

Доведення. Нехай рух точки задано натуральним способом. Із (1.22) і (1.23) дістанемо

W	d	d	( )	d	d	.	(с)
	dt	dt		dt	dt

Перший доданок називається дотичною, або тангенціальною складовою

прискорення і позначається W . Отже,

W d d 2s s dt dt2

З цього рівняння випливає, що дотичне прискорення характеризує зміну швидкості за величиною і дорівнює першій похідній за часом від проекції швидкості на

дотичну або другій похідній від дугової координати за часом.

Зауважимо, що орт

змінює свій напрям зі зміною дугової координати S , тобто

його можна розглядати як складну функцію часу S(t) . Отже, другий доданок

можна подати у вигляді:

d [S (t)]

d dS

(S )

(d)

dS dt

S :

Візьмемо похідну від

за

(e)

1 та продиференціюємо її по S.

Розглянемо тотожність 2

Тоді одержимо:

d ( )

а)

Із цього випливає,

що

вектори

і -

перпендикулярні (рис.1.10);

б) вектор завжди напрямлений у бік угнутості траєкторії.

в) вектор		лежить у стичній площині;
	S


Вектор	d dS		напрямлений,		як		N
							N
відомо, по дотичній до годографа вектора

. Оскільки	- одиничний вектор, його					M			s
годограф є крива, розміщена				на поверхні				K	s	M'
сфери одиничного радіуса. Тому вектор								K		M'
сфери одиничного радіуса. Тому вектор
утворює з вектором			dS	прямий	кут
утворює з вектором		d	dS	прямий	кут
(рис.1.10). З’ясуємо,		вздовж		якої нормалі			d
			dS . Для цього				d s
напрямлений	вектор	d	dS . Для цього				d s

розглянемо граничний напрям вектора .							рис. 1.10

Щоб його побудувати, проведемо одиничні

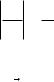
		в сусідніх точках M і	M / , де MM / S . Побудуємо в
вектори	і	в сусідніх точках M і	M / , де MM / S . Побудуємо в

точці M вектор MK , що дорівнює			. Тоді NK .

Якщо S прямує до нуля, точка M / прямує M , прямує до нуля, то

площина трикутника MNK , обертаючись навколо нерухомого вектора , наближається до певного граничного положення. Це граничне положення площини трикутника MNK знаходиться в стичній площині кривої в точці M . Отже, нормаль,

вздовж якої напрямлений вектор d dS , лежить в стичній площині.

Зауважимо, що всяка плоска крива всіма точками лежить у стичній площині.

З рис. 1.10 видно, що вектор d dS напрямлений у бік угнутості кривої, тобто в бік її центра кривизни траєкторії.

Визначимо модуль вектора d 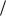dS :

lim

S 0

З рис. 1.10 знаходимо

2sin

тому

2 sin

sin

lim

S 0

Оскільки

lim

sin 2

1 ;

lim

де - радіус кривизни кривої , то

d 1 dS

Позначимо одиничний орт головної нормалі через n угнутості кривої. Тоді

	d
			n
	dS

На підставі (d) і ( j ) вираз (c) набуває вигляду

(i)

напрямимо його в бік

(j)

W	d	n	2
			.	(1.28)

	dt

Зауважимо, що 2	2 , де модуль швидкості.

Розкладемо вектор W по ортах натурального тріедра:

W W nWn W (1.29)

і порівняємо здобутий вираз із формулою (1.28):

W	d	d 2S	; Wn	2
					.	(1.30)
	dt	dt2

Як видно з (1.29), (1.30), проекція вектора прискорення на бінормаль дорівнює

нулеві.

Отже, вектор прискорення точки лежить завжди у стичній площині траєкторії точки. Проекцією W називають дотичним, або тангенціальним прискоренням,

проекцію Wn - доцентровим, або нормальним прискоренням.

Повне прискорення точки є векторна сума дотичного і нормального прискорень

(рис.1.9).

Із (1.30) витікає очевидний фізичний зміст складових прискорення: тангенціальне прискорення характеризує зміну швидкості за величиною, нормальне – за напрямом.

Дійсно, якщо точка рухається рівномірно ( const ), то W =0. Якщо траєкторія

точки – пряма лінія, то = і Wn =0.
Таким чином, модуль прискорення і його напрям знаходяться із виразів:
		; tg	Wn	.
W W 2	W 2		Wn		(1.31)
W W 2	W 2				(1.31)
	n	W
		W

Отже, формули (1.28), (1.30), (1.31) визначають вектор прискорення натуральним способом.

Приклади

1.Рівнозмінний рух точки.

Рух точки називається рівнозмінним, якщо її дотичне прискорення стале ( W =а).

Знайдемо швидкість точки і закон її руху по траєкторії. На підставі (1.30)

d a ; d adt dt

звідки

at C1 .

За формулою (1.21)

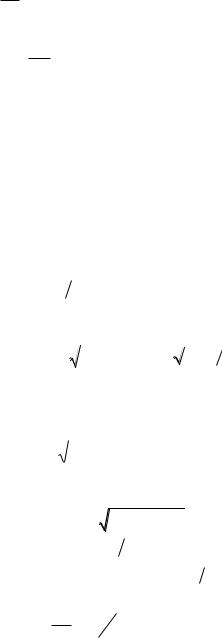
dSdt ; dS dt ,

звідки після інтегрування маємо

S at2 C1t C2 ,

де C1 і C2 - сталі інтегрування, що знаходяться з початкових умов. У даному

випадку початковими умовами є початкова швидкість і початкова дугова координата. Нехай

t 0 0 ;

t 0 S0

Дістанемо ,

t ;

(1.32)

S S0

(1.33)

2. Рух точки визначається рівняннями x 2cos4t ,

y 2sin 4t ,

z 2t

( x, y, z - у метрах, t - в секундах ). Визначити радіус кривизни траєкторії точки.

На підставі (1.30) знаходимо 2

. Отже, треба обчислити 2 і

W .

З рівнянь руху маємо

x x 8sin 4t ;

68 м с ;

y y 8cos 4t ;

z 2 .

Швидкість точки – стала величина .

Нормальне прискорення визначимо через повне і тангенціальне за формулами

(1.30) і (1.31) :


	W			W 2 W 2 .
	n
Повне прискорення
	Wx	x 32 cos 4t ;
	32 sin 4t		; W
					2	2	2	;
Wy y					x	y	z	;
	W z 0 ; W 32 м с2
	z
Оскільки V const , а W V			0 , то W W 32 м с2 .
					n

Знаходимо

V 2 2 18 м

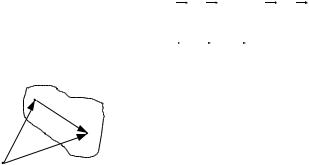
3. Рух точки відбувається за законом x 1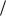3t 2 1 ; y 2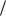3t 2 .

Визначити швидкість , прискорення точки, радіус кривизни траєкторії і закон руху точки по траєкторії.

Відповідь:

4. В певний момент часу повне прискорення точки дорівнює 2,6 м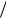с2 . Точка

рухається по кривій з дотичним прискоренням 1,4 м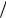с2 . Знайти для даного моменту часу нормальне прискорення точки.

Відповідь: W 2,2 м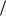с .

1.2.Основи кінематики твердого тіла

1.2.1. Основні положення

Основне завдання кінематики твердого тіла – визначення закону руху і основних характеристик руху – швидкості та прискорення. На відміну від однієї точки при вивченні руху твердого тіла розглядатимемо як характеристики руху всього тіла в цілому, так і характеристики руху окремих точок тіла.

До найпростіших рухів твердого тіла належать: поступальний рух і обертальний навколо нерухомої осі . Далі покажемо, що будь-які складні рухи твердого тіла можна розкласти на поступальний і обертальний рух навколо осі.

1.2.2. Поступальний рух твердого тіла

Поступальним називають такий рух твердого тіла, при якому довільна пряма, проведена в тілі, рухається паралельно сама собі.

Для дослідження поступального руху твердого тіла доведемо наступну теорему.

Теорема. При поступальному русі твердого тіла всі точки тіла рухаються з однаковими швидкостями й прискореннями.

Розглянемо	в тілі дві довільні точки A і B		і визначимо їх рух векторним
способом :
		rA rA (t) ,	rB rB (t)
На підставі рис.1.11 маємо
		rB rA rAB	(1.34)
A		Функції rA (t) і rB (t) визначають векторним
A		способом траєкторії точок	A та B .
rAB
	B	Вектор rAB не змінюється за величиною і напрямом з
rA	B	часом. Отже, із (1.34) видно, що траєкторію точки A можна
		часом. Отже, із (1.34) видно, що траєкторію точки A можна
		дістати з траєкторії точки	B за допомогою паралельного
rB
O		переносу. Напрям і величину переносу визначав вектор rAB .
Рис. 1.11			17

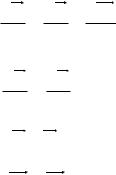
Знайдемо похідну від виразу (1.34):

d rB d rA d rAB dt dt dt

Вектор rAB = const , тому

d rB d rA dt dt

тобто

B A .

(1.35)

Диференціюючи (1.35) за часом, дістаємо

WB WA

(1.36)

На підставі доведеної теореми можна стверджувати, що поступальний рух повністю визначається рухом однієї довільної точки тіла. Отже, вивчення поступального руху тіла безпосередньо пов’язане з кінематикою точки.

1.2.3. Обертальний рух твердого тіла навколо нерухомої осі

Обертальним рухом тіла навколо нерухомої осі називають рух твердого тіла, при якому певна пряма (вісь обертання), що проходить через які-небудь дві точки під час руху тіла залишається нерухомою.

Визначимо закон обертального руху тіла навколо осі. Нехай вісь Oz , рис.(1.12) є нерухома вісь,навколо якої обертається тіло. Проведемо через вісь Oz у деякий початковий момент часу t0 площину P0 .

Через деякий проміжок часу ця площина займе положення P , створивши двогранний кут зі своїм початковим положенням. Цей двогранний кут називається кутом повороту і виміряється лінійним кутом .

Oz , і в протилежному

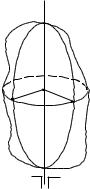
Вважатимемо кут повороту	додатним,	якщо з боку
додатного напряму осі Oz цей
	поворот видно	проти ходу
годинникової стрілки.			z
Кожному моментові часу t	відповідає повне значення
кута повороту . Отже, кут повороту є функція часу:

(t)	(1.37)	PO	P
Це рівняння називається кінематичним рівнянням			O
обертального руху тіла навколо нерухомої осі.			φ
З кутом повороту пов’язані дві основні кінематичні		MO	M

величини, що характеризують обертальний рух твердого тіла: кутова швидкість і кутове прискорення.

Кутовою швидкістю тіла називають фізичну величину, що характеризує бистроту зміни кута повороту тіла у часі.

	На підставі попередніх міркувань
	На підставі попередніх міркувань						Рис. 1.12
		d			рад		Рис. 1.12
		d			рад
						.	(1.38)
						.	(1.38)
		dt			с
	Отже, кутова швидкість дорівнює першій похідній за часом від кута повороту .
між	У техніці кутову швидкість часто задають числом n обертів за хвилину. Зв’язок
між	та n визначається формулою
			2 n		n .
					n .
				60	30
	Кутова швидкість визначає також і напрям обертання. Так, якщо >0, то тіло в

даний момент обертається в напрямі зростання кута повороту – проти ходу годинникової стрілки, якщо дивитися з боку вибраного додатного напряму осі напрямі, якщо < 0.

Кутовим прискоренням називають фізичну величину, що визначає бистроту зміни кутової швидкості в часі. Кутове прискорення можна знайти, якщо продиференціювати за часом кутову швидкість:

рад		(1.39)
с	2

Якщо знаки і збігаються, то кутова швидкість зростає, обертання

прискорене.
	Наведені формули визначають і як скалярні величини. Зауважимо, що і
	однакові для всіх точок тіла.

Розглянемо розподіл лінійних швидкостей у тілі, що обертається навколо осі. Скористаємося натуральним способом визначення руху точки і розглянемо рух довільної

точки M тіла. Якщо початкове положення точки M 0 відповідає початковому значенню кута повороту , то на підставі (1.31) маємо:

M 0 M S R (t) ,

де R - відстань від точки M до нерухомої осі.

S - дугова координата, що відповідає куту повороту .

Це рівняння є закон руху точки по траєкторії.

Щоб знайти проекцію швидкості точки M на дотичну, продиференціюємо його за часом:

(R (t)) R

R ,

(1.40)

або

R R .

Отже, лінійні швидкості залежно від радіуса розподіляються за лінійним законом

(рис.1.13).

Щоб знайти розподіл лінійних прискорень, скористаємось формулами (1.30) і

(1.40).

Дістанемо

W R

R ;

W 2

2 R

(1.41)

Модуль прискорення знайдемо за формулою:

W 2 W 2 ; W R 2 4 .

(1.43)

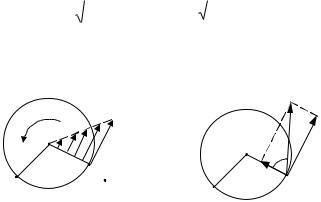
Кут між вектором повного прискорення і радіусом обертання (рис.1.14):

(1.44)


O				w
O		O
φ		O	wn	α
φ	M		φ	α
	M		φ	M
M				M
M		M
		M
Рис. 1.13		Рис. 1.14
Оскільки і не залежать від положення точки M , то кут однаковий для
всіх точок тіла.

1.2.4. Вектори кутової швидкості і кутового прискорення. Формула Ейлера

Узагальнимо поняття про кутову швидкість тіла, що обертається навколо осі. Виберемо початок прямокутної декартової системи координат на осі обертання

(рис.1.15) і вважатимемо, що вона незмінно зв’язана з тілом і обертається разом з ним.

Орт k	лежить на нерухомій осі Oz , орти i	і j , зберігаючи модуль, змінюють

напрям.

Визначимо швидкість довільної точки М тіла. На підставі (1.15)

<<< < Предыдущая 12 / 162 3 4 5 6 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.03.2016393.9 Кб10ASSUD_Orda_4ASU-A.docx
#
23.11.2019349.7 Кб6ASS_1nn.doc
#
17.03.20161.07 Mб6atp_shemu_1354515770.pdf
#
21.11.2018404.48 Кб2attachment.doc
#
15.04.2019617.47 Кб1attachment.doc
#
12.05.20153.12 Mб13attachment.pdf
#
15.04.2019250.88 Кб1attachment1.doc
#
12.05.20152.01 Mб72AutoCAD.pdf
#
17.03.20161.97 Mб32A_S_Makarenko_Pedagogicheskaya_poema МАКАРЕНКО ПЕДАГОГИЧЕСКАЯ ПОЭМА.pdf
#
17.03.20161.59 Mб24b.pdf
#
17.03.2016146.43 Кб6bakalavr_diploma2012.doc