
attachment
.pdf
і називається загальним рівнянням статики. Цей термін можна пояснити тим, що з нього легко дістати умови рівноваги вільного твердого тіла і всі можливі умови рівноваги системи тіл.
Розглянемо вільне тверде тіло (рис.3.7),
|
|
F1 |
на яке діють сили F1, F2 ,....,Fn . |
Якщо тіло |
|||
|
|
||||||
|
|
|
|||||
|
|
|
невільне, скористаємось аксіомою про |
||||
|
|
|
звільнення від в’язей і реакції в’язей |
||||
|
|
|
приєднаємо до активних сил. |
|
|||
|
|
|
Надамо тілу |
певного можливого |
|||
|
|
|
переміщення і обчислимо елементарну роботу |
||||
F i |
|
всіх діючих сил на цьому переміщенні. Згідно |
|||||
F n |
з теоремою про роботу сил, що |
діють на |
|||||
|
|
||||||
рис. 3.7 |
|
абсолютно |
тверде тіло, |
ця робота дорівнює |
|||
|
роботі, виконаній головним вектором системи |
||||||
|
|
|
|||||
сил на переміщенні полюса, і роботі головного моменту |
відносно полюса на |
||||||
обертальному переміщенні навколо полюса: |
|
|
|
||||
|
|
A R r0 M 0 . |
|
(c) |
|||
Полюс беремо в довільній точці О. На підставі (3.5) вираз (c) набуває |
|||||||
вигляду |
|
|
|
|
|
||
|
|
R r0 M 0 0 |
|
(d) |
|||
Можливе переміщення полюса r 0 |
і обертальне переміщення навколо |
||||||
полюса - незалежні. Нехай =0, r0 |
0 . |
|
|
||||
Тоді з (m) маємо R r0 |
0 . |
|
|
|
|||
Ця умова здійснюється для всіх довільних r 0 лише тоді, коли |
|
||||||
|
|
|
R 0 . |
|
|
(e) |
|
Аналогічно можна довести , що |
|
|
|
||||
|
|
|
M 0. |
|
|
(f) |
|
Рівності (e) та (f) – відомі умови рівноваги вільного твердого тіла. Аналогічно можна знайти умови рівноваги невільного твердого тіла.
Розглянемо, наприклад, тверде тіло, що має дві нерухомі точки, нерухому вісь.
Візьмемо полюс на цій осі. Тоді r 0 =0, а k , де k - орт осі обертання. Рівняння (d) набуває вигляду
M 0 k 0 . |
(g) |
Співвідношення (g) повинно бути справедливим при довільному .
Отже,
M 0 k M2 0 |
(h) |
81

Рівність (h) – відома умова рівноваги тіла з нерухомою віссю.
3.4. Принцип Даламбера-Лагранжа. Загальне рівняння динаміки
Принцип Даламбера дає можливість поширити принцип можливих переміщень на випадок руху системи. Дійсно, якщо до точок системи прикласти сили інерції, то можна вважати, що система перебуває у стані рівноваги. Тоді можна застосувати принцип можливих переміщень. У результаті дістанемо принцип Даламбера-Лагранжа.
Якщо на систему накладено ідеальні в’язі, то сума робіт активних сил і сил інерції на можливих переміщеннях точок системи буде від’ємною або дорівнюватиме нулю:
n |
|
|
|
|
|
F i |
miW i ri |
0. |
(3.6) |
||
i 1 |
|
|
|
|
|
Як і раніше, знак нерівності стосується можливих переміщень, що |
|||||
зводять точки системи з однобічних в’язей. |
|
|
|
||
При відсутності однобічних в’язей із нерівності (3.6) дістанемо рівність, |
|||||
яка називається загальним рівнянням динаміки: |
|
||||
n |
|
|
|
|
|
F i |
miW i ri |
0. |
(3.7) |
||
i 1
Впроваджений термін пояснюється тим, що з цього рівняння, як наслідок, випливають основні рівняння руху системи, а також основні теореми динаміки.
Приклади
1. Балка АВ (рис.3.8) спирається в точках А та В на шарнірно-рухому і
шарнірно-нерухому опори і знаходиться під дією двох сил ( P і Q ),
прикладених в точках С і D(AC=CD=DB=a). Кут відомий. Користуючись загальним рівнянням статики, визначити реакцію опори В.
Скористаємось аксіомою про звільнення від в’язей і прикладемо в точці силу В, яку приєднаємо до вже відомих активних сил. Розглянемо балку АВ як систему з ідеальними двобічними в’язями. Надамо точкам системи можливих
переміщень: r1 , r 2 , r B . Застосовуючи загальне рівняння статики (4.3), дістанемо
P r1 Q r2 RB rB 0 |
(а) |
|
або |
|
|
P sin r1 Q r2 RB rB 0 |
(b) |
|
Встановимо зв’язок між |
r1 , r 2 , r B . Елементарні |
геометричні |
обчислення дають змогу знайти |
|
|
r B 3 r1 ; |
r2 2 r1 . |
|
Тоді вираз (b) запишеться у вигляді
82

Psin r1 Q 2 r1 RB 3 r1 0
Після очевидних спрощень знайдемо
RB 13 (P sin 2Q)
2. На подвійному блоці знаходяться ланцюги, які підтримують тягарі M1 і M2 (рис.3.3). Знайти кутове прискорення блока, нехтуючи його масою і
масами ланцюгів, якщо вага тягарів відповідно P і |
P . |
||||||
|
|
|
|
|
|
1 |
2 |
Припустимо, |
що |
P |
> P . |
Напрями прискорень тягарів дають змогу |
|||
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
||
визначити напрями |
сил |
інерції |
1 і |
2 .Надамо |
точкам системи можливих |
||
|
|
|
|
|
|
|
|
переміщень s1 |
, s2 |
і скористаємося загальним рівнянням динаміки |
|||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
F i |
i ri |
|
0 |
|
|
|
|||||||||||||
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P s |
2 |
s P s s 0 |
(с) |
|||||||||||||||||
2 |
2 |
|
|
|
2 |
1 |
|
1 |
|
|
|
1 |
|
|
1 |
|
||||
Залежність між s1 |
і s2 |
|
така : |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
s1 r1 ; |
|
s2 r2 . |
|
|
(d) |
||||||||||||||
Сили інерції |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m W |
|
P |
|
r |
|
|
|
|
|
P |
r . |
|
||||||||
|
1 |
|
; |
|
|
2 |
|
(е) |
||||||||||||
|
1 |
1 |
|
1 |
|
g |
1 |
|
|
2 |
|
g |
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Підставляючи (d) і (e) до (с) , маємо |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
P |
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|||
P r |
|
|
2 |
r2 Pr |
1 |
r2 0 |
, |
|
||||||||||||
|
|
|
|
|
||||||||||||||||
|
2 2 |
|
g |
2 |
|
|
1 1 |
|
g |
1 |
|
|
|
|
|
|||||
звідки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P r Pr |
|
|
|
|
|
||||||||
|
|
|
|
|
|
2 2 |
|
|
1 1 |
g . |
|
|
||||||||
|
|
|
|
|
|
P r2 |
Pr2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
2 |
2 |
|
|
1 1 |
|
|
|
|
|
|||
3.5.Система матеріальних точок в узагальнених параметрах a. Узагальнені координати і узагальнені швидкості та прискорення
При розв'язнні задач динаміки невільних систем з'являються деякі ускладнення. При зменшенні числа ступенів вільності, тобто при спрощенні руху системи, задача з погляду математики не спрощується, а навпаки, ускладнюється: збільшується кількість невідомих величин, що підлягають визначенню, і кількість розв'язувальних рівнянь. Крім того, навіть при ідеальних в'язях не вдалося відокремити пряму задачу динаміки від оберненої (знаходження невідомих сил – реакцій в'язей).
83

Детальний аналіз цих ускладнень привів до висновку, що для їх усунення суттєвим є вибір сукупності параметрів, які визначають положення системи у просторі.
До тепер положення точок описувалося декартовими координатами. Але існують і інші системи координат, які дозволяють для деяких видів руху системи більш просто описати положення її точок. Наприклад, при русі рідини
у круглій трубі зручно використовувати циліндричні координати. При цьому |
||||||||||||
положення частинки |
рідини |
М |
визначається |
кутом |
, |
відстанню |
r і |
|||||
координатою |
z (рис.3.9); r , |
, z - циліндричні координати точки М. Якщо |
||||||||||
покласти |
r const , |
то пряма, паралельна осі |
Oz , опише навколо осі |
Oz |
||||||||
циліндричну поверхню. |
|
|
|
|
|
|
|
|
||||
Між |
декартовими |
координатами |
(x, y, z) |
і |
циліндричними |
|||||||
(r, , z) можна знайти залежність |
|
|
|
|
|
|
|
|||||
|
|
|
|
x r cos ; |
y r sin ; |
z z . |
|
|
(а) |
|||
|
|
|
|
M(r,φ,z) |
|
|
|
|
|
M(r,у,z) |
|
|
|
|
z |
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
z |
|
|
|
θ |
z |
|
|
|
|
|
0 φ |
r |
y |
|
0 |
φ |
rsinφ |
y |
|
||
|
x |
|
M1(x,y,0) |
|
|
x |
|
M1(x,y,0) |
|
|||
|
|
|
рис.3.9 |
|
|
|
|
pиc.3.10 |
|
|
||
У |
деяких |
випадках, |
як, |
наприклад, |
при |
розповсюдженні хвиль, |
||||||
застосовують сферичні координати. Положення точки у сферичних координатах
визначається відстанню r і |
кутами |
і (рис.3.10). Між |
сферичними |
|
координатами і координатами Декарта існує залежність |
|
|||
x r sin cos ; |
y r sin sin ; |
z r cos . |
(b) |
|
Розглянемо невільну матеріальну точку, що рухається по поверхні. Рівняння поверхні (в’язі)
f (t,x, y, z) 0
Точка М має два ступені вільності N = 2. Але для вивчення руху точки М потрібно скласти три рівняння при наявності трьох невідомих величин: дві координати та модуль реакції, направленої по нормалі до поверхні.
Лагранж показав, що у випадку, коли на тіло накладено геометричні в’язі, можна вибрати систему таких недекартових координат, названих ним узагальненими координатами, котрі дозволяють розділити задачу про рух невільних точок і систем на дві окремі: спочатку визначити закон руху, потім за відомим законом руху визначити реакції в’язей.
84
Взагалі, узагальненими координатами називається система параметрів, які однозначно визначають положення всіх точок системи у кожен момент часу.
Наприклад, положення точки М можуть визначити дві незалежні
координати u, v, що називаються координатами Гауса, котрі і |
будуть |
||
узагальненими координатами. Параметричними рівняннями руху будуть |
|
||
x x(u, v, t) ; |
y y(u, v, t) ; |
z z(u, v, t) . |
(c) |
Узагальнюючи викладене, можна стверджувати, що положення системи, складеної із n матеріальних точок, яка має N ступенів вільності, визначають N
узагальнених координат q1 , q2 , , qN . Як видно, число узагальнених
координат рівне числу ступенів вільності системи.
Якщо положення точок системи визначається N узагальненими координатами, то між ними та декартовими координатами повинен існувати зв’язок. Декартові координати завжди можна однозначно виразити через узагальнені:
xi xi (t1 , q1 , q2 , , qN ),
yi yi (t1 , q1 , q2 , , qN ), (i 1,2,3, , n) (3.8)
zi zi (t1 , q1 , q2 , , qN ).
Рівняння (3.8) – параметричні рівняння в’язей, накладених на точки
системи, із параметрами qj . Дійсно, якщо система невільна, то 3n N . Виберемо N рівнянь із системи (3.8) і вирішимо відносно узагальнених
координат q j ( j 1,2, , N ) . При цьому знайдемо qj як функції декартових
координат точок системи xi, yi, zi та часу t. Підставляючи qj у інші 3n – N рівнянь системи (11.3), отримаємо k = 3n – N рівнянь, що пов’язують декартові координати xi, yi, zi та час t, тобто рівняння вигляду
fl (t, x1, y1, z1, x2 , y2 , z2 , , xn , yn , zn ) 0 |
(l 1,2, ,k), |
(3.9) |
що визначають нестаціонарні в’язі.
Введення узагальнених координат автоматично задовольняє тим умовам, що накладають в’язі на рух точок системи.
Систему трьох скалярних залежностей (3.8) можна замінити одною векторною залежністю
|
|
(t, q1 , q2 , , qN |
|
|
|
ri |
ri |
) |
(i 1,2, , n) |
(3.10) |
Час t у рівняннях (3.8) та (3.10) входить у тому випадку, коли в’язь нестаціонарна.
85
В якості прикладу розглянемо кривошипно-шатунний механізм (рис.3.11). Ведучий ланцюг – кривошип OA обертається навколо осі O , перпендикулярної до площини розташування механізму. Кривошип з’єднаний
|
|
A |
|
z |
R |
|
|
|
l |
||
|
r |
|
|
|
|
|
|
|
B |
|
|
0 |
φ |
|
|
M(x,y,z) |
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
|
y |
|
x |
рис.3.11 |
рис.3.12 |
шарнірно в точці A з шатуном |
AB і приводить його до руху. Точка |
B (повзун) рухається прямолінійно. Розташування всіх ланцюгів механізму буде відоме у кожний момент часу , якщо відомий кут повороту кривошипа .
Тому кут є узагальненою координатою для кривошипно – шатунного механізму.
Знайдемо вектор швидкості i-тої точки системи vi , виразивши його через узагальнені координати. Із кінематики відомо, що
|
|
|
V i dri . |
|
|
|
|
|
|
dt |
(d) |
|
|
|
Зауваживши, що ri - складна функція часу, отримаємо
dri
V i
dt
|
|
|
|
|
|
ri |
|
ri |
|
t |
q |
|||
|
|
|||
|
|
|
1 |
dq1 i r
dt q2
|
|
|
|
|
|
|
dq2 |
|
ri |
|
dqN |
. |
(e) |
|
qN |
|
||||
dt |
|
|
dt |
|
||
Похідні від узагальнених координат за часом називаються узагальненими швидкостями, а другі похідні за часом від узагальнених координат (або похідні за часом від узагальнених швидкостей) називаються узагальненими прискореннями. Позначаються вони відповідно
|
|
|
|
|
|
|
|
|
dqj |
q |
|
|
|
|
|
(j = 1,2,…,N). |
|||||||||
|
|
|
|
|
|
|
|
|
|
dt |
j |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
d |
2q |
j |
|
|
dq |
j |
|
|
q |
|
|
(j = 1,2,…,N). |
|||||||
|
|
|
|
|
|
dt |
2 |
|
|
dt |
|
|
|
j |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Швидкість і-тої точки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|||
V i |
ri |
|
ri |
q1 |
ri |
q2 |
|
|
ri |
|
qN |
|
ri |
|
ri |
|
q j . |
||||||||
t |
q |
q |
q |
|
|
t |
q |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
N |
|
|
j 1 |
j |
|
||||||||||
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(3.11 а)
(3.11 b)
(3.12)
86
Із (3.12) видно, що вектор швидкості – лінійна функція узагальненої швидкості.
Знайдемо співвідношення, котре буде використано при виводі рівнянь
Лагранжа другого роду – частинну похідну від швидкості vi по узагальненій
швидкості |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
V i |
|
ri |
, |
|
V i |
|
|
ri |
, |
… , |
V i |
|
ri |
, |
|
||
|
q |
q |
|
q |
|
q |
q |
N |
q |
N |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
|
1 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|||
або: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
V i |
|
ri |
, |
|
|
( j 1,2, , N ) |
(3.13) |
|||||||
|
|
|
|
q j |
q j |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б. Узагальнені сили та їх визначення
Надамо узагальненим координатам приросту
q1 q1 ; |
q2 q2 ; . . . ; |
qN qN |
Новий радіус-вектор із (11.5) буде визначено як
|
|
|
|
q1, q2 |
q2 , , qN |
qN ) (i 1, 2, , N) |
ri |
r |
i r i |
(t, q1 |
Звідси знаходимо ri як головну частину приросту функції
|
|
|
|
|
|
|
|
|
|
|
||
|
r |
|
r |
|
r |
|
N |
r |
|
|
||
ri |
|
i |
q1 |
i |
q2 |
|
i |
qN |
|
i |
|
qj . |
q |
q |
q |
|
q |
|
|||||||
|
|
|
|
N |
|
j 1 |
j |
|
||||
|
|
1 |
|
2 |
|
|
|
|
|
|||
(а)
(3.14)
Формула (3.14) показує приріст ri для випадку коли узагальнена
координата отримує приріст q1 .
До поняття про узагальнені сили прийдемо, виразивши елементарну
роботу A через узагальнені координати. Знайдемо елементарну роботу сил, що діють на точки системи, на можливих переміщеннях, вирахувавши її як скалярний добуток
|
n |
|
|
|
|
n |
|
|
|
|
||
A Ai |
|
Fi |
ri . |
|
||||||||
Підставимо значення r |
i 1 |
|
|
|
i 1 |
|
|
|
|
|||
і отримаємо |
|
|
|
|
||||||||
i |
|
n |
|
|
r |
|
|
|
|
|||
|
N |
|
|
|
|
|||||||
|
|
|
i |
|
|
|
|
|
|
j |
|
|
A |
|
|
|
F |
|
|
i |
|
q |
. |
||
|
|
|
|
|
|
q j |
|
|
|
|
||
|
j 1 i 1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
ri |
|
|
|
|
|
Вираз |
Qj |
Fi |
|
|
|
|
|
|
|
|
||
|
q |
|
|
|
|
|||||||
|
|
|
i 1 |
|
|
j |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
(b)
(3.15)
(3.16)
називається узагальненою силою. Елементарна робота набуває вигляду
87
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
A Qj qj |
Q1 q1 |
Q2 q2 QN qN (3.17) |
||||||
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
Щоб зрозуміти фізичний зміст узагальненої сили, |
||||||||
|
|
|
розглянемо елементарну роботу, |
виконану силою, що |
|||||||
|
|
|
діє на одну матеріальну точку |
|
|
|
|||||
|
|
|
|
|
A X x Y y Z z. |
(c) |
|||||
|
pис.3.13 |
Для матеріальної точки декартові координати є |
|||||||||
|
|
|
|||||||||
|
|
|
також узагальненими. |
Це |
означає, |
що |
x, y, z |
||||
|
|
|
виражають досить малі прирости узагальнених |
||||||||
|
|
|
координат, |
тобто |
|
мають |
те ж розуміння, що і |
||||
|
|
|
q1, q2 , , qn |
у |
(3.17). |
Коєфіцієнти X ,Y , Z при |
|||||
|
|
|
варіаціях узагальнених координат у виразі (3.17) є |
||||||||
|
|
|
проекціями сили. |
Тому коефіцієнти Q1,Q2 , ,QN при |
|||||||
|
|
|
варіаціях |
узагальнених |
координат |
назвали |
|||||
|
|
|
узагальненими силами |
(Qj |
можуть |
бути |
також і |
||||
|
pис.3.14 |
|
моментами сил). |
|
|
|
|
|
|
|
|
|
|
|
Узагальненою |
|
силою |
називається |
фізична |
||||
|
|
|
|
||||||||
величина, яка має таку властивость: добуток узагальненої сили та варіації відповідної їй узагальненої координати рівний елементарній роботі, що виконують сили на будь-яких
можливих переміщеннях точок системи, визначених зміною цієї узагальненої координати.
Покажемо, що для визначеного класу в’язей, які називають ідеальними, узагальнені сили залежать лише від активних сил і не залежать від реакції в’язей.
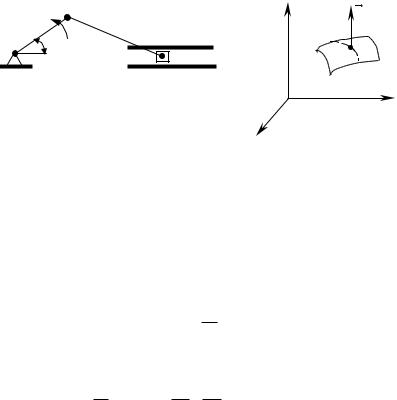
Як приклад ідеальної в’язі наведемо ідеально гладку поверхню. У зв’язку
з відсутністю сили тертя, реакція такої поверхні R направлена по нормалі до її елемента (рис.3.13). Можливі переміщення точки прикладення реакції ri
лежать в площині, дотичній до опорної поверхні. Робота реакції на можливе переміщення рівна нулю:
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
A Ri |
ri |
0 |
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
Ідеальною |
в’яззю |
можна вважати |
також жорсткий |
стрижень, що |
||||
|
|
|
|
|
|
|
|
|
|
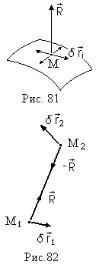
з’єднує точки М1 |
та М2 |
(рис.3.14). Реакції стрижня |
R |
та |
R направлені |
||||
вздовж нього в протилежні напрямки і рівні між собою за величиною. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
Надамо точкам М1 |
та М2 можливі переміщення |
r1 |
та |
r2 , знайдемо |
||||
|
|
|
|
|
|
|
|
|
|
роботу реакцій R |
та R |
на цих переміщеннях за формулою (3.9), що виражає |
|||||||
теорему про роботу сил, які діють на абсолютно тверде тіло. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Із рівності |
R = R |
маємо головний вектор і головний момент системи |
||||||
|
|
|
|
|
|
|
|
|
|
сил R |
та R рівні нулю, тобто |
|
|
|
|
|
|||
88

|
|
|
|
|
A R r0 |
M0 |
0 |
(3.18) |
|
Знаку нерівності тут бути не може, бо точки не можуть здійснювати рухи, при яких вони покидають в’язь.
Для ідеальних в’язей узагальнені сили залежать не від їх реакцій, а лише від активних сил. При розгляді реальних в’язей їх можна наближено вважати ідеальними, віднісши сили тертя до активних сил.
Існує інший спосіб визначення узагальненої сили.
Якщо система рухається в потенціальному силовому полі, тобто вона консервативна, то узагальнена сила виражається через силову функцію U=U(q1,q2,…,qN).Елементарну роботу консервативних сил на можливих переміщеннях можна подати у вигляді
A U U q1 U q2 |
U qN |
U |
q j |
|||||
|
|
|
|
|
N |
|
|
|
q |
q |
|
q |
j 1 |
q |
j |
|
|
1 |
2 |
|
N |
|
|
|||
Отже, для узагальненої сили дістанемо вираз
Q |
j |
U |
, |
j 1, 2, , N |
|
qj |
|
|
|
|
|
|
|
(3.19)
(3.20)
Виражаючи силову функцію через потенціальну енергію П, отримаємо
Q , j 1, 2, , N (3.21)
j |
qj |
|
Сформулюємо правило визначення узагальнених сил.
Щоб знайти узагальнену силу, потрібно надати варіацію узагальненій координаті; знайти елементарну роботу виконувану активними силами на можливих переміщеннях точок системи, що відповідають варіації узагалненої координати. Коефіцієнт при варіації узагальненої координати у виразі елементарної роботи рівен шуканій узагальненій силі.
3.6. Рівняння рівноваги системи матеріальних точок в узагальнених координатах (Рівняння Лагранжа другого роду)
Розглянемо рівняння рівноваги системи матеріальних точок в узагальнених координатах. У випадку рівноваги системи робота, виконувана на можливих переміщенняхточок системи, має бути рівна нулю
N |
|
|
|
A Qj qj Q1 q1 Q2 q2 QN qN 0 . |
(а) |
||
j 1 |
|
|
|
Рівняння (а) має виконуватись |
при довільних пиреміщеннях |
точок |
|
|
|
|
|
системи, вимірюються приростом узагальнених координат q j . Користуючись |
|||
|
|
|
|
незалежністю узагальнених координат |
q j та довільністю їх вимірювань q j , |
||
покладемо |
|
|
|
q1 0, |
q2 q3 qN 0 . |
(b) |
|
Тоді рівняння (а) матиме вид
89
A Q1 q1 0, (c)
звідки випливає, що Q1 = 0.
Аналогічно доводиться, що у випадку рівноваги системи всі узагальнені сили рівні нулю
Q2 0, , QN 0
Тобто Q j 0 , ( j 1,2,3, , N ). (3.22)
Рівності (3.19) виражають у найбільш загальному вигляді рівняння рівноваги системи матеріальних точок та абсолютно твердих тіл. Із (3.22) випливають умови рівноваги у найбільш загальному вигляді: система матеріальних точок буде знаходитись у рівновазі, якщо узагальнені сили рівні нулю.
Усі розглянуті раніше умови рівноваги є лише частковим випадком цих загальних умов рівноваги.
Повернімося до розгляду задач динаміки. Використавши принцип Деламбера, можна із рівнянь рівноваги (3.22) отримати рівняння руху. Для цього додамо до діючих на систему сил сили інерції, введучи їх у рівняння (3.22). Тоді для рухаючоїсь системи рівняння (3.22) можна записати як рівняння руху
Q j j 0 ( j 1, 2,3, , N ), (3.23)
де Фj – узагальнена сила інерції, котру на основі (3.16) можна представити так |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ri |
|
|
|
|
|
|
|
|
dV i |
|
|
|
ri |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
j |
mi W i |
|
|
|
|
|
mi |
|
|
|
. |
|
|
(e) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
dt |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
i 1 |
|
|
|
|
|
|
|
q |
j |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Перетворивши вираз (e) для узагальненої сили інерції отримаємо |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
рівняння Лагранжа другого роду: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
dV i |
|
|
r |
|
|
|
d |
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
d |
|
r |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
mi |
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
miV i |
|
|
|
|
|
|
|
|
|
miV i |
|
|
|
|
|
|
|
|
i |
|
. |
|
|
(f) |
|||||||||||||||||||
|
|
|
dt |
|
q |
|
|
dt |
|
|
q |
|
|
|
q |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
i 1 |
|
|
|
|
|
j |
|
|
i 1 |
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
i 1 |
|
|
dt |
j |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Розглянемо суми, що входять у (f). На основі (3.13) знайдем |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
r |
|
|
|
|
|
|
|
|
V i |
|
|
|
|
|
|
|
|
|
|
|
|
|
V i V i |
|
|
|
|
|
T |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
miV i |
|
|
|
i |
|
miV i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mi |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
(g) |
|||||||||||||||||||
|
q |
|
q |
|
|
q |
|
|
|
|
2 |
|
|
|
q |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
i 1 |
|
|
|
j |
|
|
i 1 |
|
|
|
|
j |
|
|
|
|
j |
|
i 1 |
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Перетворимо і другий доданок виразу (f) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
d |
|
r |
|
|
|
|
|
|
V i |
|
|
|
|
|
|
|
|
|
|
V i V i |
|
|
|
|
|
T |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
miV i |
|
|
|
|
|
|
|
i |
|
|
miV i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(h) |
|||||||||||||
dt |
|
q |
|
q |
|
|
|
|
q |
|
|
|
2 |
|
|
|
|
q |
|
|||||||||||||||||||||||||||||||||||||||||
i 1 |
|
|
|
|
|
j |
|
|
i 1 |
|
|
|
|
|
j |
|
|
|
|
|
|
j |
i 1 |
|
|
|
|
|
|
|
|
|
j |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Підставивши (g) та (h) у (e), отримаємо вираз для узагальненої сили |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
інерції |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
d |
|
T |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(i) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qj |
|
|
|
dt qj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Взявши до уваги (i), можна написати рівняння руху (3.23) у розгорнутому вигляді
90
