
denbnovetsky
.pdf
станцій. Для побудови систем супутниковому зв'язку використовують у основному три різновиду ШСЗ – на високої еліптичної орбіті (>ВЭО), геостаціонарної орбіти (ДСО) інизковисотной орбіті (НБО).
Недоліки супутниковому зв язку
Слабка перешкодозахищеність. Величезні відстані між земними станціями і супутником є причиною, що безпосереднє відношеннясигнал/шум на приймальнику дуже невелика (набагато менше, ніж більшість радіорелейних ліній зв'язку). А, щоб у умовах забезпечити прийнятну ймовірність помилки, доводиться використовувати великі антени, малошумливі елементи складні перешкодостійкі коди. Особливо гостро цю проблему стоїть у системах рухомого зв'язку, позаяк у нього є обмеження на розмір антени і, зазвичай, на потужність передавача.
Вплив атмосфери. На якість супутниковому зв'язку надають сильний вплив ефекти в тропосфері і іоносфері.
Іоносферні ефекти. Ефекти в іоносфері обумовлені флуктуаціями розподілу вільних електронів. До іоносферних ефектіввідносять мерехтіння, поглинання,затримку поширення, дисперсію, зміна частоти, обертання площини поляризації. Всі ці ефекти послаблюються зі збільшенням частоти. Для сигналів з частотами, великими 10 ГГц, їхнього впливу невелика.
Затримка поширення сигналу. Проблема затримки поширення сигналу однак зачіпає всі супутникові системи зв'язку. Найбільшою затримкою мають системи, використовують супутниковий ретранслятор на геостаціонарної орбіти. І тут затримка, обумовлена конечністю швидкості поширення радіохвиль, становить приблизно 250 мс, і з урахуванням мультиплексування, комутації і затримок обробки сигналу загальна затримка їх може становити до 400 мс.
9. Залежність пропускної здатності каналу зв’язку від відношення сигналу до шуму.
Пропускная способность по каналу с шумом равняется:
С = F 2 (1+S/N) (бит/с),
где S/N - соотношение сигнал-шум в канале, F– полоса частот канала.
В цифровых системах параметром, эквивалентным отношению S/N, является отношение Eb/N0, которое определяется как отношение количества энергии в бите информации к спектральной плотности шумов.
10. Відношення сигналу до шуму в оптимальному гаусівському каналі в залежності від питомих витрат смуги та різновиду сигналу. Оптимальна система передачі інформації та межа Шенона.
Определим показатели гауссовского канала, взяв за основу модифицированную формулу Шеннона:
C0 = Fэкв log 2 (1 c Pc ) .
Pш
Введем в рассмотрение два понятия: удельные затраты полосы (УЗП) и удельные затраты энергии (УЗЭ), т. е. затраты полосы и энергии для передачи одного бита информации:
|
F |
Fэкв , |
(1) |
|
|
|
|
||||
|
|
C0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
E0 |
|
PcT0 |
, |
(2) где |
E |
|
и T |
– энергия и время, затрачиваемые на |
E |
|
|
0 |
||||||||
|
|
N 0 |
|
N 0 |
|
|
0 |
|
|||
|
|
|
|
|
|
|
|
|
|||
передачу одного бита информации в гауссовском канале. Учитывая это обстоятельство, C0 * T0 = 1 [бит]. На основании выражений (1) и (2) перепишем формулу (*) в несколько
ином виде. Так как |
P |
= |
E0 |
|
E |
C |
|
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
T0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1= Fэкв |
log |
|
|
(1 |
|
E0 |
|
C0 |
|
) = |
|
|
log |
|
(1 |
|
E |
) = log |
|
(1 |
|
E |
) F , |
||||||||||||||||||
|
|
|
|
C |
0 |
|
|
|
|
2 |
|
|
|
|
|
c N |
0 |
|
F |
|
|
|
F |
|
2 |
|
c |
F |
|
2 |
|
c |
F |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
экв |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
21 (1 |
|
|
E |
) F , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 F |
1 |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 F |
1 |
c |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
E |
|
|
F |
(2 F |
1) . |
|
|
|
|
|
|
|
|
|
(3) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Выражение (3) устанавливает связь между УЗЭ и УЗП в гауссовском канале для различных классов сигнала. Класс сигнала определяет c . Отсюда видно, что с увеличением УЗП, УЗЭ уменьшаются.
lim |
|
|
ln 2 |
|
0.7 |
. |
|
|
|
|
|
|
|
|
|
|||
E |
|
|
|
|
|
|
|
|
|
|
|
|||||||
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
c |
|
c |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В соответствии с определениями (1) и (2) |
E |
|
Pc |
|
|
|
Pc |
. |
||||||||||
|
F |
P |
N |
0 |
* F |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
ш |
|
|
экв |
|
|||
Из выражения (3) получим необходимое отношение сигнал/шум для гауссовского канала
|
Pc |
|
1 |
1 |
|
|
|||
|
|
|
|
|
|
||||
h2 |
|
(2 F 1) . |
(4) |
||||||
P |
|
c |
|||||||
|
|
|
|
|
|
||||
|
ш |
|
|
|
|
|
|
||
Графические зависимости, определяемые формулами (3) и (4), выглядят следующим образом.

Красные стрелки указывают на зависимости, полученные для гауссовских сигналов, синие стрелки – для гармонических сигналов. Зависимость УЗЭ от УЗП для гауссовских сигналов характеризует границу Шеннона. Ниже этой границы ни одна система находиться не может.
Комментарии. Зависимости, приведенные на графиках, показывают, что:
1.Возможно неограниченное число оптимальных систем с определенными УЗП и УЗЭ и необходимым отношением сигнал/шум.
2.Для систем с малыми УЗЭ характерны большие УЗП и малые требуемые отношения сигнал/шум в канале. И наоборот, в системах с малыми УЗП требуются большие УЗЭ и большие требуемые отношения сигнал/шум.
3.Реальным системам передачи информации соответствуют на графике точки, лежащие выше границы Шеннона.
Под границей Шеннона понимается максимальная скорость передачи, для которой код имеет возможность исправить ошибки в канале с заданным отношением сигнал/шум. В настоящее время максимальное приближение к этой границе даѐт LDPC-код с примерной длиной блока в 10 миллионов бит.
Также, с другой стороны, под. границей Шеннона можно понищать минимальное отношение сигнал/шум, для котрого теоретически возможно безошибочная передача и декодирование блока с заданной скоростью. Например, для вида модуляции QPSK и скорости передачи 1 (бит/с)/символ минимальное отношение сигнал/шум составляет 0,25 дБ.
11.Об’єм сигналу, об’єм каналу, їхузгодження
Пропонується два варіантавідповіді на цепитанняна ваш вибір Вариант 1
Ємність каналу (англ. сhannelсapacity) – граничнашвидкістьпередаванняінформаціїцим каналом:
,
де q – кількістьелементарнихінформативнихповідомлень, щопередається за час Т. ЯкщосигналипередаютьсязішвидкістюSімпульсів за секунду, тобто:
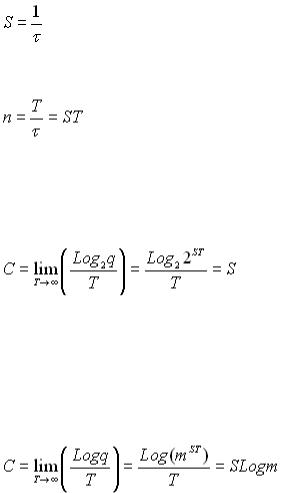
,
де τ– час передавання одного імпульсу; то за час Tможнапередати n імпульсів:
.
Для двійкового каналу, щопропускаєлишеелементарнісигнали «0» та «1», максимальна кількістькомбінаційелементарнихсигналів, яка може бути передана за час Т, складає:
 .
.
Тодіємністьбінарного каналу зв’язкувизначається:
,
тобто, чимменшою буде тривалістьімпульсу  , тимбільшою буде ємність каналу С. Для недвійкового каналу:
, тимбільшою буде ємність каналу С. Для недвійкового каналу:
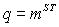 ,
,
де m – кількістьсимволів у алфавіті; і ємність каналу:
.
Ємність каналу зв’язкуСможе бути виражена у бітах на символ. Якщо до входу каналу підключенеджерелоповідомлень з ентропією на символ, щодорівнюєємності каналу зв’язку, то джерелоінформаційноузгоджене з каналом. Якщоентропіяджереламеншаніжємність каналу, то ємність каналу використовується не повністю (канал інформаційнонедовантажений).
Узгодженняджерела з каналом є досить складною справою і реалізовується за допомогоюстатистичногокодування. К. Шеннон показав, щоінформаційнеузгодження, яке досягаєтьсястатистичнимкодуванням, аналогічнеенергетичномуузгодженнювнутрішнього опору електричного генератора з навантаженням за допомогою трансформатора для передаваннявід генератора максимальноїпотужності. Тут маємо на увазіузгодженняджерела з каналом зв’язку за допомогою пристрою кодування з метою максимального використанняємності каналу.
Передача інформаціїіззавадами
Завади(англ. interference) абошуми (англ. noise) у
каналізв’язкусуттєвоускладнюютьпередаванняінформації. На приймальномубоцінемаєвпевненості, що той чиіншийелементповідомленняприйняті у тому вигляді, в якому вони булипередані. Тому під час передавання каналом іззавадамивиникаютьдвіпроблеми:
–підвищенняефективностіпередавання;
–підвищеннявірогідності (завадозахищеності) передавання.
К. Шеннон доказав, щоякщоентропіяджерелаінформації не перевищуєпропускноїздатності каналу, тобтоН ≤ С, то існує код, якийзабезпечуєпередаванняінформації каналом із
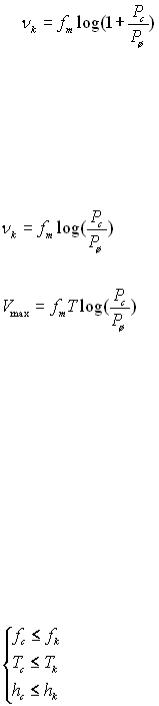
шумами з якоюзавгодно малою частотою помилокабо з якоюзавгодно малою невірогідністю. При Н > С такого коду не існує,тобтопередавання без помилокнеможливе. К. Шеннон визначивтакожмаксимальнушвидкістьпередаванняінформації:
, (2.5)
де fm – смуга частот каналу;
Pc – середняпотужність сигналу;
Рш – середняпотужністьбілого шуму.
Таким чином можнапередаватиінформацію, якщошвидкістьпередаванняінформації не перевищуємаксимальноїшвидкості каналу. Для випадку, коли середняпотужністьбілого шуму набагатобільша за середнюпотужність сигналу, тобтоPc>>Pш, у формулі (2.5) одиницеюможназнeхтувати:
.
Максимальна кількістьінформації, яка може бути передана за певний часТ:
. ( 2.6)
Оскількиця величина може бути зображена у виглядіпаралелепіпеда, то вона отрималаназвуоб’єму сигналу. Таким чином можназмінюватиокреміпараметри сигналу, не змінюючийогооб’єм. Якщо до виразу (2.6) підставитипотенційніможливості каналу передавання (час, на який канал надаєтьсякористувачу, виділенайомусмуга частот і максимальна потужність сигналу, щоможепередаватися каналом), то параметр матименазвуємність каналу. Для передавання сигналу каналом зв’язкунеобхіднощобоб’єм сигналу був не менший, ніжємність каналу, тобтонеобхідновиконатиумову:
Vc≤ V k. (2.7)
Якщо ж данаумова не виконується, то сигнал передатицим каналом зв’язкунеможливо. Може бути ситуація, приякій дана умовавиконується, але смуга частот, на яку розрахований канал, менша за смугу частот сигналу або час, якийвиділено на передаванняінформаціїменший, ніжнеобхідно, тобтоумова (2.7) розпадається на систему:
.
Одним з найбільшпоширенихспособівперетворення сигналу є варіювання величинами fc та Tc за їхнезміннимдобутком. Потужність сигналу, як правило, не збільшується.
ВАРИАНТ 2 (коротший і з використаннямінших формул)
Сигнал може бути охарактеризованийрізними параметрами. Таких параметрів, взагалікажучи, дужебагато, але для завдань, які доводиться вирішувати на практиці, істотнолишеневеликеїхнє число. Наприклад, при виборіприладу для контролю технологічногопроцесуможезнадобитисязнаннядисперсії сигналу; якщо сигнал
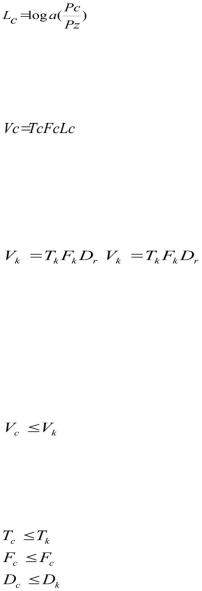
використовується для управління, істотним є йогопотужність і так далі. Розглядають три основнихпараметри сигналу, істотних для передачіінформації по каналу. Перший важливий параметр - це час передачі сигналу T с. Другою характеристикою, яку доводиться враховувати, є потужністьP з сигналу, переданого по каналу з певнимрівнемперешкодP с. Чим більшезначенняP с в порівнянніз P з,тимменшеймовірністьпомилковогоприйому. Таким чином, представляєінтересвідношенняP з / P с.Зручнокористуватися логарифмом цьоговідношення, званимперевищенням сигналу над перешкодою:
Третімважливим параметром є спектр частот F x . Ці три параметридозволяютьпредставити будь-який сигнал в тривимірномупросторі з координатами L, T, F у виглядіпаралелепіпеда з об'ємомT xF xL x . Цейтвір носить назвуоб'єму сигналу і позначається через Vx
Інформаційний канал можнахарактеризуватитакожтрьомавідповідними параметрами: часом використання каналу Т до, шириною смуги частот, щопропускаються каналом F k, і динамічнимдіапазоном каналу D kхарактеризуєйогоздатністьпередаватирізнірівні сигналу. Величина
називаєтьсяємністю каналу.
Неспотворена передача сигналівможливатільки за умови, що сигнал за своїмобсягом «вміщається» в ємність каналу.
Отже, загальнаумоваузгодження сигналу з каналом передачіінформаціївизначаєтьсяспіввідношенням
Однакспіввідношення виражає необхідна, але недостатняумоваузгодження сигналу з каналом. Достатньоюумовою є узгодження за всіма параметрами:
д12. Зв’язок довжини кодових посилок з шириною спектру сигналу – носія.
Информационная посылка длительностью Т делится на N бинарных сигналов
длительностью to = TIN с полосой f«l/to и базой v>2.
Последовательности длительностью Т являются кодовыми комбинациями, которые строят
так, чтобы выполнялось условие селекции сигналов по форме (3.
При непрерывном излучении нормированная корреляционная функция огибающей
шумоподобного сигнала, построенного на основе таких последовательностей, имеет
главный максимум, равный, единице, в области — то, то, где то — длительность сигналов
Si, и одинаковые боковые лепестки с амплитудой — 1/i/V.
, = 2т — период последовательгде т — длительность импульсов; ности.
Xi (t) — функция, описывающая одиночный импульс последовательности; Т — период
повторения импульсов; т — длительность одного импульса.
Длительность т импульсов определяется полосой пропускания каналов.
Дтс— интервал корреляции или длительность сигнала, если он рассматриваемся как
детерминированный.
Если сигнал включает ряд спектральных компонент и Дтг — интервал корреляции или
длительность t'-й компоненты, то в зависимости от значения отношения Дтк/Дтс
различают общие и селективные мультипликативные помехи (замирания сигналов).
Ширина спектра обратно пропорциональна длительности импульсов.
Псм этому для определенности сосредоточенными аддитивными помехами следует
считать те, для которых где Дсо2, Т2 — соответственно ширина спектра и длительность
помехи; Дан, Ti — ширина спектра и длительность сигнала.
Длительности прохождения сигналов и коэффициенты передачи каналов случайны.
; т—'Длительность элементарного кодового сигнала.
Общее число кодовых комбинаций длительностью Т, как обычно, N(T)=tmnK.
Дискретное сообщение представляет конечную последовательность отдельных символов
(букв); длительность этой последовательности ограничена.
13.База сигналу - переносника інформації через канал зв’язку.
База сигнала — это произведение эффективного значения длительности сигнала  и эффективного значения ширины его спектра
и эффективного значения ширины его спектра  :
:
 .
.
В простых случаях за эффективную ширину спектра можно принятьширину главного лепестка спектра. Длительность сигнала и ширина его спектра подчиняются соотношению неопределенности, гласящему, что база сигнала не может быть меньше единицы. Ограничений на максимальное значение базы сигнала не существует. То есть короткий сигнал с узким спектромсуществовать не может, а бесконечный сигнал с широким спектром — может (так называемый широкополосный сигнал, сигнал с большой базой). Примером такого рода может служить ЛЧМ-сигнал.
14.Оптимальний прийом інформації в ЕС. Критерій оптимальності.
Количественнопомехоустойчивостьопределяетсянекотороймеройсоответствияпринятогос ообщения (сигнала) переданному. Эта мера (мера качестварешения) из-за случайногохарактерапомехвсегдаявляетсястатистической и
определяетсяпотребителемсообщения (степеньючувствительностипотребителя к тем илиинымискажениям ).
Оптимальныйприемник (оптимальное правило решения) обеспечиваетнаилучшеекачестворешения, то естьобеспечиваетминимумискаженийпереданногосообщения в соответствии с меройкачества, заданнойпотребителем. Оптимальноезначениемерыкачества, котороедостигаетсяприемником в процессеоптимизации,
называется критериемоптимальностиприема (или просто критериемкачества).
При приемедискретныхсигналов в качествемерыпомехоустойчивостиобычноиспользуетсясреднийрискRср, тогдакритериемоптимальностиявляется min {Rср};
Rср = Пij P (Si , yj), (2.1)
где P (Si , yj) - совмеcтнаявероятностьпередачи S i и приема yj ;
Пij - функцияпотерь (риск потребителя) при приеме yj , когдапередавался сигнал Si ; при этом i = jсоответствует правильному приему (значения Пij =0), i ¹ j - ошибка
(значения Пij> 0) ;
m - число передаваемыхсигналов.
Приемник, работающий по этомукритерию, называетсябайесовским, а правило решения -
байесовским правилом.
Рассмотримнекоторыенаиболее часто применяемыекритерии при передаче
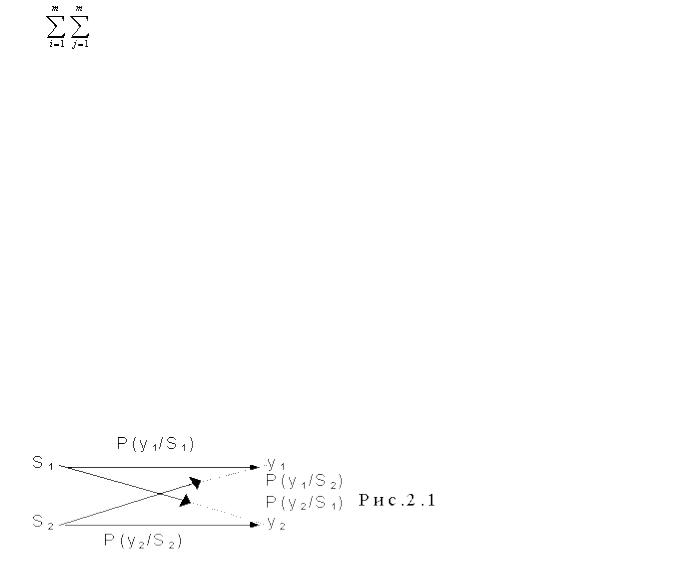
двухсигналов S1(t) и S2(t), так как в техникесвязитакая задача встречаетсянаиболее часто. При различениисигналовобязательновозникаютошибки при любоймощностисигнала и помехи, так какиз-за случайногохарактерапомехвозможнывыбросыпомехизначительнойвеличины. На рис.2.1 приведен граф переходов в системесвязи, когдапередаютсясигналы S1(t) и S2(t). Еслипередавался сигнал S1, а принят y1 - этоозначает, чтопервый сигнал принятправильно. Если же передавался сигнал S1, а принят у2- этоозначает, что при приемевместопервогосигналаполученвторой сигнал - произошлаошибка. Условныевероятности Р(у1/S1) и Р(у2/S2) естьвероятности правильного приемаэтихсигналов.
Существуетнесколькокритериевпомехоустойчивости при различениисигналов. Этикритериифактическиотличаются правилом решения, которыеопределяютположениеграницыподпространств (пунктир на рис.1.2), исходяизконкретныхтребованийпотребителя к качествуприемасигналовразличногоназначения.
1. Критерийминимальногосреднего риска.
Согласно (2.1) этоткритерий для двухсигналовминимизируетсредний риск
Rср = {П12Р(S1,y2) + П21Р(S2,y1) = П12Р(S1)Р(y2/S1) + П21Р(S2)Р(y1/S2) . (2.2)
В зависимости от значенияфункциипотерь (в данномслучаевесовыхкоэффициентов П12 и П21) этоткритерийможетприменяться в системах связиразличногоназначения с учетомтехпотерь (илиубытков), которыеявляютсяследствиемискажениясигналов S1 и S2.
Например, если сигнал S1 - отсутствиетревоги, а S2 - сигнал тревоги (пожарнаяилиохраннаясигнализация), то Р(у2/S1) - этовероятностьложнойтревоги, а Р(у1/S2) - вероятность пропуска сигналатревоги. Еслиэто система противопожарнойсигнализации, то в результате ложнойтревогиубыткисоставляют, например, 10 рублей (затраты на ложныйвыезд), а в результате пропуска тревоги (в результате чегоможетсгоретьважныйобъект) убыткисоставляютмиллионрублей. В
этомслучаевесовыекоэффициентымогутбытьсоответственноравны П12 =10, П21 = 106. Приемникдолженприниматьрешение таким образом, чтобы получить min{Rср}. Очевидно, для этойцелиграницуподпространств (рис.1.2) целесообразноудалить от
сигналатревоги S2 за счетувеличениявероятностиискажениясигнала S1, при этомуменьшитсявероятность пропуска сигналатревоги; в результате
критерий min{Rср} обеспечитминимальныеубыткисистемыпротивопожарнойбезопасности
.
2. Критерий максимального правдоподобия (критерий МП).
Критерий МП получаетсяизкритерияминимальногосреднего риска, еслипринять, что П12 = 1/P(S1), П21 = 1/P(S2).
При этомоптимальныйприемникпринимаетрешение таким образом, чтоминимизируетсязначение
l п = P(y2/S1) + P(y1/S2) . (2.3)
Критерий МП иногданазывается критериемминимумапотерьинформации, так какоптимальное правило решения в этомслучаеустанавливаетграницуподпространства (рис.1.2) так, чтобыуменьшитьвероятностьискажения того сигнала, вероятностьпередачикоторогоменьше (следовательно, этот сигнал содержитбольшеинформации).
Критерий МП применяется в системах связитакже в техслучаях, когдааприорныевероятности Р(S1) иP(S2) неизвестны.
3. Критерийидеальногонаблюдателя.
Есливесовыекоэффициенты П12 = П21 =1, то критерийминимальногосреднего риска минимизируетсреднюювероятностьошибки
pош = P(S1)P(y2/S1) + P(S2)P(y1/S2) (2.4) и
называется критериемидеальногонаблюдателя.
Критерийидеальногонаблюдателя широко применяется в системах связи, когдаискажения любого сигналаодинаковонежелательны и совпадает с критерием МП,
есливероятности Р(S1) = P(S2) = 0,5.
4. КритерийНеймана-Пирсона.
В некоторых системах передачиинформации (системах радиолокации, некоторых системах сигнализации) имеетсянеобходимостьфиксирования (задания) однойизусловныхвероятностей Р(у1/S2) или Р(у2/S1).При этомоптимальныйприемникпринимаетрешение таким образом, чтобыминимизировать ту условнуювероятность, которая не задана. Критерийоптимальности, которыйиспользуется таким приемникомназывается критериемНеймана-Пирсона.
Например, задана вероятность пропуска сигнала S1 , то есть Р(у2/S1) = a.. ТогдакритерийНеймана-
Пирсонатребуетминимизацииусловнойвероятности Р(у1/S2), обеспечиваязаданноезначени е a. Вероятность Р(у1/S2) обычнообозначается b, тогда (1-b) =
Р(у2/S2) называется качествомрешения.ПравилорешенияНейманаПирсонаобеспечивает (min b) или мах(1- b) при a = const.
Приемник при использованиикритерияНеймана-Пирсонастроится таким образом, чтобы получить достаточномалуювероятность пропуска cигнала(цели ) Р(у2/S1)=a.. С тем, что при этомможет (несмотря на минимизацию b=Р(у1/S2)) оказатьсямноголожныхтревог, приходится мириться. В этом и заключаетсясущностьданногокритерия.
15.Частотна фільтрація. Відношення сигналу до шуму на виході. За рахунок чого підвищується відношення сигналу до шуму.
Методыфильтрации: - частотная; - накопления; - корреляционный; - согласованнойфильтрации.
Частотнаяфильтрация Принцип основан на отличииспектровполезногосигнала и помех при
этомиспользуютлинейныечастотныефильтрыпозволяющие подавить помеху и улучшить с/ш.
Параметрыфильтраопределяютсяспектральными характеристиками. Частныеслучаи:
- на входприемногоустройствапоступаетузкополосный сигнал соспектральнойплотностью Sx ( ) и широкополоснаяпомеха S ( ) ;
-на входпоступаетширокополосный сигнал и узкополоснаяпомеха; - на входпоступаетпериодический сигнал и широкополоснаяпомеха
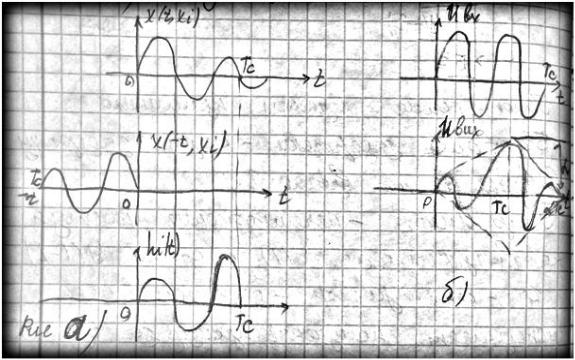
которую можна назватьобращениемсигнала, она показана на рисунке а).
