fizika / 2 / elektrodinamika

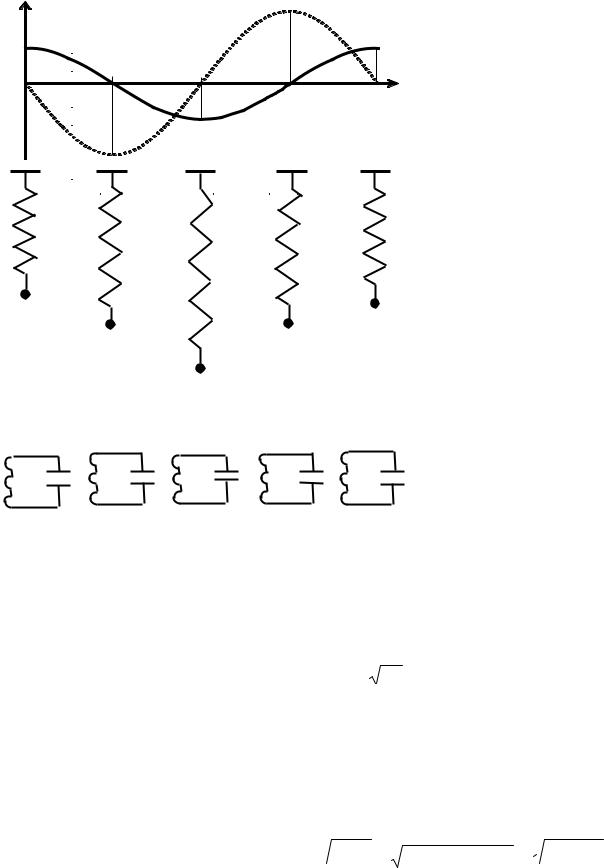
Графики зависимости смещения x и скорости υ тела, описываемые уравнениями (38.13), а также напряжения uC на конденсаторе и силы тока i в колебательном контуре, описываемые уравнениями (38.18), полагая, что α = 0, приведены на рис. 38.3 а (х и uc — сплошная линия, υ и i — пунктирная).

7. Выясним более детально характер процессов, происходящих в пружинном маятнике и колебательном контуре. Выведем тело из состояния равновесия, например, сжав пружину (рис. 38.3 б). В этом положении его смещение от положения равновесия будет максимальным (x = Xm) и на него действует макси-

мальная сила упругости, направленная к положению равновесия (см. (38.1)). Отпустим тело. Под действием этой силы оно приходит в движение. В момент времени t = (1/4)T, где T период колебания, тело проходит положение равновесия (x = 0), и скорость тела достигает максимального значения −υm (знак ми-

нус означает, что тело движется в направлении противоположном направлению оси x), а сила упругости обращается в ноль. По инерции тело продолжает двигаться. Это приводит к растяжению пружины и к появлению силы упругости, направленной противоположно направлению движения, под действием которой тело тормозится, и затем в момент времени t = (1/2)T останавливается. В этот момент скорость υ = 0 и смещение x будет максимальным ( x = Xm ). Далее те-

ло начинает двигаться в обратном направлении, и процессы повторяются. Таким образом, тело будет колебаться около положения равновесия. Колебание пружинного маятника сопровождается взаимными превращениями потенциальной и кинетической энергий маятника. При этом потенциальная энергия достигает максимального значения в те моменты времени, когда отклонение тела от положения равновесия наибольшее, а кинетическая энергия максимальная в моменты прохождения телом положения равновесия. Обратимся теперь к колебательному контуру.

Пусть в начальный момент времени (t = 0) тока в колебательном контуре нет (i = 0). В этом состоянии напряжение uc на конденсаторе будет наибольшим (uc = Ucm) (рис. 38.3 в). Под действием этого напряжения в цепи возникает электрический ток, текущий от положительно заряженной обкладки к отрицательной (имеется в виду движение положительных зарядов). Появление тока, текущего в индуктивности, приводит к возникновению э.д.с. самоиндукции es, препятствующей протеканию тока. Поэтому возрастание силы тока происходит не мгновенно. Протекание тока приводит к разрядке конденсатора и уменьшению его напряжения. В момент времени t = (1/4)T uc = 0, а сила тока i достигает максимального значения. Заряды, двигаясь по инерции, вновь заряжают конденсатор. При этом на его обкладках появляется напряжение, противодействующее протеканию тока. В результате этого сила тока уменьшается, что приводит к появлению э.д.с самоиндукции, поддерживающей ток. Поэтому убывание силы тока происходит постепенно. В момент времени t = (1/2)T, когда конденсатор полностью перезарядится, напряжение uc = Ucm и сила тока становится равной нулю. Затем процессы повторяются, и через промежуток времени, равный периоду колебаний, колебательный контур возвращается в исходное состояние. При колебаниях, происходящих в контуре, наблюдается пре-

82

r) = a + bi, где a и b действительные величины. Величину a называют действительной (вещественной) частью комплексного выражения r), bi его мнимой

r = a + bi можно изобразить в виде вектора (рис. 38.4 а), если а откладывать по оси х, а b — по оси у. Комплексную величину можно записать в тригонометрическом виде:

где r и ϕ (в радианах) модуль и аргумент комплексной величины. Связь между r,

ϕ и a, b такова: a = r cosϕ, b = r sinϕ, r = r) r)* = (a + bi)(a − bi) = a2 + b2 ,

ϕ= arctg(b/a). Здесь r)* = a − bi комплексносопряжённаявеличина.

Вматематике доказывается, что

83

где ϕ любое действительное число (рис. 38.4 б). Соотношение (38.20) называют формулой Эйлера. Используя формулу Эйлера, комплексную величину можно записать в показательном виде

комплексном виде. Воспользуемся тригонометрической и показательной запи-

Действительная часть выражения (38.21) Re(ξ) = A cos(ω0t + α) = ξ представляет собой уравнение гармонического колебания. Формально можно упростить

Комплексность амплитуды A означает, что колебание происходит с начальной фазой, отличной от нуля.

Как указывалось, умножение комплексной величины на ±i эквивалентно ум-

ножению его на e±iπ/ 2. Учитывая это, умножая правую часть уравнения (38.23) на ±i, получаем:

Это означает, что при умножении уравнения колебания на ±i, фаза колебания увеличивается или уменьшается на π/2.

Необходимо отметить, что поскольку cos ωt = Re eiωt, то можно проводить линейные математические операции — сложение, вычитание, умножение, деление,

дифференцирование и интегрирование — с eiωt. Однако возведение в степень проводить нельзя. Использование eiωt вместо cos ωt значительно упрощают мате-

84

матические расчёты, и такие комплексные функции используются в радио- и электротехнике при расчётах электрических цепей.

§39. ЭНЕРГИЯ СВОБОДНЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ

1. Рассмотрим теперь превращения энергии, происходящие в описанных ранее колебаниях. Начнём с механических колебаний. Уравнение колебаний пружинного маятника имеет вид:

где Xm и ω0 — амплитуда колебания и циклическая частота колебания (см.

(38.10)). Полная механическая энергия W пружинного маятника представляет собой сумму кинетической энергии Wk тела и потенциальной энергии Wp де-

формированной пружины, т.е.

Потенциальная энергия деформированной пружины находится по формуле Wp = kx2 /2, где k — коэффициент упругости, x — величина удлинения пружины (см. §16, т. 1), равная отклонению тела от положения равновесия. С учётом (39.1) получаем:

так как k = mω02. Кинетическая энергия тела равна Wk = (1/2)mυ2. Но, согласно (38.11), υ = −υm sin(ω0t + α), где υm = ω0 Xm амплитуда скорости тела. Учитывая это, находим, что

поскольку sin2(ω0t + α) + cos2(ω0t + α) = 1. Таким образом, как следует из

(39.5), полная механическая энергия при свободных гармонических колебаниях не зависит от времени, т.е. остается величиной постоянной. Из соотношений же (39.3) и (39.4) вытекает, что потенциальная и кинетическая энергии изменяются со временем пропорционально cos2(ω0t + α) и sin2(ω0t + α) соответственно. По-

этому, когда одна из них увеличивается, другая уменьшается. Следовательно, в процессе механических колебаний происходит периодический переход потенциальной энергии в кинетическую энергию и обратно. Важно отметить, что энергия колебаний пропорциональна квадрату амплитуды колебаний (см. (39.5)).

85

2. Рассмотрим теперь электромагнитные колебания в колебательном контуре. Уравнение колебаний заряда q на конденсаторе записывается в виде:

где qm амплитуда колебания заряда, ω0 циклическая частота колебаний

(см. (38.14)).

Энергия W колебательного контура складывается из энергии WE электрического поля конденсатора и энергии WB магнитного поля индуктивности, т.е.

тивность проводника, i сила тока, проходящего через проводник (см. (34.1)).

т.е. энергия электромагнитного поля при свободных электромагнитных гармонических колебаниях сохраняется. Из выражений же (39.8) и (39.9) следует, что со временем происходят периодические изменения энергии электрического и магнитного полей. При этом наблюдается периодический переход энергии электрического поля в энергию магнитного и наоборот, причём сумма этих энергий остаётся постоянной.

§40. СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ

В параграфе §38 были рассмотрены идеализированные незатухающие колебания, которые возникали в колебательной системе, когда не происходит потери энергии. Однако такие потери всегда есть вследствие наличия сил трения и нагревания проводников в колебательном контуре. Рассмотрим теперь реальные колебательные системы, в которых наблюдается убывание энергии, сообщённой ей.

86

1. Пружинный маятник. При движении пружинного маятника на тело, кроме силы упругости, действует сила сопротивления воздуха При небольших скоростях сила сопротивления Fc пропорциональна скорости движения υ, т.е.

Fc = −bυ, где b коэффициент сопротивления. Знак минус отражает тот факт, что сила Frc направлена противоположно υ. Если тело движется вдоль коорди-

натной оси x, то сила упругости Fупр = −kx (см. §38, п. 1) и Fc = −b dxdt , так как

υ = dxdt . Для установления характера движения тела надо составить дифферен-

циальное уравнение для этой системы на основе второго закона Ньютона:

2. Колебательный контур. Изучим теперь процессы, происходящие в реальном колебательном контуре, принимая во внимание сопротивление контура R. Составим дифференциальное уравнение, характеризующее процессы, протекающие в контуре, применив второе правило Кирхгофа uR + uc = εs. Но uR = Ri, uc = q/C и εs = −L dtdi (см. §38, п. 2). С учётом этого находим: Ri + q/C + L dtdi = 0.

3.Сопоставляя уравнения (40.1) и (40.2) видим, что у них один и тот же вид

—это однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Их можно записать в общем виде, введя некоторую

обобщенную переменную ξ вместо x и q, положив b/m = 2β и k / m = ω02 для механических колебаний и R/L = 2β и 1/(LC) = ω02 — для электрических, т.е.

87

Для решения этого уравнения надо составить характеристическое уравнение

мнимая единица. Поскольку корни характеристического уравнения комплексные, то решениемдифференциальногоуравнения(40.3) будетвыражение(см. приложение1)

где введено обозначение ω = ω02 −β2 . Здесь ω представляет собой циклическую частоту затухающих колебаний, а ω0 — собственную циклическую частоту,

в отсутствии потерь энергии при колебаниях.

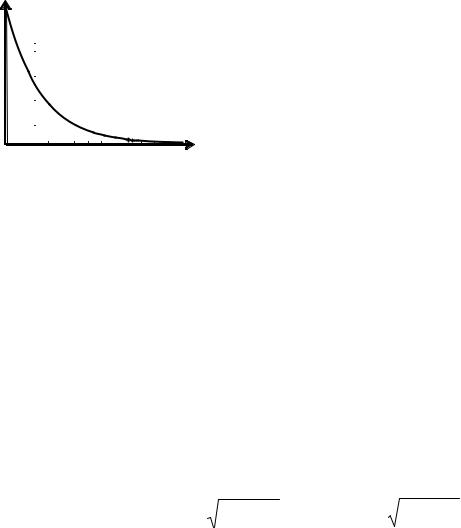
Нарисуем график зависимости (40.4) (рис. 40.1). Из графика видно, что величина ξ периодически достигает максимума и минимума. В этом смысле процессы, описываемые уравнением (40.4), можно считать колебательными. Их называют затухающими колебаниями. Наименьший промежуток времени T, через который повторяются максимумы (или минимумы) называют периодом зату-

хающих колебаний. Выражение

стоящее перед периодической функцией cos(ωt + α) в формуле (40.4), рассматривают как амплитуду затухающих колебаний. Она экспоненциально убывает со временем (см. пунктирную кривую на рис. 40.1). Величина A0 представляет

собой амплитуду колебания в момент времени t = 0, т.е. это начальная амплитуда затухающих колебаний. Величина β, от которой зависит убывание амплитуды, называется коэффициентом затухания. Чем больше коэффициент затухания, тем колебания быстрее прекращаются. Физически это означает, что в случае пружинного маятника затухание происходит быстро, если сопротивле-

88

этим трудно охарактеризовать быстроту затухания. Поэтому вводят промежуток времени τ, в течение которого амплитуда затухающих колебаний уменьшается в e раз ( e ≈ 2,718 основание натуральных логарифмов), т.е. A(t)/A(t + τ)

= e. Подставляя (40.5) в это выражение, получаем:

туд затухающих колебаний, соответствующих моментам времени, отличающимся на период колебания, т.е.

Выясним его физический смысл. Используя выражение (40.5), из (40.6), нахо-

баний за время τ. Тогда d = T/ τ = T/(NeT) = 1/Ne, т.е. логарифмический декре-

мент затухания обратно пропорционален числу колебаний, по истечении которых амплитуда затухающих колебаний уменьшается в e раз.

2) В случае, когда β2 − ω02 > 0, корни характеристического уравнения действи-

мени (с возрастанием t) ξ(t) уменьшается и при t → ∞ асимптотически приближается к нулю. Таким образом, в этом случае процесс не является колебательным. Его называют апериодическим процессом. График такого процесса для одного частного случая приведён на рис. 40.2. При механических процессах апериодические процессы возможны при движении маятника, помещённого в очень вязкую среду, и выведенного из положения равновесия. В этом случае тело медленно будет приближаться к положению равновесия, не переходя его. В случае колебательного контура апериодический разряд конденсатора возможен при большом сопротивлении контура и малой индуктивности. Действительно, если тепловые потери окажутся сравнимыми с начальной энергией конденсатора, то вся энергия при разряде превратится во внутреннюю энергию проводника, из которого изго-

89

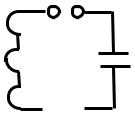
товлена индуктивность, энергия магнитного поля практически будет равна нулю и перезарядки конденсатора не произойдёт.

§41. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ЯВЛЕНИЕ РЕЗОНАНСА

Свободные колебания колебательной системы являются затухающими. Однако на практике возникает потребность в создании незатухающих колебаний, когда потери энергии в колебательной системе компенсируются за счёт внешних источников энергии. В этом случае в колебательной системе возникают вынужденные колебания. Вынужденными называют колебания, происходящие под действием периодическиизменяющегосявоздействия, асамивоздействия— вынуждающими.

1. Пружинный маятник. Рассмотрим пружинный маятник (см. §38), на который действует вынуждающая сила, изменяющаяся со временем по закону косинуса: Fв = Fm cosΩt, где Ω — циклическая частота вынуждающей силы. В данном случае тело будет двигаться под действием трёх сил: силы упругости Fупр, силы

сопротивления Fc и вынуждающей силы Fв. Предположим, что тело движется

вдоль координатной оси x. Силы, действующие на тело, также направлены вдоль этой оси. Для установления характера движения тела надо составить дифференци-

2. Колебательный контур. Составим теперь дифференциальное уравнение колебательного контура, в который включена переменная э.д.с. (рис. 41.1), изме-

няющаяся по закону e = εm cosΩt. Применяя второе правило Кирхгофа, составим дифференциальное уравнение, характеризующее процессы, протекающие в коле-

90

3. Как и в случае незатухающих и затухающих колебаний опять видим, что вид уравнений (41.1) и (41.2) одинаков и их можно записать в общем виде:

Уравнение (41.3) представляет собой неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами.

Из теории дифференциальных уравнений известно, что для нахождения общего решения неоднородного дифференциального уравнения надо найти его частное решение и сложить его с общим решением соответствующего однородного уравнения. Применительно к данному случаю запишем:

где ξодн — общее решение однородного дифференциального уравнения (40.3). Оно имеет вид

(см. формулу (40.4)).

Частное решение ξ1 находим в комплексной форме (см. §40, п. 8), воспользовавшись уравнением (41.3 а), т.е.

В этом уравнении необходимо определить амплитуду вынужденных колебаний системы и соотношение между фазой вынуждающего воздействия и фазой

возникающего вынужденного колебания. Подставляя выражение ξ)1 = A)в eiΩt и

91