
- •60. Сжимаемость грунтов. Деформативные характеристики грунтов. Испытания грунта методом одноосного сжатия. Закон компрессии.
- •61. Сопротивление грунтов сдвигу. Закон Кулона дл песчаных и глинистых грунтов. Схема испытания грунтов на сдвиг.
- •62 Фильтрационные свойства грунтов. Закон Дарси.
- •63. Напряжения в грунте от внешних нагрузок.
- •64.Метод угловых точек
- •65. Расчет оснований по 1 и 2 группе предельных состояний.
- •66. Расчет осадок методом послойного суммирования
- •67.Классификация фундаментов мелкого заложения.
- •68.Определение размеров подошвы столбчатого фундамента мелкого заложения.
- •69. Расчет плитной части фундамента на продавливания, раскалывание.
- •69 Расчет прочности плитной части на продавливание.
- •73. Основы расчета оснований свайных фундаментов по предельным состояниям.
- •74. Расчет свайных ростверков
- •72. Определение несущей способности свай-стоек и висячих свай.
- •75. Классификация фундаментов глубокого заложения
- •77 Фундаменты глубокого заложения, принципиальные методы их возведения и конструкции.
- •78. Фундаменты глубокого заложения: «Стена в грунте». Методы возведения.
- •79. Конструктивные методы улучшения работы грунтов в основаниях сооружений:грунтовые подушки, шпунтовые ограждения, создание боковых пригрузов, армирование грунтов.
62 Фильтрационные свойства грунтов. Закон Дарси.

63. Напряжения в грунте от внешних нагрузок.
Действие вертикальной сосредоточенной силы, приложенной к поверхности линейно-деформируемого полупространства.
Рассмотрим
действие вертикальной сосредоточенной
силы N,
приложенной
в точке О
к
горизонтальной плоскости, являющейся
поверхностью линейно-деформируемого
полупространства, простирающегося
в бесконечность ниже этой.
От
действия силы N
во
всех точках полупространства возникает
сложное напряженное состояние. В общем
случае в каждой точке полупространства,
несколько удаленной от точки О, в
декартовой системе координат будет
действовать шесть составляющих 

Решение этой задачи было выполнено Буссинеском (1885 г.).
Пусть
положение точки M1
определяется полярными координатами
R
и β системы координат с началом в точке
приложения силы N.
Под
действием силы N точка М1
переместится
в направлении радиуса R
на
величину s1.
Чем
дальше от точки О
будет
расположена точка M1
,тем
меньше будет ее перемещение; при R
=∞
перемещение точки М1
будет
равно нулю. Наибольшее перемещение
получит точка, расположенная на оси
z,
т. е. при β=0. С увеличением угла β
перемещения по направлению радиуса
R
уменьшаются,
и в случае 
 = 90° (на поверхности грунта) при малых
деформациях будут равны нулю.
= 90° (на поверхности грунта) при малых
деформациях будут равны нулю.


 , где
, где 

Действие нескольких сосредоточенных сил
Если
к поверхности линейно- деформируемого
полупространства приложено несколько
сил (N1,N2,…,Nn),
то при прямой пропорциональности между
напряжениями и деформациями можно
использовать принцип суперпозиции и
найти значение 
 в любой точкеM
простым суммированием:
в любой точкеM
простым суммированием:

Значения
K
определяются в зависимости от отношения



Действие любой распределенной нагрузки.
Пусть к поверхности изотропного линейно-деформируемого полупространства в пределах площади А приложено распределенное давление. Загруженную площадь можно разбить на небольшие прямоугольники со сторонами bi и li и более сложные фигуры по ее контуру. С некоторым приближением давление, распределенное в пределах i-го прямоугольника, можно заменить равнодействующей Ni, приложенной в центре тяжести этого давления.
Определим
напряжение 
 от распределения местной нагрузки.
от распределения местной нагрузки.
 где
Ki-
коэффициент зависит от отношения ri/z
где
Ki-
коэффициент зависит от отношения ri/z

Действие местного равномерно распределенного давления.
При
равномерно распределенном давлении
после интегрирования по прямоугольной
площади загружения значения 
 z
для
точек, расположенных под центром
прямоугольной площади загружения
будут
z
для
точек, расположенных под центром
прямоугольной площади загружения
будут

где а — коэффициент, принимаемый по табл из СНиП; р —равномерно распределенное давление.
При
определении напряжения 
 z
на
глубине z
под
центром площади загружения значение а
принимают
в зависимости от величин
z
на
глубине z
под
центром площади загружения значение а
принимают
в зависимости от величин 
 =l/b
и,
=l/b
и,

 =
2z/b
(где
=
2z/b
(где
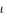
 — длинная сторона прямоугольной
площади загружения;b
—
ее ширина).
— длинная сторона прямоугольной
площади загружения;b
—
ее ширина).
Если известно угловое сжимающее
напряжение, то по нему легко определяются
и сжимающие напряжения для любой точки
полупространства, загруженного
равномерно распределенной нагрузкой,
приложенной по прямоугольной площади.
Для этого используется метод угловых
точек. При этом возможны следующие
варианты расположения точки М:
1)Точка М находится на контуре
прямоугольника, и величина σz определяется
как сумма двух угловых напряжений для
загруженных прямоугольников І и ІІ:
σz=(kІz+kІІz)*P
2) Точка М находится внутри прямоугольника,
и величина σz определяется как сумма
четырех угловых напряжений прямоугольников
І,ІІ,ІІІ и ІV:
σz=(kІc+kІІc+ kІIІc + kІVc)*P
3) Точка М расположена вне прямоугольника,
и величина определяется как сумма
угловых напряжений прямоугольников
ІІІ и ІV, взятых со знаком минус , и
угловых напряжений І и ІІ со знаком
плюс; для этого последнего случая
напряжения для всех горизонтальных
площадок по вертикали, проходящей через
точку М, будут равны:
σz=(kІc+kІІc-kІIІc-kІVc)*P
где Р- интенсивность внешней равномерно
распределенной нагрузки;
kІckІІckІIІckІVc-
угловые коэффициенты, определяемые по
таблице в зависимости от отношений
α=l/bи β=z/bдля каждого рассматриваемого
прямоугольника.
Метод угловых точек широко используется
для определения взаимного влияния
смежных фундаментов на деформацию их
оснований.
64.Метод угловых точек

