
учебник , электродинамика
.pdf
2. Колебания в системе, в которой отсутствуют потери энергии и внешнее вынуждающее воздействие, описываются дифференциальным уравнением
d 2ξ |
+ ω02ξ = 0. Решением этого уравнения является функция вида |
dt 2 |
|
ξ(t) = A cos(ω0t + α). Процессы, при которых какая-либо физическая величина изменяется со временем по закону косинуса или синуса, называются гармоническими. Колебания характеризуются амплитудой A, циклической частотой ω0, фазой колебания ω0t + α; начальной фазой колебания α. Амплитуда — это наибольшие значение колеблющейся величины. Циклическая частота равна числу колебаний за 2π секунд, Циклическая частота связана с периодом T и частотой ν колебания соотношением ω0 = 2π/T = 2πν. Период это время одного пол-
ного колебания; частота число колебаний, совершённых за одну секунду. Следовательно, в системе происходят гармонические колебания с циклической частотой ω0, называемой собственной частотой колебательной системы, кото-
рая зависит от характеристик системы. Для пружинного маятника ω0 =  k / m, где k коэффициент упругости пружины, к которой подвешено тело массой m. В случае колебательного контура ω0 =1/
k / m, где k коэффициент упругости пружины, к которой подвешено тело массой m. В случае колебательного контура ω0 =1/  LC. Здесь L и C величина индук-
LC. Здесь L и C величина индук-
тивности и ёмкости. При механических колебаниях под ξ(t) подразумевается смещение (отклонение) тела от положения равновесия, а при электромагнитных
величина заряда конденсатора в любой момент времени.
3.Колебания в системе, в которой имеются силы сопротивления, описываются
дифференциальным уравнением |
d 2ξ + 2βdξ |
+ ω02 |
ξ = 0. Решением этого уравне- |
|||
|
|
dt 2 |
dt |
|
|
|
ния при β2 < ω2 |
будет функция |
ξ(t) = A e− βtcos( |
ω2 |
−β2 t + α), которая описы- |
||
0 |
|
|
0 |
|
0 |
|
вает затухающие со временем колебания, поскольку амплитуда A0e−βt убывает по экспоненциальному закону. Величину β называют коэффициентом затухания. Частота таких колебаний ω= ω02 −β2 отличается от частоты колебаний ω0
той же системы, в которой отсутствуют силы сопротивления. Причиной затухания свободных колебаний является потеря энергии колебаний вследствие различных причин. Так, в случае механических колебаний механическая энергия превращается во внутреннюю энергию из-за наличия сил трения, а при электромагнитных колебаниях в колебательном контуре энергия уменьшается из-за превращения её во внутреннюю энергию проводника, который при прохождении по нему тока на-
гревается. В случае, когда β2 > ω02 колебаний в системе не возникает.
4. Вынужденными называются колебания, обусловленные периодическими внешними воздействиями. Если эти воздействия изменяются со временем по закону B(t) = B cosΩt, то дифференциальное уравнение, описывающее вынуж-
102
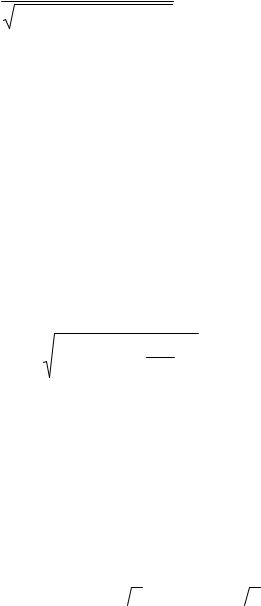
денные колебания системы, имеет вид: d 2ξ + 2βdξ |
+ ω02ξ = B cosΩt. Из реше- |
|
dt 2 |
dt |
|
ния этого дифференциального уравнения следует, что установившиеся колеба-
ния |
описываются |
уравнением: |
ξ(t) = Aв cos(Ωt + δ), |
где |
||
Aв = |
B |
|
амплитуда |
вынужденных колебаний, |
||
|
|
|||||
(ω02 − Ω2 ) 2 + 4β2 Ω2 |
|
|
|
|||
δ = arctg |
2βΩ |
начальная фаза этих колебаний. Из этого уравнения вытека- |
||||
Ω2 − ω2 |
||||||
|
|
|
|
|
||
|
0 |
|
|
|
|
|
ет, что вынужденные колебания происходят с частотой вынуждающей силы и амплитуда вынужденных колебаний зависит от частоты вынуждающего воздействия.
5.Явление резкого возрастания амплитуды вынужденных колебаний, когда частота вынуждающего воздействия близка к собственной частоте колебательной системы, называется резонансом.
6.При протекании переменного тока, сила которого изменяется по закону
i(t) = Im cos ωt (Im амплитудное значение силы тока, ω циклическая часто-
та изменения тока), через последовательно соединённые резистор R, индуктивность L и ёмкость C на этом участке цепи возникает напряжение u = Um cos(ωt + ϕ), где Um = ImZ амплитудное значение напряжения на этой
цепи, Z = |
R2 + (ωL − |
1 |
) 2 общее сопротивление цепи. Сдвиг фаз между |
|||||||||||
|
|
|
|
|
|
|
ωC |
|
|
|
|
|
|
|
силой |
тока |
1 |
|
и |
|
напряжением |
|
рассчитывается |
по |
формуле: |
||||
|
ωL − |
|
|
|
|
RL − RC |
|
|
|
|
|
|||
ϕ = arctg |
ωC |
|
= arctg |
, где R |
= ωL и R = 1/(ωC) индуктивное и |
|||||||||
|
|
|
|
|||||||||||
|
|
R |
|
|
|
|
|
R |
L |
C |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
ёмкостное сопротивление цепи.
7. Средняя мощность равна P = IU cosϕ, где I и U — действующие значения силы и напряжения переменного тока, cosϕ — коэффициент мощности, ϕ — сдвиг фаз между силой тока и напряжением. Действующие значения связаны с соответствующими амплитудными значениями силы тока и напряжения соот-
ношениями I = Im /  2 , U = Um /
2 , U = Um /  2.
2.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Что называется колебаниями? Приведите примеры колебаний.
2.Какие колебания называются гармоническими, свободными и вынужденными?
3.Дайте понятия амплитуды, периода, частоты, циклической частоты и фазы колебания.
4.Составьте дифференциальное уравнение свободных гармонических колебаний. Решите его.
5.Выведите закон сохранения энергии при гармонических колебаниях (для механических и электромагнитных колебаний).
103
6.Свободные колебания. Составьте дифференциальное уравнение таких колебаний. Решите его.
7.Что называется логарифмическим декрементом затухания? Каков физический смысл коэффициента и логарифмического декремента затухания?
8.Составьте дифференциальное уравнение вынужденных колебаний. Решите его.
9.Что называется резонансом и резонансными кривыми?
10.Каково условие квазистационарности переменного тока?
11.Рассмотрите цепь переменного тока из последовательно соединенных резистора, индуктивности и ёмкости.
12.Выведите формулу средней мощности переменного тока.
ЗАДАЧИ
6.1.Через какое время от начала движения точка, совершающая колебание по уравнению x = 8 cos πt, проходит путь от положения равновесия до максимального смещения?
6.2.Уравнение движения точки дано в виде x = cos(π/6)t. Найти моменты времени, в которые достигаются максимальная скорость и максимальное ускорение.
6.3.Напишите уравнение гармонических колебаний, если максимальное ускорение точки 50 см/с, период колебания 2 с и смещение точки от положения равновесия в начальный момент времени 25 мм.
6.4.Начальная фаза гармонического колебания равна нулю. При смещении точки от положе-
ния равновесия x1 = 2 см скорость точки υ1 = 3 см/с, а при смещении x2 = 3 см её скорость υ2 = 2 см/с. Найти амплитуду и циклическую частоту этого колебания.
6.5.Полная механическая энергия тела, совершающего гармоническое колебание, 30 мкДж;
максимальная сила, действующая на тело, 1,5 мН. Написать уравнение движения этого тела, если период колебаний 2 с и начальная фаза π/3.
6.6.К пружине подвешен груз. Максимальная кинетическая энергия колебаний 1 Дж. Амплитуда колебания 5 см. Найти жёсткость пружины.
6.7.Логарифмический декремент затухания математического маятника равен 0.2. Во сколько раз уменьшится амплитуда колебаний за одно колебание маятника?
6.8.Колебательный контур состоит из конденсатора ёмкостью 0,2 мкФ и катушки с индуктивностью 5,07 мГн. При каком логарифмическом декременте затухания напряжение на конденсаторе уменьшится в три раза за 1 мс?
6.9.Конденсатор ёмкостью 20 мкФ и резистор сопротивлением 150 Ом включены последовательно в цепь переменного тока частотой 50 Гц. Какую часть напряжения, приложенного к этой цепи, составляют напряжения на конденсаторе и резисторе?
6.10.В цепь переменного тока напряжением 220 В и частотой 50 Гц включены последовательно ёмкость С = 35,4 мкФ, резистор R = 100 Ом и индуктивность L = 0,7 Гн. Найти действующие напряжения на них.
6.11.Индуктивность L = 22,6 мГн и резистор включены последовательно в цепь переменного
тока частотой 50 Гц. Найти сопротивление резистора, если сдвиг фаз между напряжением и силой тока 60°.
ГЛАВА 7. ВОЛНЫ
Представление о волнах пронизывает нашу жизнь и всю современную технику: волны на море и сейсмические волны в земле, звуковые волны, электромагнитные волны (радиоволны, свет, рентгеновское излучение) и т.д. Выявление общих волновых закономерностей представляется очень важным, так как способ-
104

ствует пониманию волновых явлений, имеющих различную физическую приро-
ду. Волна это процесс распространения колебаний (возмущения) в простран-
стве. Проще всего уяснить сущность волнового процесса на обычном шнуре. Если дернуть вверх конец горизонтально расположенного шнура, то по нему побежит "горб" (волновой импульс). Это происходит потому, что рука тянет конец шнура вверх, а конец связан с соседними участками, которым передается сила действующая вверх. Один за другим последовательные участки шнура поднимаются вверх, что и приводит к появлению бегущего "горба". Такое движение называется бегущей волной (или волной). Таким образом, источником распространяющегося волнового импульса является возмущение, а условием существования волны наличие упругой среды, в данном случае шнура. В общем случае возмущением может быть или изменение давления в каком-либо месте упругой среды, или отклонение какого-либо элемента натянутой струны от положения равновесия, или изменение напряженности электрического (E), или индукции магнитного (B) полей в любой точке пространства. Любое колебание приводит к его распространению в пространстве, т.е. к появлению волны. Область пространст-
ва, внутри которой происходят колебания, называется волновым полем. Поверхность, отделяющую волновое поле от области, где колебаний ещё нет, на-
зывают фронтом волны. Все точки фронта волны колеблются в одинаковых фазах, поскольку колебания в них начинаются одновременно. Форма фронта волны может быть различной. Простейшими являются плоский и сферический фронты.
Линии, вдоль которых происходит распространение волны, называются лучами.
В однородных изотропных средах лучи перпендикулярны к фронту волны. Частицы среды не переносятся волной, они лишь совершают колебания около своих положений равновесия.
Обозначим любое возмещение буквой ξ. В общем случае величина возмущения зависит от времени и от координат ξ = (t, x, y, z). Независимо от фронта волны различают волны продольные и поперечные. В продольной волне колебания происходят вдоль направления распространения волны; а в поперечной перпендикулярно к направлениюраспространения. Вжидкихигазообразныхсредахвозбуждаютсялишь продольные механические волны (чередующиеся сжатие и растяжение среды). В твёрдыхтелахмогутвозникатькакпродольные, такипоперечныеволны.
§46. ВОЛНОВОЕ УРАВНЕНИЕ
При изучении волновых явлений основным исходным дифференциальным уравнением является так называемое волновое уравнение, вывод которого для некоторых случаев можно получить также с помощью закона Ньютона.
Рассмотрим колебания струны. Допустим, что однородная струна, натянутая вдоль оси x, имеет линейную плотность (массу единицы длины) ρл = dmdx , где
dm — масса элементарного участка струны длиною dx, и силу натяжения струны T. Струна, выведенная из положения равновесия, совершает поперечные ко-
105
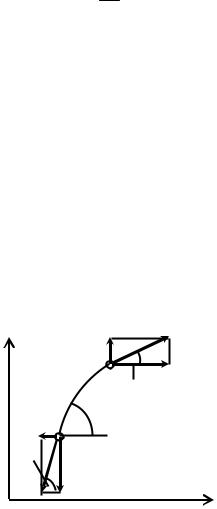
лебания. Рассмотрим вертикальное смещение dy элементарного участка струны dx массой dm (рис. 46.1). На искривлённый участок струны с одного конца действует натяжение T, направленное под углом θ к оси x, с другого также T, но под углом θ + dθ. Воспользуемся уравнением Ньютона:
dF = dm |
d 2 y |
, |
(46.1) |
||
dt |
2 |
||||
|
|
|
|||
где dF равнодействующая сила, действующая на этот участок струны в направлении колебания, т.е. вдоль оси y. На левый конец участка действует проекция силы натяжения Ty1 = −T sinθ, на правый Ty2 = T sin(θ + dθ). Тогда
проекция равнодействующей силы на ось y равна dF = Ty1+Ty2 = T sin(θ + dθ) – T sinθ. Поскольку угол отклонения струны от положения равновесия мал, то
dydx , так как производная равна тангенсу угла наклона касательной в некоторой точке к кривой. Поэтому
dF =T[(dy)x+dx − (dy)x ], |
(46.2) |
|
dx |
dx |
|
где индексы у круглых скобок указывают точки струны, для которых берутся
производные. Будем рассматривать производную |
dy |
как некоторую функцию |
|
dx |
|||
f(x). С учётом этого выражение (46.2) запишется |
|
||
|
|
||
dF = T [f(x+dx) − f(x)]. |
|
(46.3) |
Согласно правилам математического анализа, f(x+dx) – f(x) = df(x)= f′(x) dx, где
f′(x) |
производная функции f |
по x. |
|
Поскольку f(x) = |
dy |
, то f′(x) = |
d 2 y |
и |
|||||||||||||||||||||
|
dx |
dx |
2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
d 2 y |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Ty2 |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
y |
2 |
|
Tx2 |
|
f′(x) dx = dx2 |
dx. Тогда уравнение (46.3) запишет- |
|||||||||||||||||||||||
|
|
|
|
θ+dθ |
|
ся: |
dF =T |
∂ |
2 |
y |
dx. Подставляя это соотношение в |
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Tx1 |
1 θ |
|
|
∂x2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∂2 y |
|
|
∂2 y |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
(46.1), находим T |
dx = dm |
. Учитывая, что |
||||||||||||||||||||
|
θ |
|
|
|
|
|
|||||||||||||||||||||||
|
|
Ty1 |
|
x |
∂x2 |
|
∂t2 |
||||||||||||||||||||||
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
dm = ρл dx, последнее уравнение приобретает вид |
||||||||||||||||||||||||||||
|
|
|
Рис. 46.1 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
T |
∂2 y |
dx = ρ |
|
dx |
∂2 y |
или |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
∂x2 |
|
∂t 2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
‘ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
∂2 y |
= |
ρ |
‘ |
∂2 y |
. |
|
|
|
|
|
|
|
(46.4) |
|||||||
|
|
|
|
|
|
|
|
|
∂x2 |
|
|
|
∂t 2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
106
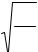
Здесь использованы частные производные, поскольку смещение y зависит как от координатырассматриваемого участкаструны, такиотвремени.
Величина T/ρл имеет размерность квадрата скорости. Действительно,
[ |
T |
]= |
Н |
|
= кг м м3 |
= ( |
м |
)2 |
. Следовательно, |
|
|
|
|
|
|
|
||
|
кг |
|
|
|
|
|
|
|
|
|
||||||||
|
ρ‘ |
|
с2 кг |
|
с |
|
|
|
|
|
|
|
|
|
||||
|
|
|
м3 |
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υ = |
|
|
|
|
|
|
(46.5) |
||
|
|
|
|
|
|
|
|
|
|
ρл |
|
|
|
|
|
|
|
|
есть некоторая скорость и уравнение (46.4) запишется: |
∂ 2 y |
= |
|
1 |
∂ 2 y |
. Заменяя |
||||||||||||
∂x |
2 |
υ2 |
∂t 2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
отклонение струны по оси y в общем случае на возмущение ξ, получаем, что
∂ 2ξ |
− |
1 |
∂ 2ξ |
= 0. |
(46.6) |
|
∂x2 |
υ2 |
∂t 2 |
||||
|
|
|
Получили волновое уравнение для струны. Оказывается, что оно справедливо для одномерных волн любой природы и, более того, его можно обобщить на случай двух- и трёхмерных волн:
|
|
|
|
|
|
∂ 2ξ |
+ |
∂ 2ξ |
+ |
∂ 2ξ |
− |
1 ∂ 2 |
ξ |
= 0. |
(46.7) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
∂x2 |
∂y2 |
∂z2 |
υ2 ∂t 2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Это уравнение принято записывать иначе: |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
Δξ − |
1 ∂ |
2ξ |
= 0, |
|
|
(46.8) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
∂ 2 |
|
∂ 2 |
|
∂ 2 |
|
|
υ2 ∂t 2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где = |
+ |
+ |
оператор Лапласа. Уравнение (46.8) является диффе- |
|||||||||||||||
∂x2 |
∂y2 |
∂z2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ренциальным уравнением в частных производных и называется волновым уравнением, которое описывает волну, распространяющуюся в произвольном направлении. Последнее уравнение было получено, как обобщение уравнения (46.6), выведенное вполне строго для колебаний струны. Однако оказалось, что волновое уравнение (46.8) носит общий характер и описывает волновые процессы не только в струне, но и в случае механических и электромагнитных волн. Более того, оно описывает и волновые свойства электронов, о чём пойдёт речь в разделе, раскрывающем некоторые аспекты квантовой механики, рассматривающей законы, управляющие миром атомов и молекул.
§47. УРАВНЕНИЕ ВОЛНЫ
107
Для описания какого-то конкретного волнового процесса в общем случае нужно решить волновое уравнение (46.7). Существуют строгие математические методы решения, которые достаточно сложны. Поэтому попытаемся найти вид решения для случая одномерных волн.
Во-первых, решение уравнения
∂2ξ |
− |
1 ∂2ξ |
= 0 |
(47.1) |
||
∂x2 |
υ2 |
∂t 2 |
||||
|
|
|
||||
должно быть функцией двух переменных x и t, которая будет описывать процесс распространения возмущения по оси x со временем t. Во-вторых, возмущением в нашем случае являются колебания (например, струны), и поэтому должна фигурировать функция вида ξ =A·cos(ωt + α), где ω, A и α — циклическая частота, амплитуда и начальная фаза колебания. В-третьих, поскольку волна есть процесс распространения колебания ξ = A·cos(ωt + α) вдоль оси x, то oно, начавшись в точке x = 0, появится через некоторое время τ в тoчке с координатой x и его можно описать уравнением ξ =A·cos[ω(t – τ) + α]. Знак минус перед τ указывает на запаздывание колебания в точке x по сравнению с началом координат x = 0. Время, в течение которого возмущение достигнет точки x, равно τ= x/υ, где υскорость распространения возмущения. Таким образом,
ξ(x, t) = A cos[ω(t − x/υ) + α]. |
(47.2) |
Очень часто значение α принимают за ноль. Тогда с учётом этого выражение (47.2) запишется, как
ξ(x, t) = A cos[ω(t − x/υ)]. |
(47.3) |
Оказывается, что полученное уравнение удовлетворяет волновому уравнению
(47.1), |
|
|
т.е. |
является |
|
|
|
его |
|
|
решением. |
Действительно, |
|||||
∂ 2ξ |
= −A |
ω2 |
cosω(t − x /υ) = −ω2 |
ξ, |
∂ 2ξ |
= −Aω2 cosω(t − x /υ) = −ω2ξ. Подстав- |
|||||||||||
∂x2 |
|
|
υ2 |
|
|
υ2 |
|
|
∂t 2 |
|
|
|
|
|
|
|
|
ляя |
в |
(47.1), Видим, |
что |
∂ 2ξ |
− |
|
1 ∂ 2ξ |
= − |
ω2 |
ξ − (− |
ω2 |
)ξ = 0, |
т.е. уравнение |
||||
∂x2 |
|
|
|
|
υ2 |
υ2 |
|||||||||||
|
|
|
|
|
|
υ2 ∂t 2 |
|
|
|
|
|
||||||
(47.3) является решением волнового уравнения (47.1). Его называют уравнением волны. Следует отметить, что теперь становится понятным смысл скорости υ, которая была введена в волновое уравнение (46.6) из соображений размерности это есть скорость распространения колебаний, т.е. скорость распространения волны (скорость распространения фронта волны). Уравнение волны (47.3) обычно записывают в ином виде. Для этого используется длина волны λ,
т.е. расстояние, проходимое волной за время, равное периоду колебания, т.е.
λ = υT |
(47.4) |
и волновое число |
|
k = 2π /λ, |
(47.5) |
108
показывающее сколько длин волн укладывается на отрезке длиной 2π метров.
Поскольку T = 1/ν, где ν частота колебаний, то из (47.4) следует, что
|
|
|
|
λ = υ/ν. |
|
(47.6) |
|
Преобразуем |
|
аргумент |
косинуса |
выражения |
(47.3). |
||
ω(t − x/υ) = ωt − |
2πx |
= ωt − |
2πx |
= ωt − kx, так как ω = 2π/T, υT = λ и 2π /λ = k |
|||
υT |
λ |
||||||
|
|
|
|
|
|||
(см. (38.8), (47.4) и (47.5)). Тогда уравнение (47.3) запишется:
109
ξ(x, t) = A cos(ωt − kx). |
(47.7) |
В выражении (47.7) A и ω амплитуда и циклическая частота волны, равная амплитуде и циклической частоте колебаний, происходящих в разных точках волны; ωt − kx фаза волны.
Уравнение волны (47.7) можно записать ещё в одном виде, зная, что ω = 2π/T
и k = 2π /λ:
ξ(t) = A cos2π( |
t |
− |
x |
). |
(47.8) |
|
|
||||
T |
|
λ |
|
||
Уравнения (47.3), (47.7), (47.8) описывают волну, распространяющуюся в положительном направлении оси x. Если волна распространяется в обратном направлении (т.е. вдоль оси −x), то очевидно уравнения волны приобретают вид:
ξ(x, t)=A cos[ω(t + x/υ)], |
(47.9) |
||||
ξ(x, t) = A cos(ωt + kx), |
(47.10) |
||||
ξ(t) = A cos2π( |
t |
+ |
x |
). |
(47.11) |
|
|
||||
T |
|
λ |
|
||
Подводя итог обсуждения уравнения волны, можно отметить следующее. Как видно из выражения (47.8), уравнение волны является периодической функцией, как относительно времени, так и координат. Действительно, в моменты времени t + nT (n = 0, 1, 2, ...) функция принимает одинаковые значения в фиксированной точке с координатой x, а в точках с координатами x + nλ она одинакова для фиксированного момента времени t. Иначе говоря, если зафиксировать точку пространства x = const (для простоты положим x = 0), то получим уравнение колебания ξ(0, t) = A·cosωt, т.е. в данной точке будет совершаться колебание с циклической частотой ω. Если зафиксировать момент времени t = const, то ξ(x) = A cos(kx + const), т.e. получим периодическое распределение отклонений частиц от положения равновесия в случае механических волн (моментальная фотография волны). Итак, была рассмотрена плоская монохроматическая волна. Её плоскостность определяется тем, что возмущение зависит только от x и не зависит от y и z (плоскость). Монохроматичность означает, что все колебания совершаются только с одной частотой.
В заключение отметим, что уравнения волн, как и уравнения колебаний, удобно записывать в комплексном виде (см. §38, п.8). Выпишем эти уравнения в тригонометрическом и комплексном виде:
ξ(x, t) = A cos(ωt − kx), ξ(x, t) = A ei(ωt-kx) .
§48. СЛОЖЕНИЕ ПАДАЮЩЕЙ И ОТРАЖЁННОЙ ВОЛНЫ
Когда бегущая волна падает на преграду, она отражается и образуется отражённая волна, которая налагается на бегущую волну. Рассмотрим получаю-
109
щуюся при этом картину на примере натянутой вдоль оси x струны длиной l, закреплённой с двух концов. Запишем уравнения падающей и отражённой вол-
ны в виде уравнений (47.7) и (47.10): ξ1 = A1cos(ωt − kx), ξ2 = A2cos(ωt + kx). В
результате сложения этих двух волн смещение ξ в любой точке струны будет определяться соотношением:
ξ = ξ1 + ξ2 = A1cos(ωt − kx)+A2cos(ωt + kx). |
(48.1) |
|||
Учтём, что на концах струна закреплена. Математически это запишется: |
||||
ξ = 0 при x = 0, |
(48.2) |
ξ = 0 |
при x = l. |
(48.3) |
Уравнение (48.1) для x = 0 в |
соответствии с |
условием |
(48.2) имеет вид |
|
0 = (A1 + A2)cosωt. Откуда ясно, что A2 = – A1. Физический смысл полученного соотношения амплитуд заключается в том, что отражённая волна изменяет фазу на π, т.е. становится равной ωt + kx + π. Учитывая изменение фазы волны, равенство амплитуд падающей и отражённой волн и отбрасывая индексы, уравнение (48.1) запишем как
|
ξ = A[cos(ωt − kx) − cos(ωt + kx)] = 2A·sinkx·sinωt, |
(48.4) |
|||
воспользовавшись |
тригонометрическим |
соотношением |
cosα − cosβ = |
||
= 2Asin |
β − αsin |
β + α. |
По сути дела полученное уравнение описывает колеба- |
||
|
2 |
2 |
|
|
|
ние с амплитудой 2A·sinkx, зависящей от координаты x, т.е. в данном случае волны нет. Воспользуемся условием (48.3) и подставим его в уравнение (48.4) 0 = 2A·sinkl·sinωt. Это условие выполняется для любого момента времени, если kl = (2π /λ)l = nπ, где n = 1, 2, ... . Откуда
λ = 2l/n. |
(48.5) |
Получили значения длин волн, которые могут существовать в струне длиной l:
λ = 2l, λ = l, λ = (2/3)l... при n = 1, 2, 3, ... соответственно. Из (48.5) следует, что n = l /(λ /2), т.е. в струне возбуждаются лишь такие волны, половина длины которых укладывается на длине струны целое число раз.
Используя уравнение (48.4) и полученные длины волн, можно рассчитать форму волны. Общая картина колебаний приведена на рис. 48.1, на котором показана так называемая стоячая волна. Стоячая волна характеризуется узлами и пучностями. Точки струны, которые всегда остаются неподвижными (например, точки У1 и У2 рис. 48.1 в) называются узлами. Их координаты можно определить из уравнения(48.4), полагая ξ = 0, что приводит к соотношению sinkx = sin(2π/λ)x = 0. Это равносильно требованию (2π / λ)x = n, где n = 1, 2, 3, ... . Отсюда координаты узлов
x = (λ /2)n . |
(48.6) |
Пучности — это точки струны, колеблющиеся с максимальной амплитудой, т.е. 2A (например, точки П1, П2, П3 рис. 48.1 в). Из уравнения (48.4) получаем
2A = 2A·sinkx. Отсюда sinkx = 1 и (2π /λ)x = (2n+1)π /2 при n = 1, 2, 3, ... . Откуда получаем уравнение для координат пучностей
110
