
учебник , электродинамика
.pdf
§25. ЗАКОН БИО – САВАРА – ЛАПЛАСА И ЕГО ПРИМЕНЕНИЯ
1. Для современной физики и особенно электронной техники очень важно уметь рассчитывать индукцию магнитного поля, создаваемого каким-либо уст-
r |
|
|
ройством, по которому протекает электриче- |
||||||||||
dB |
|
|
ский ток. В целом это и составляет одну из ос- |
||||||||||
|
|
|
|||||||||||
|
|
|
новных задач учения о магнетизме. Существует |
||||||||||
|
D несколько подходов к решению этого вопроса. |
||||||||||||
|
|
|
Рассмотрим методы расчёта магнитных полей, |
||||||||||
|
|
|
основывающиеся на законе Био – Савара – Лап- |
||||||||||
r |
|
|
ласа, который сначала и сформулируем. |
|
|||||||||
I |
|
|
|
Лаплас, анализируя опыты Био и Савара по изу- |
|||||||||
r α |
|
|
чению магнитных полей постоянных токов раз- |
||||||||||
dl |
|
|
личной формы, показал, что элементарная индук- |
||||||||||
|
|
|
|||||||||||
|
|
|
ция dB магнитного поля в некоторой точке D, соз- |
||||||||||
|
|
|
даваемая элементарным участком dl, по которому |
||||||||||
Рис. 25.1 |
|
|
течёттоксилойI (рис. 25.1) находитсяпоформуле: |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
μ |
0 |
μ |
|
I [dl rr] |
|
|
|
|
|
|
|
dB = |
|
|
|
|
. |
|
|
(25.1) |
||
|
4π |
r3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь dlr— вектор, по модулю равный длине dl элемента проводника и совпа- |
|||||||||||||
дающий с направлением тока, rr |
— радиус-вектор, проведённый из элемента dl |
||||||||||||
проводника в точку, в которой вычисляется поле, r — модуль вектора rr |
, [dl rr] |
||||||||||||
— векторное произведение указанных векторов, μ магнитная проницаемость среды, μ0 = 4π10–7 Гн/м — магнитная постоянная, где Гн (генри) — единица ин-
дуктивности проводника (см. §32). Соотношение (25.1) носит название закона
Био – Савара – Лапласа.
Согласно правилу векторного произведения векторов, dB перпендикулярно к
плоскости, проведённой через векторы dl и r , т.е. и к r . Направление линии магнитной индукции, проходящей через точку D, можно найти и по правилу правого винта (см. §23, п. 3): если поступательное движение винта совпадает с направлением тока, то его вращательное движение даёт направление линии магнитной
индукции(см. рис. 25.1). Вектор dB направленпокасательнойкэтойлинии.
Из (25.1) следует, что модуль вектора dB равен: |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dB = |
μ0μ |
|
I dl sinα |
, |
|
(25.2) |
|
4π |
r2 |
||||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
где α — угол между векторами dl |
и r. |
|
|
|
|||||
Используя выражение (25.1), рассчитывают индукцию B магнитного поля, создаваемого проводником длиною l, по которому течёт ток силой I, в любой точке (например, в точке D):
53
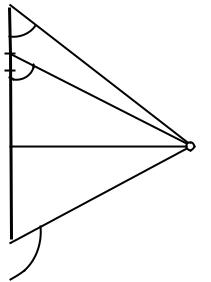
r |
μ |
0 |
μ |
|
I [dl |
rr] |
|
|
|
B = ∫ |
|
|
|
|
|
|
. |
(25.3) |
|
4π |
r3 |
|
|
||||||
l |
|
|
|
|
|
||||
Расчёт индукции магнитного поля по этой формуле в общем случае сложен. Однако в ряде практически важных случаев оказывается сравнительно простым. Например, длямагнитногополя, создаваемогопрямымбесконечнымпроводомстоком.
2. Магнитное поле прямого тока. Пусть по прямолинейному проводнику
течёт постоянный ток силой I. Найдём индукцию B магнитного поля в произвольной точке D, отстоящей от проводника на расстоянии a (рисr. 25.2). Мыс-
ленно выделим на проводнике элементарный участок dl. Вектор dB , созданный этим элементом проводникаr с током, направлен перпендикулярно к плоскости
чертежа от нас. Векторы dB от всех элементов тока имеют одинаковое направление (воспользуйтесьr правилом правого винта). Поэтому векторное сложение
векторов dB заменяем сложением их модулей. Тогда с учётом (25.2) получаем
B = ∫dB = ∫ |
μ0μ |
|
I dl sinα |
. |
(25.4) |
|
|
|
|||||
l |
l |
4π |
|
r 2 |
|
|
В качестве переменной интегрирования удобно выбрать угол α, выразив через него все остальные переменные. Обозначим расстояние от элементарного участка до точки O через l, которое меняется в зависимости от положения этого участка. Из прямоугольного треугольника OCD имеем:
r = a/sin α, |
(25.5) |
l = a ctg α. |
(25.6) |
Из выражения (25.6) находим дифференциал l, который по абсолютной величине можно рассматривать как длину dl элемента тока
dl = a |
|
− |
1 |
|
dα = |
a |
|
dα.. |
(25.7) |
α1 |
|
|
|
||||||||
|
|
|
C |
|||||||
sin 2α |
sin 2 |
|
||||||||
|
|
|
|
|
α |
dl |
α |
|||
Подставляя соотношения (25.5) и (25.7) в выражение (25.4) и учитывая, что α изменяется от α1 до
α2, |
|
|
находим, |
что |
B = |
μ |
μ α2 |
|
|
|||
|
|
0 |
∫sin α dα = |
|||||||||
|
|
|
|
|
|
|
|
|
4πa α |
|
|
|
|
|
|
I |
|
|
|
|
|
|
1 |
|
|
= μ |
|
μ |
(cosα − cosα |
|
). |
Для бесконечно длин- |
||||||
|
4πa |
|
||||||||||
|
0 |
|
1 |
|
2 |
|
|
|
|
|
|
|
ного проводника α1 = 0 и α2 = π. Поэтому |
|
|
||||||||||
|
|
|
|
|
|
|
|
B = μ0μ |
I |
. |
||
|
|
|
|
|
|
|
|
2πa |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
l
0
 I
I
 α2
α2
r
a |
D |
|
dB |
||
|
Рис. 25.2
(25.8)
54

|
Из этой формулы следует, что модуль B индукции |
|
B |
магнитного поля одинаков во всех точках окружности |
|
3 |
радиусом a и убывает с увеличением расстояния от |
|
I |
проводника с током. Картина линий магнитной ин- |
|
дукции показана на рис. 25.3. |
||
|
||
|
3. Магнитное поле на оси кругового тока. Другим |
rважным случаем является расчёт магнитного поля кру-
r |
B2 |
гового тока. Мысленно выделим на проводнике эле- |
B1 |
|
ментарный участок длиной dl. Согласно закону Био − |
Рис. 25.3 |
|
Савара − Лапласа, этот элемент тока создаёт элемен- |
тарную индукцию dB магнитного поля, перпендикулярную к радиус-вектору r (рис. 25.4). Разложим вектор dB на две составляющие dB1 , параллельную оси кругового тока, и dB2 , перпендикулярную к ней. Тогда dB = dBr1 + dBr2 . Индук-
ция B магнитного поля в точке D равна векторной сумме dB в той же точке, т.е. |
||||
Br |
= ∫dBr |
=∫(dBr1 + dBr2 ) = ∫dBr1 + ∫dB2 , поскольку суммирование бесконечно малых |
||
|
l |
l |
l |
l |
величин — это интегрированиеr . Здесь интегрирование проводится по окружности длиною l. Составляющие dB2 от различных элементарных участков dl с током имеютrвсевозможныеr направленияr . Поэтому их векторная сумма равна нулю, т.е. ∫dB2 = 0 . Тогда B = ∫dB1 . Поскольку векторы dB1 от всех элементов тока имеют
l |
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
одинаковое направление, то их векторное |
dl |
|
|
|
|
|||||||||||
сложение заменим сложением их модулей |
|
|
dB2 |
dB |
||||||||||||
B = ∫dB1 . |
Из рис. 25.4 видно, |
что dB1 |
|
β |
|
|
|
|||||||||
|
l |
|
|
|
|
|
|
|
|
|
|
|
r |
|
||
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|||
= dB·cos β. |
Из закона Био − Савара − Лапла- |
|
|
|
||||||||||||
|
|
|
β |
|||||||||||||
са (см. (25.2)) dB = |
μ0μ |
|
I dl |
, так как угол |
|
|
|
|
||||||||
0 |
|
a |
|
|
||||||||||||
4π |
r2 |
I |
D |
dB |
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
между |
векторами |
dl |
и rr |
равен 90° и |
|
|
|
1 |
||||||||
|
|
|
|
|
||||||||||||
sin α = 1. |
|
Учитывая |
|
это, |
запишем |
|
|
|
|
|
||||||
B = |
∫ |
dBr = |
∫ |
dB cos β= |
∫ |
μ0μ |
I dl cosβ. |
|
|
Рис. 25.4 |
|
|||||
|
|
1 |
|
|
4π |
r 2 |
|
|
|
|
|
|
||||
|
l |
|
|
l |
|
|
l |
|
|
|
|
|
|
|||
Для данной точки D величины cos β и r являются постоянными. Вынося из под ин-
теграла все постоянные, получаем, что B = |
μ0μ I cosβ |
∫dl. Но ∫dl = 2πR, посколь- |
|
|
4π r 2 |
l |
l |
ку суммирование элементарных дуг окружностей даёт длину окружности. Итак,
B = μ0μIR cos β . 2r2
Изрис. 25.4 видно, чтоcos β = R/r и r =  a2 + R2 . Сучётомэтогонаходим
a2 + R2 . Сучётомэтогонаходим
55

B = μ0μ |
|
IR2 |
. |
(25.9) |
|
2(a2 |
+ R2 )3 / 2 |
||||
|
|
|
Из формулы (25.9) следует, что индукция магнитного поля в центре кругового тока (a = 0) равна
B = μ0μ |
I |
. |
(25.10) |
|
|||
|
2R |
|
|
§26. ВЗАИМОДЕЙСТВИЕ ПАРАЛЛЕЛЬНЫХ ТОКОВ
1. Рассмотрим два бесконечно длинных проводника, расположенных параллельно друг другу, по которым течёт постоянный ток силой I1 и I2, в противо-
положных направлениях (рис. 26.1, на котором показано поперечное сечение проводников плоскостью чертежа, ток I1 течёт от нас, а I2 — на нас). Расстоя-
ние между проводниками равно a. Каждый |
|
|
|
из проводников создаёт вокруг себя магнит- |
dF |
I1 |
I2 • |
ное поле, которое действует на ток, текущий |
|
dF2 |
|
по другому проводнику. Поэтому между ни- |
1 |
a |
|
|
|
||
ми возникают силы взаимодействия. В дан- |
|
|
|
ном случае силы отталкивания. Если токи |
|
Рис. 26.1 |
|
текут в одном направлении, то между про- |
|
|
|
|
|
|
водниками возникают силы притяжения. Эти силы равны по модулю и на единицу длины проводника действует сила, находимая по формуле:
dF1 |
= |
dF2 |
= dF |
= |
μ0μ |
|
I1I2 |
. |
(26.1) |
dl |
dl |
2π |
|
||||||
|
dl |
|
|
a |
|
||||
2. Пусть два параллельных проводника с током находятся в вакууме (μ = 1). Тогда сила взаимодействия на единицу длины проводника, согласно (26.1), равна
dFυ |
= |
μ0 |
|
I1I2 |
. |
(26.2) |
|
|
|||||
dl |
2π |
|
a |
|
||
Это выражение используется для определения единицы силы тока — ампер. Пусть силы токов, текущих по проводам, одинаковы. Тогда из (26.2), учитывая
значение магнитной постоянной (μ0 = 4π 10−7 Гн/м), следует, что если
dFυ /dl = 2 10−7 Н/м и a = 1 м, то I = 1 A, т.е. 1 А — это сила такого тока, при протекании которого по бесконечно длинным параллельным проводникам, на-
ходящимся в вакууме на расстоянии одного метра друг от друга, на отрезок проводника длиной 1 м действует сила 2 10−7 Н. Ампер является основной еди-
ницей силы тока в системе единиц СИ. Используя это, вводят единицу заряда
1 Кл = 1 А 1 с, т.е. 1 Кл — это заряд, протекающий в 1 с при силе тока в 1 А.
56

§27. ЗАКОН ПОЛНОГО ТОКА
В ряде случаев для вычисления индукции магнитного поля, создаваемого электрическим током, проще использовать так называемый закон полного тока, а не закон Био – Савара – Лапласа. Закон полного тока носит несколько абстрактный математический характер, и непосредственная физическая наглядность в нём отсутствует, что, вообще говоря, достаточно характерно для современной теоретической физики. Прежде, чем перейти к рассмотрению этого закона, введём понятие циркуляции индукции магнитного поля.
1. В §8 было введено понятие циркуляции напряжённости электрического поля и показано, что циркуляция напряжённости электростатического поля
вдоль произвольного замкнутого контура l равна нулю, т.е. ∫E dl =∫El dl = 0,
l l
что свидетельствует о потенциальности электростатического поля. Аналогичная величина вводится и при рассмотрении магнитного поля. Циркуляцией ин-
дукции магнитного поля называют интеграл
∫B dl =∫Bl dl, |
(27.1) |
|
l |
l |
|
где dlr — элементарный вектор длины контура, направленный в сторону обхо- |
||
да контура, Bl = B·cosα — проекция вектора B на направление dlr, α — угол |
||
между векторами B и dlr. |
|
|
2. Найдём циркуляцию индукции магнитного поля по окружности произвольного радиуса a, совпадающей с линией магнитной индукции. Поле создаётся током силой I, текущим по бесконечно длинному проводнику, расположенным перпендикулярно к плоскости чертежа (рис. 27.1, на котором приведено поперечное сечение проводника плоскостью чертежа и линия магнитной ин-
дукции изображена пунктиром). Индукция магнитного поля B направлена по
касательной к линии магнитной индукции. |
Преобразуем выражение |
B dl = B dl cosα = B dl , так как α = 0 и cos α = |
1. Поскольку B = μ0μI/(2πa) |
(см. (25.8)), то Br dlr = μ20πμaI dl. Циркуляцию вектора B по данному контуру, нахо-
дим |
по |
формуле |
(27.1): |
a dl |
B |
|
|
I |
I1 |
I2 |
• |
|
|
||
|
|
• I3 |
|
Рис. 27.1 |
|
Рис. 27.2 |
|
57

r |
r |
|
μ |
0 |
μI |
|
μ |
0 |
μI |
∫dl = |
μ |
μI |
|
μ |
0 |
μI |
2πa = μ0μΙ, так как |
∫dl = l = 2πa |
∫B dl |
=∫ |
|
|
dl = |
|
|
0 |
|
l = |
|
|
|||||||
|
|
|
|
|
2πa |
|||||||||||||
l |
|
l |
2πa |
|
2πa |
l |
2πa |
|
|
l |
||||||||
— длина окружности. Итак, |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
∫B dl = μ0μI. |
(27.2) |
||||||
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
Можно показать, что соотношение (27.2) справедливо для контура произвольной формы, охватывающего проводник с током. Если магнитное поле создано систе-
мой токов I1, I2, ... , In, то индукция B этого поля в соответствии с принципом суперпозиции полей равна векторной сумме индукций магнитных полей, созда-
ваемых отдельными токами, т.е. B = B1 + B2 +...+ Bn . С учётом этого для цирку- |
|||||||||
ляции B имеем ∫Br |
dlr |
=∫(Br1 + B2 +... + Bn )dl = |
∫B1 dl + ∫B2 dlr |
+ ... +∫Bn dl . |
|||||
|
|
l r |
r |
l |
l |
l |
l |
||
Согласно (27.2), ∫Bk dl |
= μ0μIk , где k — принимает значения от 1 до n. Поэтому |
||||||||
|
l |
|
|
|
|
|
|
|
|
|
|
r |
r |
|
|
n |
|
|
|
|
|
∫B dl |
= μ0μI0 + μ0μI2 +... + μ0μIn = μ0μ ∑Ik . |
|
|
(27.3) |
|||
|
|
l |
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Необходимо отметить, что в выражении (27.3) суммирование сил токов алгебраическое. Знак силы тока зависит от направления обхода и определяется пра-
вилом правого винта: если направление тока совпадает с поступательным движением винта, вращающегося по направлению обхода контура, то он по-
ложительный; ток противоположного направления считают отрицательным. Например, для системы токов, приведённых на рис. 27.2, на котором показано
n
их сечение плоскостью чертежа, ∑Ik = I1 – I2 – I3. Соотношение (27.3) и явля-
k =1
ется законом полного тока: циркуляция индукции магнитного поля по произ-
вольному замкнутому контуру равна произведению магнитной постоянной, магнитной проницаемости на алгебраическую сумму сил токов, охватываемых этим контуром.
Силу тока можно найти, используя плотность тока j (см. (15.6)): I = ∫ j dS,
S
где S — площадь поперечного сечения проводника. Тогда закон полного тока записывается в виде
|
|
|
|
|
|
∫ B dl = μ0μ∫ j dS. |
|
(27.4) |
|
|
l |
S |
|
|
|
|
|
|
|
Подводя итог, отметимr , что на основании рассмотрения циркуляции напряжённости (индукцииr r ) G какого-то поля в физике определяют два типа полей:
1. Если ∫G dl = 0, то поле называют потенциальным. Таковыми являются элек-
l
тростатическиеигравитационныеполя.
58
2. Если ∫Gr dlr ≠ 0, то поле называется вихревым. К нему относится, в пер-
l
вую очередь, постоянное магнитное поле, и, как будет показано, переменное электрическое поле.
§28. МАГНИТНОЕ ПОЛЕ БЕСКОНЕЧНО ДЛИННОГО СОЛЕНОИДА
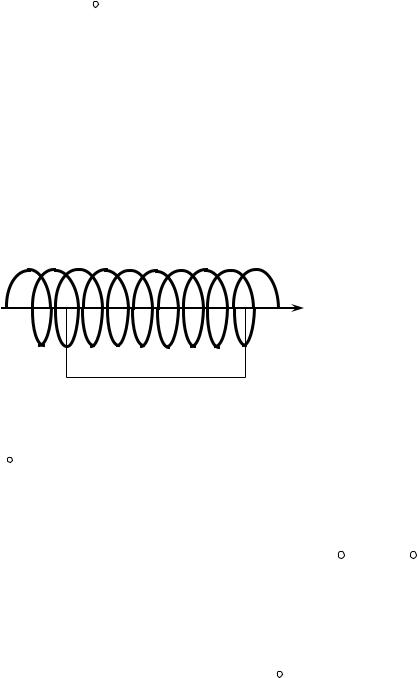
В качестве примера применения закона полного тока рассчитаем магнитное поле бесконечно длинного соленоида, по которому течёт электрический ток (рис. 28.1). (Бесконечно длинным можно считать соленоид, диаметр которого много меньше его длины). Опытным путём установлено, что магнитное поле
внутри бесконечно длинного соленоида однородное ( B = const), а вне него оно
|
|
|
|
|
|
настолько слабо, что им можно пренеб- |
|||
|
а |
|
|
б |
речь. Внутри соленоида поле направле- |
||||
|
|
|
но вдоль его оси. Для нахождения мо- |
||||||
|
|
|
|
|
B |
дуля вектора B воспользуемся законом |
|||
|
|
|
|
|
|
полного тока. Мысленно проведём |
|||
г |
|
|
|
|
в |
замкнутый контур в виде прямоуголь- |
|||
|
|
|
|
ника абвга. Тогда интеграл по замкну- |
|||||
|
|
Рис. 28.1 |
|
|
|||||
|
|
|
|
тому контуру можно представить как |
|||||
сумму |
интегралов |
по |
отдельным |
сторонам |
этого |
прямоугольника, |
т.е. |
||
∫Br dlr |
= ∫Br |
dlr + ∫B dlr |
+ ∫Br |
dl + ∫B dl . Интегралы по бв и га равны нулю, |
|||||
l |
аб |
бв |
|
вг |
га |
|
|
|
|
поскольку внутри соленоида B перпендикулярно к dl и B dlr = B·dl·cos 90°= 0. |
|||||||||
Интеграл по вг также равен нулю, так как B = 0. На участке аб направления B и |
|||||||||
dlr совпадают и Br |
dlr= B·dl. Поэтому ∫B dl = ∫B dl = B ∫dl = Bl0 , где l0 |
— |
|||||||
|
|
|
|
|
|
l |
l |
аб |
|
длина отрезка аб. Величина B вынесена за знак интеграла, так как B = const (поле однородное), а суммирование элементарных участков на отрезке аб даёт длину этого участка. Итак,
∫B dl = Bl0 . |
(28.1) |
l |
|
Пусть число витков на единицу длины соленоида равно n. Тогда общее число витков N на отрезке соленоида длиной l0 равно N = nl0, а число токов, охваты-
ваемых контуром,
N
∑Ii = NI = nl0 I. (28.2)
i=1
Подставляя (28.1) и (28.2), в закон полного тока (27.3), получаем Bl0 = μ0μnl0I. Отсюда
B = μ0μ nI. |
(28.3) |
59
Из формулы (28.3) следует, что для создания магнитного поля в соленоиде с большей индукцией поля необходимо увеличивать число витков на единицу длины (плотность намотки) и силу тока в соленоиде.
ОСНОВНЫЕ ВЫВОДЫ
1.Вокруг проводника с электрическим током, возникает магнитное поле. Это поле обнаруживается по действию на проводник с током, вносимый в это поле.
2.Для исследования магнитного поля используются пробные контуры, т.е.
замкнутые контуры, по которым течёт постоянный ток, внесение которых не искажает исследуемого поля. Пробный контур характеризуют магнитным моментом pm , который является вектором. Его модуль равен pm = IS, где I —
сила тока в контуре, S — площадь контура. Вектор pm направлен перпендику-
лярно к плоскости контура и связан с направлением тока правилом правого винта: при вращении винта в направлении тока его поступательное движение показывает направление магнитного момента контура.
3. Магнитные поля характеризуют индукцией B магнитного поля. Его модуль равен B = Mmax /pm, где Mmax — максимальный момент сил, действую-
щих на пробный контур. Направление B совпадает с направлением prm конту-
ра, находящегося в положении, когда на него не действует момент сил. Индукция магнитного поля измеряется в теслах.
4. Для наглядного изображения магнитного поля пользуются линиями маг-
нитной индукции, т.е. линиями, в каждой точке которой вектор индукции магнитного поляr направлен по касательной. По густоте этих линий судят о мо-
дуле вектора B.
5. На участок проводника с током длиной dl действует сила, модуль dF которой равен: dF = B I dl sinα. Здесь B — модуль индукции магнитного поля, I — сила
тока, α — угол между направлениями тока и вектора B. Направление силы находится по правилу левой руки. Это соотношение носит название закона Ам6пера. М .гнитное поле в веществе, называемым магнетиком, определяется внешним полем, в которое оно внесено, и собственным магнитным полем, создаваемым атомами вещества. Если направления этих полей совпадают, то поле внутри магнетика усиливается, если же противоположно — ослабляется. Существует три вида магнетиков: диа−, пара− и ферромагнетики. В диамагнетиках поле ослабляется, а в парамагнетиках незначительно усиливается. Это группа слабо магнитных материалов. Ферромагнетики — это вещества с сильными магнитными свойствами, которые обусловлены наличием в них областей, называемых доменами, с самопроизвольной ориентацией спиновых магнитных моментов электронов.
7. Усиление или ослабление магнитного поля в веществе характеризуют магнитной проницаемостью μ, которая показывает, во сколько раз модуль B индук-
ции магнитного поля в веществе отличается от модуля Bυ индукции магнитного поля в вакууме, т.е. μ = B/Bυ.
60

8. Любое магнитное поле можно рассчитывать, используя закон Био − Савара
− Лапласа: dB = μ0μ I dl 2sinα. Здесь μ0 — магнитная постоянная, μ — маг- 4π r
нитная проницаемость среды, окружающей проводник, по которому течёт ток силой I, dB — модуль индукции магнитного поля, создаваемого элементарным участком проводника с током длиною dl, r — модуль радиус-вектора, проведённого от dl в точку, в которой определяется поле, α — угол между направлением тока и вектором rr. Направление dB находится по правилу правого винта, оно перпендикулярно к плоскости, проведённой через dl и r (см. рис. 25.1). Используя закон Био − Савара − Лапласа, рассчитывают магнитное поле прямого и кругового токов (см. формулы (25.8) и (25.9)).
9. В ряде случаев расчёт магнитных полей упрощается при использовании зако-
на полного тока: циркуляция индукции магнитного поля по произвольному замкнутому контуру равна произведению магнитной постоянной μ0, магнитной проницаемости μ на алгебраическую сумму токов, охватываемых этим контуром:
r |
r |
n |
∫B dl |
= μ0μ ∑Ik . Отличие от нуля циркуляции вектора B свидетельствует о вих- |
|
l |
|
k =1 |
ревомхарактеремагнитногополя. r
10. Существуют два вида полей — потенциальные и вихревые. Если ∫G dl = 0,
l
то поле называют потенциальнымr r . Таковыми являются электростатические и гравитационные поля. Если ∫G dl ≠ 0, то поле называется вихревым. К нему относятся
l
постоянное магнитное поле и переменное электрическое поле. Здесь G — напряженность(индукция) полей.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Дайте понятие индукции магнитного поля.
2.Сформулируйте и запишите закон Ампера.
3.Что называется линиями магнитной индукции? Для чего они применяются.
4.Что называют орбитальным и спиновым магнитным моментом электрона?
5.Из чего складывается магнитный момент атома?
6.Усиливается или ослабляется магнитное поле в диа− и парамагнетиках? В чём причина этого?
7.Почему магнитное поле в ферромагнетиках сильно увеличивается при внесении их в магнитное поле?
8.Что характеризует магнитная проницаемость вещества?
9.В чём смысл закона Био – Савара – Лапласа и как он записывается?
10.Рассчитайте магнитное поле прямого и кругового токов.
11.Сформулируйте и запишите закон полного тока.
12.Определите индукцию магнитного поля бесконечно длинного соленоида.
13.Что такое потенциальное и вихревое поле?
61
ЗАДАЧИ
3.1.Определить индукцию магнитного поля в центре кругового проволочного витка радиусом 2 см, по которому протекает ток силой 2 А.
3.2.Найти индукцию магнитного поля на оси кругового контура на расстоянии 5 см от его плоскости. Радиус контура 2 см, сила тока в контуре 3 А.
3.3.Индукция магнитного поля в центре кругового витка 2 мТл. Радиус витка 10 см. Найти индукцию магнитного поля на оси витка на расстоянии 10 см от его плоскости.
3.4.Ток силой в 30 А идёт по длинному проводнику, согнутому под прямым углом. Найти индукцию магнитного поля в точке, лежащей на биссектрисе этого угла и отстоящей от вершины угла на расстоянии 15 см.
3.5.Из проволоки длиною 1 м сделана квадратная рамка. По этой рамке течёт ток силой 20 А. Найти индукцию магнитного поля в центре рамки.
3.6.Два прямолинейных длинных проводника расположены параллельно на расстоянии 10 см друг от друга. По проводникам текут одинаковые токи силой 5 А в противоположных направлениях. Найти индукцию магнитного поля в точке, удалённой от каждого проводника на 10 см.
3.7.Два круговых витка радиусом 4 см каждый расположены в параллельных плоскостях на расстоянии 5 см друг от друга. По виткам текут одинаковые токи в одном направлении силой 4 А. Найти индукцию магнитного поля в центре каждого витка.
3.8.Ток силой 25 А, протекая по проволочному кольцу из медной проволоки сечением 2 мм2, создаёт в центре кольца индукцию магнитного поля 50 мТл. Какая разность потенциалов
приложена к концам проволоки, образующей кольцо. Удельное сопротивление меди
1,7 10–8 Ом м.
3.9.Обмотка соленоида сделана из проволоки диаметром 0,8 мм. Витки плотно прилегают друг к другу. Считая соленоид достаточно длинным, найти индукцию магнитного поля внутри него при силе тока 2 А.
3.10.Два прямолинейных длинных параллельных проводника находятся на расстоянии 10 см друг от друга. По проводникам в одном направлении текут токи силой 20 и 30 А. Какую работу надо совершить (на единицу длины проводников), чтобы раздвинуть их до расстояния 20 см.
3.11.Найти кинетическую энергию протона, движущегося по дуге окружности радиусом 50 см в однородном магнитном поле с индукцией 30 мкТл.
3.12.Электрон влетает в однородное магнитное поле с индукцией 10 мкТл под углом 30° к направлению поля и движется по винтовой линии, радиус которой 1 см. Найти кинетическую энергию электрона.
ГЛАВА 4. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
§29. МАГНИТНЫЙ ПОТОК. ТЕОРЕМА ГАУССА ДЛЯ МАГНИТНОГО ПОЛЯ
1. По аналогии с потоком напряжённости электрического поля (см. §6, п. 1) вводится поток индукции магнитного поля или магнитный поток. Магнитным потоком через некоторую поверхность называют число линий магнитной ин-
дукции, пронизывающих её. Пусть в неоднородном магнитном поле находится поверхность площадью S. Для нахождения магнитного потока через неё мысленно разделим поверхность на элементарные участки площадью dS, которые можно считать плоскими, а поле в их пределах однородным (рис. 29.1). Тогда элементар-
62
