
учебник , электродинамика
.pdfЧАСТЬ 1. ЭЛЕКТРОДИНАМИКА
Электродинамика это учение об электрических и магнитных явлениях. Электромагнитные взаимодействия, которые изучает электродинамика, ответственны за большинство явлений, например, за образование атомов и молекул, из которых состоят тела. Силы Ван−дер−Ваальса, химические связи и т. д. всё это проявление электромагнитных взаимодействий. Можно сказать, что электродинамика объясняет не только электрические и магнитные явления, но и те силы, вследствие которых вещество существует как целое. Поскольку молекулярные силы имеют электромагнитную природу, то почти все биологические явления определяются электромагнетизмом. Силы в повседневной жизни также имеют электромагнитный характер, хотя мы их классифицируем как мускульные, упругие и т. д.
С электромагнитными явлениями сталкиваются во многих разделах физики и прежде всего в оптике, атомной и ядерной физике. Свет, тепловое, ультрафиолетовое и рентгеновское излучения есть проявление электромагнитных колебаний. Радио и телевидение используют электромагнитные волны для передачи информации на расстояния. Таким образом, можно сказать, что учение об электричестве имеет глубиннуювзаимосвязьсомногимифизическимипроцессами.
Не менее важен другой аспект электродинамики, заключающийся в том, что данный раздел физики является основой для изучения таких технических дисциплин как электротехника, радиотехника, автоматика и т. д. В основе работы электростанций, радиопередающих и принимающих устройств, большого количества измерительных приборов, лазеров, вычислительных машин лежат законы электродинамики.
Электродинамику как раздел физики условно можно разделить на три части: электростатику, учение об электрическом токе и электромагнетизм. Начнём изучение электродинамики с раздела электростатика, прежде всего потому, что в нём вводится ряд понятий таких, как заряд, электрическое поле, напряжённость и потенциал поля, электроёмкость и т. д., которые широко используются в электродинамике и электронике.
ГЛАВА 1. ЭЛЕКТРОСТАТИКА
Электростатика это раздел электродинамики, изучающий свойства неподвижных зарядов, их взаимодействия друг с другом посредством полей, называемых электростатическими. Условие неподвижности зарядов в той системе отсчёта, в которой они изучаются, является весьма важным, так как в случае движущихся зарядов свойства окружающего пространства кардинально меняются и, в частности, появляется магнитное поле.
3
§1. ЭЛЕКТРИЧЕСКИЙ ЗАРЯД. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА. ЗАКОН КУЛОНА
1. Известно, что разнородные тела такие, как кожа, стекло, эбонит и т.д., потёртые друг о друга, обладают свойством притягивать к себе лёгкие предметы, например, кусочки бумаги. Для объяснения такого взаимодействия, названного электрическим, и было введено понятие электрического заряда. Заряженные тела могут, как притягиваться, так и отталкиваться друг от друга. Этот факт можно объяснить, если ввести два типа заряда, условно названных положительными и отрицательными (плюс и минус). Как следует из опыта, заряды с одинаковыми знаками отталкиваются, а с разными притягиваются. Сила взаимодействия заряженных тел может быть различной. Она зависит от величины зарядов, находя-
щихся на них. Из этого следует вывод: электрический заряд является количе-
ственной мерой способности тел к электрическим взаимодействиям.
Заряд тела не зависит от выбора системы отсчёта, т.е. не зависит от того, движется или покоится тело, на котором он находится. Следовательно, электрический заряд является релятивистски-инвариантной величиной в отличие от массы тела (см. § 29, т. 1).
В системе единиц СИ заряд измеряется в кулонах (Кл). 1 Кл равен заряду,
протекающему через поперечное сечение проводника за 1 с при силе постоян-
ного тока в 1 A (определение единицы силы тока 1 A см. в §26).
2. Возникновение зарядов на телах обусловлено следующим. Все тела построены из атомов. Атом состоит из положительно заряженного ядра и отрицательно заряженных электронов. Заряд ядра обусловлен протонами. Заряды протона и электрона равны по абсолютной величине, но противоположны по знаку. Число протонов и электронов в атоме одинаково. Поэтому атом в целом нейтрален, т.е. алгебраическая сумма зарядов атома (сумма зарядов с учётом знаков) равна нулю, а следовательно, и тело нейтрально. Чтобы зарядить тела, т.е. наэлектризовать их, надо отделить часть отрицательного заряда от связанного с ним положительного. Тело, на котором оказывается избыток электронов по сравнению с протонами, заряжается отрицательно, если наоборот положительно. Например, при электризации трением небольшая часть электронов с одного тела переходит на другое. Если теперь раздвинуть тела, то они окажутся заряженными одно положительно, другое отрицательно.
3. Из обобщения опытных данных установлен закон сохранения электриче-
ского заряда: в любой замкнутой электрической системе алгебраическая
сумма электрических зарядов является постоянной величиной при любых процессах, происходящих в ней.
Замкнутой называется электрическая система, из которой не выходят и в которую не входят заряды. Так, при электризации тел трением заряды, возникающие на телах, равны по абсолютной величине, но противоположны по знаку. Поэтому их алгебраическая сумма так же равна нулю, как и в случае незаряженных тел.
4

q rr q0 Fr 4. Рассмотрим вопрос о силе взаимодей-
|
ствия электрических зарядов, которая опре- |
|
|
деляется законом Кулона, являющимся ос- |
|
Рис. 1.1 |
новным законом электростатики. Этот закон |
|
не выводится из других законов природы и |
||
|
||
устанавливается только опытным путём. |
||
В общем случае сила взаимодействия между заряженными телами зависит от размеров и формы тел, а также от свойств среды, в которой находятся тела. Наиболее просто сила взаимодействия находится для так называемых точечных зарядов. Точечным зарядом называется заряженное тело, размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми оно взаимодействует. Закон взаимодействия точечных зарядов был открыт Кулоном и формулируется следующим образом: модуль F силы взаи-
модействия между двумя неподвижными зарядами q и q0 пропорционален
произведению этих зарядов, обратно пропорционален квадрату расстояния r между ними, т.е.
|
|
|
|
|
|
|
|
|
|
F = |
1 |
|
|
qq0 |
, |
|
(1.1) |
|
|
|
||||||
|
4πε |
0 |
|
εr 2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где ε0 электрическая постоянная, ε — диэлектрическая проницаемость, характеризующая среду (см. §5, п. 5). Эта сила направлена вдоль прямой линии, соединяющей заряды. Электрическая постояннаяравнаε0 = 8,85 10–12 Кл2/(Нм2) или ε0 = 8,85 10–12
Ф/м, где фарад (Ф) единица электроёмкости (см. §12). Закон Кулона более строго следует записать в векторном виде, поскольку сила является вектором. С этой целью проведём радиус-вектор r от заряда q к q0 (рис. 1.1). Введём еди-
ничный вектор, направленный в ту же сторону, что и вектор rr. Он равен r /r. Тогда закон Кулона в векторной форме запишется
|
Fr = |
1 |
|
|
qq0 |
|
rr |
. |
|
(1.2) |
|
|
|
||||||||
|
|
|
|
|||||||
|
4πε |
0 |
|
εr 2 |
r |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§2. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ. НАПРЯЖЁННОСТЬ ПОЛЯ
1. Напряжённость. Ранее (см. §17, т. 1) для объяснения притяжения тел было введено понятие гравитационного поля. Это поле создаётся массой. В случае заряженных тел их электрическое взаимодействие легко объясняется, если предположить, что вокруг заряженных тел существует электрическое поле. Электрическое поле, создаваемое одним заряженным телом, действует на другое заряженное тело и наоборот. Для характеристики электрического поля, как и в случае гравитационного поля, вводится физическая величина, называемая
5
напряжённостью, которая является силовой характеристикой этого поля. Изучение электрического поля производится с помощью пробного заряда, т.е. положительного точечного заряда, при внесении которого исследуемое поле не искажается. Если в одну и ту же точку поля вносить различные пробные заря-
ды, то на них будут действовать и различные силы. Однако отношение силы F , действующей на заряд, к величине q0 этого заряда является постоянным для
всех вносимых зарядов, независимо от их величины. Поэтому это отношение принимают за характеристику электрического поля в данной точке. Её называют
напряжённостью и обозначают через E . Тогда
r |
F |
|
|
|
E = |
|
. |
(2.1) |
|
q0 |
||||
|
|
|
Поскольку q0 заряд положительный, то из выражения (2.1) вытекает, что напряжён-
ность поля равна силе, которая действует со стороны поля на положительный единичный заряд, и совпадает по направлению с направлением этой силы. В системе единиц СИ, как следует из (2.1), напряжённость измеряется в ньютон/кулон (Н/Кл).
1 Н/Кл= 1 / 1 Кл, т.е. 1 Н/Кл напряжённость в такой точке поля, в которой на заряд в 1 Кл действует сила в 1 Н.
2. Напряжённость поля точечного заряда. Найдём напряжённость E элек-
тростатического поля, создаваемого точечным зарядом q, находящимся в однородном изотропном диэлектрике, в точке, отстоящей от него, на расстоянии r. Мысленно поместим в эту точку пробный заряд q0. Тогда, согласно (2.1) и (1.2),
Er = |
F |
и Fr = |
1 |
|
|
qq0 |
|
rr |
. Отсюда получаем, что |
|
||||||
|
|
|
|
r |
|
|||||||||||
|
q0 |
4πε |
0 |
|
εr 2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
r |
1 |
|
q |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
E = |
|
|
|
|
|
, |
(2.2) |
|
|
|
|
|
|
|
|
|
4πε0 |
εr 2 |
r |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где rr радиус-вектор, проведённый от заряда q к точке, в которой определяется напряжённость поля. Из формулы (2.2) следует, что модуль напряжённости поля
E = |
1 |
|
q |
. |
(2.3) |
|
|
||||
4πε0 |
|
εr 2 |
|
||
Таким образом, модуль напряжённости в любой точке электростатического поля, создаваемого точечным зарядом в вакууме, пропорционален величине заряда и обратно пропорционален квадрату расстояния от заряда до точки, в которой определяется напряжённость.
§3. СУПЕРПОЗИЦИЯ ПОЛЕЙ
6

Знание поля точечного заряда позволяет в принципе рассчитывать поля, создаваемые как совокупностью зарядов, так и протяженными заряженными телами. Для этого в физике используется простой, но очень важный принцип суперпозиции (наложения) полей, суть которого заключается в следующем.
1. Пусть имеется система точечных электрических зарядов q1, q2,..., qn. Най-
дём напряженность электрического поля, создаваемой этими зарядами, в произвольной точке. Мысленно поместим в эту точку пробный заряд q0. Опытным
путём установлено, что сила F , с которой система зарядов действует на этот заряд, равна векторной сумме сил F1, F2 ,..., Fn , с которыми действует на пробный заряд каждый из зарядов системы, т.е. F = F1 + F2 +... + Frn . Разделим это
равенство |
на |
|
заряд q |
0 |
: |
F |
|
= |
Fr |
1 + Fr |
2 +... + Frn |
= |
|
|
Fr1 |
+ |
Fr |
2 |
+ |
... + |
Frn |
. |
Согласно |
||||||||||
|
|
|
|
|
|
|
q0 |
|
|
q0 |
|
|
|
|
|
|
|||||||||||||||||
|
Fr1 |
|
|
|
Fr 2 |
|
|
|
q0 |
|
|
|
|
|
|
|
|
q |
0 |
|
|
q |
0 |
|
|
||||||||
(2.1), |
r |
|
, |
r |
|
,..., |
Frn |
|
r |
|
напряжённость |
электрических полей, |
|||||||||||||||||||||
|
|
= E |
1 |
|
= E |
2 |
|
|
|
= E |
n |
||||||||||||||||||||||
q0 |
q0 |
|
q0 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
r |
|
|
|
|
|
||
создаваемых отдельными зарядами в данной точке, а |
|
|
|
|
= E |
напряжённость |
|||||||||||||||||||||||||||
|
q0 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
электрического поля системы зарядов в той же точке. Поэтому |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Er = E1 + E2 +... + En , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.1) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
т.е. напряжённость поля системы зарядов равна векторной сумме напряжённостей полей, которые создаёт каждый заряд системы в отдельности. Соотношение (3.1) называют принципом суперпозиции полей.
2. Для нахождения напряжённости электростатического поля, создаваемого заряженным протяжённым телом в некоторой точке, тело мысленно разбивают на элементарные части с зарядом dq, которые можно принять за точечные заряды. Тогда элементарную напряжённость dE в этой же точке находим по формуле
|
r |
1 |
|
dq |
|
r |
|
|
|
|
|
|
|
|
|
(2.2) |
dE = |
|
|
|
|
|
. Используя принцип суперпозиции полей, напряжённость |
||||||||
4πε0 |
εr 2 |
r |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Er поля в данной точке будет равна: |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
Er = ∫dEr = ∫ |
1 |
|
r |
|
dq, |
(3.2) |
||
|
|
|
|
|
|
|
4πε0 |
εr3 |
|||||||
|
|
|
|
|
|
|
V |
V |
|
|
|
||||
где V — объём тела, поскольку суммирование элементарных величин означает интегрирование.
§4. ЛИНИИ НАПРЯЖЁННОСТИ
7

Очевидно, что напряжённость в каждой точке электрического поля имеет определённую величину и направление. Для наглядного изображения электриче-
ского поля пользуются линиями напряжённости или силовыми линиями, т.е.
линиями, в каждой точке которых вектор напряжённости электрического поля направлен по касательной к ним. Наиболее просто это можно уяснить на при-
мере однородного электростатического поля, т.е. поля, в каждой точке кото-
рого напряжённость одинакова по модулю и направлению. В этом случае линии напряжённости проводятся так, чтобы число линий ФЕ, проходящих через единицу площади плоской площадки S, расположенной перпендикулярно к этим
E1 |
E2 |
r |
|
|
E3 |
E |
|||
|
||||
E |
|
|
E4 |
Рис. 4.1 |
Рис. 4.2 |
линиям, равнялось бы модулю E напряжённости этого поля, т.е. |
|
E = ФE . |
(4.1) |
S |
|
Вид линий напряженности однородного электростатического поля показан на рис. 4.1. Они представляют собой параллельные линии, отстоящие друг от друга на одинаковом расстоянии. Если поле неоднородное, то надо выбрать элементарную площадку dS, перпендикулярную к линиям напряжённости, в пределах которой напряжённостьполяможносчитатьпостоянной. Тогда, согласно(4.1), запишем:
E = |
dФE |
, |
(4.2) |
|
|||
|
dS |
|
|
где dФE число линий напряжённости, пронизывающих эту площадку, т.е. мо-
дуль напряжённости электрического поля равен числу линий напряжённости, приходящихся на единицу площади площадки, перпендикулярной к ней. При таком способе построения по густоте линий напряжённости судят о модуле напряжённости электрического поля в различных точках поля. Там, где линии расположены гуще, модуль напряжённости поля больше. Следует отметить, что линии напряжённости никогда не пересекаются, поскольку их пересечение означало бы
отсутствие определённого направления вектора E в точках их пересечения. Картина линий напряжённости для неоднородного электростатического поля приведена на рис. 4.2. Из этого рисунка видно, что Е4 < E3 < E2 < E1. Об этом можно судить по густоте линий. Условились считать, что линии напряжённости начинаются на положительных зарядах и оканчиваются на отрицательных.
8
§5. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКАХ
Диэлектрики — это вещества, не проводящие электрический ток. Диэлектрик (как и любое вещество) состоит из атомов или молекул, которые построены из ядер и электронов. Размеры атомных ядер и электронов примерно в 105 раз меньше размеров самих атомов. Поэтому объём заряженных частиц, находящихся в некотором теле, ничтожно мал по сравнению с объёмом тела. Это позволяет представить тело как часть вакуумного пространства, в котором вкраплены заряженные частицы. При этом напряжённость поля в нём, согласно принципу суперпозиции полей, складывается из напряжённости внешнего поля и напряжённости электрических полей, создаваемых заряженными частицами тела в вакууме. Возникает вопрос, как можно рассчитать напряжённость поля внутри диэлектрика? Для этого рассмотрим вначале понятие электрического диполя и поведение отдельных молекул в электрическом поле.
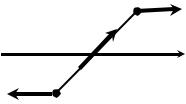
1. Электрический диполь. Электрическая система, состоящая из двух равных по абсолютной величине и противоположных по знаку точечных зарядов, отстоящих друг от друга на некотором расстоянии, называется электрическим диполем. Вокруг диполя существует электрическое поле, зависящее от так называемого дипольного момента. Дипольный момент является вектором, направленным от отрицательного заряда к положительному заряду (рис. 5.1). Его модуль pe рассчитывается по формуле: pe = ql, где q заряд по абсолютной
величине, l расстояние между зарядами.
2.Полярные молекулы. Установлено, что молекулы, в которых электрические заряды распределены не симметрично, обладают дипольным моментом. Поэтому их можно рассматривать как диполи. При этом считают, что весь положительный заряд молекулы как бы сосредоточен в одной точке, которую называют центром положительных зарядов. Аналогично вводится центр отрицательных зарядов. Молекулы, обладающие дипольным моментом в отсутствие внешнего электрического поля, называются полярными молекулами, а диэлектрик, состоящий из них, также называют полярным. К таким диэлектрикам относятся вода, кислоты, основания и другие вещества. При внесении полярного диэлектрика в электростатическое поле его молекулы стремятся ориентироваться так, чтобы их дипольные моменты были направлены вдоль поля. Это происходит под действием сил, приложенных к положительному и отрицательному зарядам диполя, которые приводят к его повороту (рис. 5.1).
3.Неполярные молекулы. Существуют и молекулы, дипольный момент ко-
торых в отсутствие внешнего электрического поля, равен нулю. Их называют |
||||
+q |
F |
неполярными молекулами, а диэлектрик, состоящий |
||
r |
||||
pe |
|
из таких молекул неполярным. Под действием |
||
–q |
E |
электрического поля неполярная молекула приобре- |
||
тает дипольный момент, направленный вдоль поля, |
||||
F |
|
который |
называют наведённым. Это |
обусловлено |
|
тем, что |
силы электрического поля |
деформируют |
|
Рис. 5.1 |
|
|||
9
электронную оболочку молекулы. В результате этого центры отрицательных и положительных зарядов смещаются в противоположные стороны. При снятии поля молекула возвращается в исходное состояние, и наведённый дипольный момент обращается в ноль. Неполярными диэлектриками являются парафин, бензол, азот, водород, кислород и т.д.
– |
+ – |
+ – |
+ – |
+ – |
+ – |
+ – |
+ – |
+ |
|
|
– |
+ – |
+ – |
+ – |
+ – |
+ – |
+ – |
+ – |
+ |
|
|
– |
+ – |
+ |
– |
+ – |
+ – |
+ – |
+ – |
+ – |
+ |
Eυ |
– + – |
+ – |
+ – |
+ – |
+ – |
+ – + – |
+ |
||||
– |
+ – |
+ – |
+ – |
+ – |
+ – |
+ – |
+ – |
+ |
|
|
– |
+ – |
+ – |
+ – |
+ – |
+ – |
+ – |
+ – |
+ |
|
|
– |
+ – |
+ – |
+ – |
+ – |
+ – |
+ – |
+ – |
+ |
|
|
– |
+ – |
+ |
– |
+ – |
+ – |
+ – |
+ – |
+ – |
+ |
|
Рис. 5.2
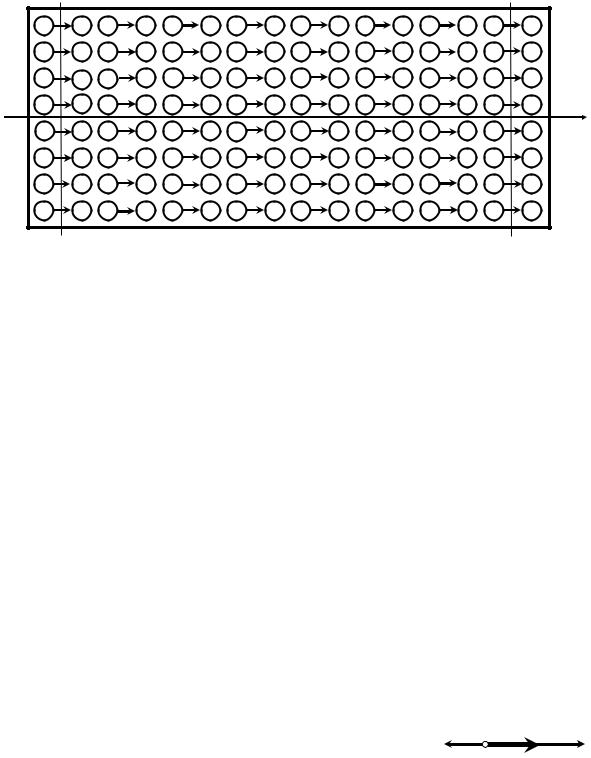
4. Поляризация диэлектриков. В отсутствие электрического поля алгебраическая сумма электрических зарядов в любом выделенном объёме диэлектрика равна нулю. Если диэлектрик поместить во внешнее электростатическое поле, то в полярном диэлектрике дипольные моменты молекул стремятся установиться по полю, а в неполярном — молекулы приобретают наведённый дипольный момент, направленный также вдоль поля (рис. 5.2, где показано сечение диэлектрика, имеющего форму прямоугольного параллелепипеда). Это приводит к возникновению на гранях положительного и отрицательного зарядов, поскольку внутри диэлектрика заряды скомпенсированы (область между пунктирными линиями). Эти не скомпенсированные заряды называются связанными. Явление возникно-
вения связанных электрических зарядов на диэлектрике при внесении его в электрическое поле получило название поляризации диэлектриков.
5. Диэлектрическая проницаемость. Связанные заряды, возникшие на противоположных гранях диэлектрика, создают внутри него собственное электростатическое поле, направленное от положительных зарядов к отрицательным зарядам (рисr . 5.3). Обозначим напряжённостьr внешнего поля, созданного в вакууме, через
Eυ, а собственного — через Ec . Напряжённость E поля в диэлектрике, согласно принципу суперпозиции полей (3.1), равна E = Eυ + Ec или в скалярной форме
E = Eυ − Ec , поскольку векторы Eυ и Ec направле- |
|
|
|
– |
|
Eυ+ |
|
ны противоположно. Следовательно, поле ослабля- |
|
||
ется. Для характеристики ослабления поля в диэлек- |
– |
|
+ |
трике вводится физическая величина, называемая |
– Ec |
E |
+ |
диэлектрической проницаемостью, которая пока- |
|
Рис. 5.3 |
|
|
|
|
10
зывает, во сколько раз модуль Eυ напряжённости электрического поля в вакууме больше модуля E напряжённости того же поля в диэлектрике, т.е.
ε = |
E υ |
. |
(5.1) |
|
|||
|
E |
|
|
§6. ПОТОК НАПРЯЖЁННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. ТЕОРЕМА ГАУССА ДЛЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
1. Потоком напряжённости электрического поля через какую-либо по-
верхность называют число линий напряженности ФE , пронизывающих её. В
случае однородного электростатического поля, когда площадка S перпендикулярна к линиям напряженности, поток ФE напряжённости определяется из
формулы (4.1), как
ФE = ES. |
(6.1) |
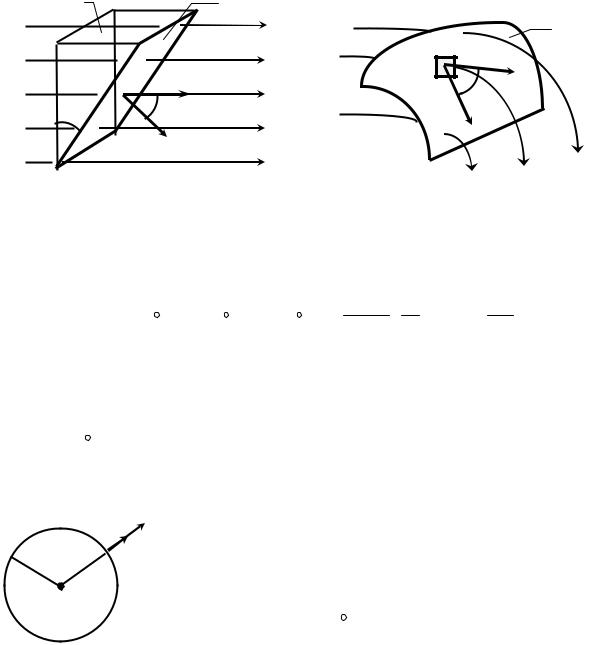
Рассмотрим теперь случай, когда в однородном электростатическом поле находится плоская площадка, имеющая форму прямоугольника со сторонами a и b, площадь которой S = ab. Нормаль n к площадке составляет угол α с направлени-
ем поля, т.е. с вектором напряжённости E (рис. 6.1 а). Число линий напряжённости, проходящих через площадку S и её проекцию Sпр на плоскость, перпендику-
лярную к этим линиям, одинаково. Следовательно, поток ФE напряжённости электрического поля через них одинаков. Используя выражение (6.1), находим, что ФE = ESnp. Из рис. 6.1 а видно, что Sпр = ab cosα = S cosα. Поэтому
ФЕ = ES cos α = En S, |
(6.2) |
где E cos α = En проекция вектора E на направление нормали nr к площадке.
Для вычисления потока ФЕ напряжённости электрического поля через произвольную поверхность S, помещённую в неоднородное электрическое поле (рис. 6.1 б), надо мысленно разбить его на элементарные участки dS, чтобы площадку можно было бы считать плоской, а поле в её пределах однородным. Тогда, согласно (6.2), элементарный поток dФE = En dS, а поток напряжённости электри-
ческого поля через всю поверхность равен сумме этих потоков dФE, т.е.
ФE = ∫E n dS, |
(6.3) |
S |
|
поскольку суммированиеr бесконечно малых величин означает интегрирование. Поток вектора E являетсяr алгебраической величиной, его знак определяется углом между векторами E и nr. Если угол острый, то поток положительный, если же тупой отрицательный. При α = 90° поток равен нулю, так как cos 90° = 0 (см. (6.2)). Выбор направления нормали n произволен. В случае же замкнутой поверхности проводится внешняя нормаль, т.е. нормаль, направлен-
11
ная в наружную область, охватываемой поверхностью. Тогда поток, входящий в объём, будет отрицательным, а выходящий положительным.
2. Понятие потока напряжённости электрического поля используется в теореме Гаусса, которая широко применяется для расчёта напряжённостей электрических полей. Рассмотрим такой поток, создаваемый полем точечного заряда, через замкнутую поверхность, окружающую этот заряд. Мысленно проведём вокруг него сферу произвольного радиуса r с центром в точке расположения заряда (рис. 6.2, на котором приведено сечение сферы плоскостью чертежа
— пунктирная линия). Найдём поток напряжённости электростатическогоr поля через эту поверхность. В данном случае направления векторов E и nr в любой точке поверхности совпадают. Поэтому En = E cos 0° = E. Модуль напряжённо-
Snp |
S |
a) |
S б) |
|
|
dS |
|
|
|
|
|
b |
Er |
α |
E |
α |
|
E |
nr |
α |
r |
|
|
|
|
||
a |
n |
|
r |
|
|
|
E |
|
|
Рис. 6.1 |
|
сти во всех точках на поверхности сферы одинаков и, согласно (69.3), равен
E = |
1 |
|
|
q |
|
C учётом этого из (6.3) получаем: |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||
4πε |
0 |
|
εr 2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
1 |
q |
|
q |
|
|
|
|
|
|
|
|
Ф |
E |
= ∫E |
n |
dS = ∫EdS = E ∫dS = |
4πr 2 = |
, |
(6.4) |
||||
|
|
|
|
|
|
S |
S |
S |
4πε0ε |
r 2 |
|
ε0ε |
|
|
||
где значок ° на интеграле означает, что интегрирование производится по замк-
нутой поверхности. E вынесена за знак интеграла, поскольку она не зависит от S. Суммирование же всех площадей элементарных площадок даёт площадь S сферы, т.е. ∫dS = S = 4πr 2.
S
В теоретической физике доказывается, что соотношение (6.4) справедливо не только для сферы, но и для любой замкнутой поверхности. Если имеется система точечных зарядов, то очевидно, что полный поток
r |
nr E ФЕ напряжённости электрического поля через замкнутую |
||
|
поверхность в силу принципа суперпозиции полей равен |
||
О |
сумме потоков ФЕi, создаваемых каждым зарядом qi в от- |
||
дельности, т.е. ФE = ∫E n dS = |
∑ФEi . Но, как следует из |
||
|
|||
|
S |
i |
|
Рис. 6.2 |
(6.4), ФEi = qi / (ε0ε). Поэтому |
|
|
12
