КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНОСТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

Кафедра физики

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ПО ФИЗИКЕ.

ЭЛЕКТРОМАГНЕТИЗМ. КОЛЕБАНИЯ И ВОЛНЫ

для студентов специальностей

2903, 2906, 2907, 2908, 2910

Казань

2005

ЭЛЕКТРОМАГНЕТИЗМ

Напряженность магнитного поля в центре кругового тока

H = 2IR ,

где R — радиус кругового контура с током, I — сила тока в проводнике. Напряженность магнитного поля, созданного бесконечно длинным прямолинейным проводником

H = 2πI a ,

где a — расстояние от точки, где находится напряженность, до проводника с током;

Напряженность магнитного поля на оси кругового тока

где R — радиус кругового контура с током и a - расстояние от точки, где находится напряженность, до плоскости контура.

Напряженность магнитного поля внутри тороида и бесконечно длинного соленоида

H = I n ,

где n — число витков на единицу длины соленоида (тороида). Индукция магнитного поля B связана с напряженностью H соотношением

B =μμ0 H ,

где μ — магнитная проницаемость среды и μ0 — магнитная постоянная, равная μ0 = 4π 10−7 Гн/м.

Поток магнитной индукции через контур

Ф = BS cosα,

где S — площадь поперечного сечения контура, α — угол между нормалью к

плоскости контура и направлением магнитного поля.

На элемент dl проводника с током, находящийся в магнитном поле, действует сила Ампера, равная

dF = B I dl sinα ,

где α — угол между направлением тока и магнитного поля.

3

На замкнутый контур с током, а также на магнитную стрелку в магнитном поле, действует пара сил с вращающим моментом

M = p B sinα,

где p — магнитный момент контура с током и α — угол между направлением

магнитного поля и нормалью к плоскости контура. Магнитный момент контура с током

p = I S ,

где S — площадь контура, так что

M = I B S sin α.

Два параллельных прямолинейных проводника с токами I1 и I2 взаимодействуют между собой с силой:

F = μμ0 I1I2l ,

2πd

где l — длина проводников и d — расстояние между ними. Работа перемещения проводника с током в магнитном поле

dA = I dΦ,

где dФ — магнитный поток, пересеченный проводником при его движении. Сила, действующая на заряженную частицу, движущуюся со скоростью V в магнитном поле, определяется формулой Лоренца

F = B q V sinα ,

где q — заряд частицы и α — угол между направлением скорости

положительно заряженной частицы и магнитного поля. Явление электромагнитной индукции заключается в появлении в контуре Э.Д.С. индукции при всяком изменении потока магнитной индукции сквозь

поверхность, охватываемую контуром. Величина Э.Д.С. индукции определяется законом Фарадея

εi = −ddtΦ .

Изменение потока магнитной индукции может достигаться изменением силы тока в самом контуре (явление самоиндукции). При этом Э.Д.С. самоиндукции определяется формулой

εi = −L dIdt ,

где L — индуктивность контура.

4

ускорение свободного падения.

Для электрических колебаний в контуре, состоящем из емкости C и

индуктивности L, период колебаний будет равен

T = 2π LC .

При сложении двух одинаково направленных гармонических колебаний одинакового периода получается гармоническое колебание того же периода с амплитудой

A = A12 + A22 + 2A1 A2 cos(ϕ2 −ϕ1 )

и с начальной фазой, определяемой из уравнения

tgϕ= A1 sinϕ1 + A2 sinϕ2 , A1 cosϕ1 + A2 cosϕ2

где A1 и A2 — амплитуды складываемых колебаний, ϕ1 и ϕ2 — их начальные

фазы.

При сложении двух взаимно перпендикулярных колебаний одинакового периода уравнение траектории результирующего движения имеет вид

Если на материальную точку в механической колебательной системе, кроме упругой силы действует еще сила трения F = –rV, где r — коэффициент трения и V — скорость колеблющейся точки, то колебания будут затухающими. Уравнение затухающего колебательного движения имеет вид

x = A e−βt cos( ωt +ϕ).

Здесь β = r/2m — коэффициент затухания, а ω= ω02 −β2 , где

ω0 — циклическая частота собственных колебаний (частота колебаний

системы без потерь энергии).

Величина =βT называется логарифмическим декрементом затухания.

Если на материальную точку массой m, колебание которой дано в виде x = A e−βt cos ωt , действует внешняя периодическая сила F = F0 cos Ωt , то

колебании точки будут вынужденными и уравнение ее движения примет вид

тогда, когда частота вынужденных колебаний Ω связана с частотой

6

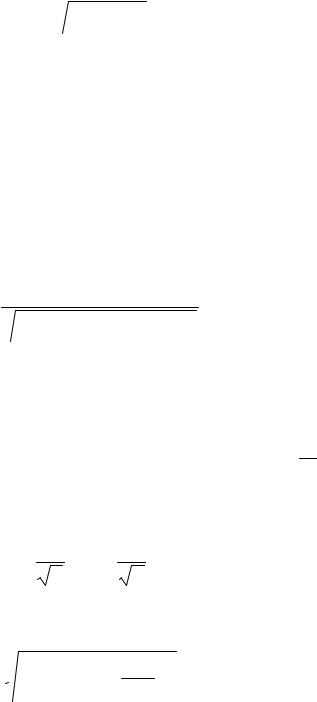
собственных колебаний ω0 и с коэффициентом затухания δ соотношением

Ωp = 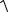ω02 −2β2 .

Для электрического колебательного контура колебания будут затухающими если в LC контур включить сопротивление R. Напряжение на конденсаторе будет меняться по закону

U =U0 e−βt cos ωt .

Здесь β = R / 2L . Если в колебательный контур последовательно включить внешний генератор с периодически меняющимся напряжением U =U0 cos Ωt

будем иметь дело с вынужденными колебаниями той же частоты . Для амплитуды (максимального значения напряжения на конденсаторе) вынужденных колебаний будет выполняться следующее выражение

U ω2

Uco = 0 0 .

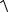( ω02 −Ω2 )2 +4β2Ω2

ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК

Закон Ома для переменного тока записывается в виде I =UZ , где

I и U — эффективные значения тока и напряжения, связанные с их амплитудными значениями I0 и U0 соотношениями

I= I02 ,U = U20 ,

аZ — полное сопротивление цепи. Если цепь содержит сопротивление R, емкость C и индуктивность L, соединенные последовательно, то

Z = R2 +( ΩL − Ω1C )2 .

При этом сдвиг фаз между напряжением и током определяется формулой

Катушка, обладающая сопротивлением R и индуктивностью L, в цепи переменного тока соответствует последовательно включенным R и L. Реальный конденсатор (с потерями энергии) соответствует параллельно включенным R и C.

7

Мощность переменного тока P = I U cos ϕ

ВОЛНЫ

При распространении незатухающих колебаний со скоростью с вдоль некоторого направления, называемого лучом, смещение любой точки, лежащей на луче и отстоящей от источника колебаний на расстоянии l, дается уравнением

x = Asin( 2Tπt − 2λπl ),

где A — амплитуда колеблющихся точек, λ — длина волны. При этом λ = c T . Две точки, лежащие на луче на расстоянии l1 и l2 от источника

колебаний, имеют разность фаз

ϕ2 −ϕ1 = 2πl2 λ−l1 .

При интерференции волн максимум и минимум амплитуды получаются соответственно при условиях

Здесь l2 −l1 — геометрическая разность хода волн.

8

магнитного поля в точке, находящейся на расстоянии a = 10 см от каждого проводника.

8 (11.10)По длинному вертикальному проводнику сверху вниз идет ток I = 8A. На каком расстоянии a от него напряженность поля, получающегося от сложения земного магнитного поля и поля тока, направлена вертикально вверх? Горизонтальная составляющая напряженности земного поля Hг = 16А/м.

9 (11.11) Найти напряженность H магнитного поля, создаваемого отрезком АВ прямолинейного проводника с током, в точке С, расположенной на перпендикуляре к середине этого отрезка на расстоянии a = 5 см от него. По проводнику течет ток I = 20 A. Отрезок АВ проводника виден из точки С под углом 60 градусов.

10 (11.12) Решить предыдущую задачу при условии, что ток в проводнике равен

30 А и отрезок проводника виден из точки С под углом 90°. Точка С расположена на расстоянии 6 см от проводника.

11 (11.15) Ток I = 20 A идет по длинному проводнику, согнутому под прямым углом. Найти напряженность H магнитного поля в точке, лежащей на биссектрисе этого угла и отстоящей от вершины угла на расстоянии a = 10см.

12 (11.16) Ток I = 20 A, протекая по кольцу из медной проволоки сечением

S = 1 мм2, создает в центре кольца напряженность магнитного поля H = 178A/м. Какая разность потенциалов U приложена к концам проволоки, образующей кольцо?

13 (11.17) Найти напряженность H магнитного поля на оси кругового контура на расстоянии a = 3 см от его плоскости. Радиус контура R = 4 см, ток в контуре

I = 2 A.

14 (11.18) Напряженность магнитного поля в центре кругового витка H0 = 64А/м. Радиус витка R = 11 см. Найти напряженность H магнитного поля на оси витка на расстоянии a = 10 см от его плоскости.

15 (11.19) Два круговых витка радиусом R = 4 см каждый расположены в параллельных плоскостях на расстоянии

d = 10 см друг от друга. По виткам текут токи I1 = I2 = 2 A. Найти напряженность H магнитного поля на оси витков в точке, находящейся на равном расстоянии от них. Задачу решить, когда: а) токи в витках текут в одном направлении; б) токи в витках текут в противоположных направлениях.

16 (11.20) Два круговых витка радиусом R = 4 см каждый расположены в параллельных плоскостях на расстоянии d = 5 см друг от друга. По виткам текут токи I1 = I2 = 4 A. Найти напряженность H магнитного поля в центре одного из витков. Задачу решить, когда а) токи в витках текут в одном направлении; б) токи в витках текут в противоположных направлениях.

10