2.5. Метод Зейделя.

Вычисления в этом методе почти такие же, как и в методе Якоби, с той лишь разницей, что в последнем новые значения не используются до новой итерации. В методе Зейделя при нахождении-ой компоненты используются уже найденные компоненты этой же итерации с меньшими номерами, т.е. последовательность итераций задается формулой:

, (2.17)

Сходимость и точность достигаются условиями (2.13) и (2.14).

Пример 2.7. Задать итерационный процесс Зейделя для нахождения решений системы уравнений (2.15).

Решение. Достаточное условие сходимости (2.13) выполняется, поэтому начальное приближение может быть любым.

Используя (2.16) получим:

После задания начального приближения, например, выражение для первой итерации имеет вид:

Результаты первой итерации подставляют в правую часть и получают результаты второй итерации:

Результаты второй итерации подставляют в правую часть и получают результаты третьей итерации:

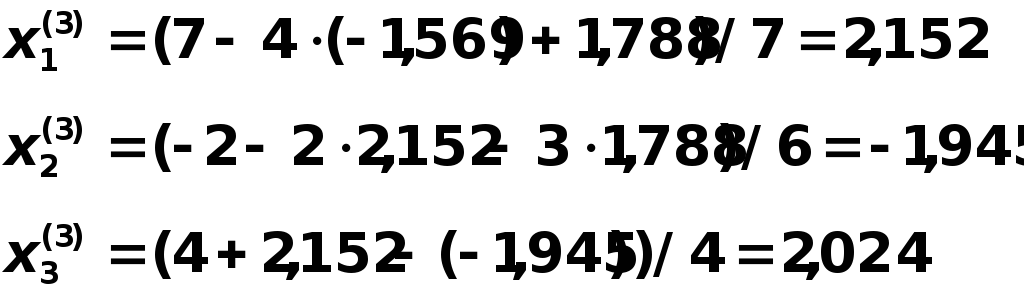
Погрешность решения:

3. Численные методы решения систем нелинейных уравнений.

Требуется решить систему нелинейных уравнений вида:

(3.1)

…

3.1. Метод простой итерации (метод Якоби).

Систему нелинейных уравнений (3.1) после преобразований

,

(здесь определяются из условия сходимости), представим в виде:

(3.2)

…

Из системы (3.2) легко получить итерационные формулы метода Якоби. Возьмем в качестве начального приближения какую-нибудь совокупность чисел . Подставляя их в правую часть (3.2) вместо переменных , получим новое приближение к решению исходной системы:

(3.3)

…

Эта операция получения первого приближения решения системы уравнения (3.2) называется первым шагом итерации. Подставляя полученное решение в правую часть уравнения (3.2) получим следующее итерационное приближение: и т.д.:

, . (3.4)

Итерационный процесс можно считать законченным, если все значения переменных, полученных ()-ой итерации, отличается от значений соответствующих переменных, полученных от предыдущей итерации, по модулю меньше наперед заданной точности , т.е. если:

(3.5)

3.2. Метод Зейделя.

Метод Зейделя отличается от метода Якоби тем, что вычисления ведутся не по формулам (3.4), а по следующим формулам:

(3.6)

…

При решении систем нелинейных уравнений необходимо определить приемлемое начальное приближение. Для случая двух уравнений с двумя неизвестными начальное приближение находится графически.

Сходимость метода Зейделя (Якоби тоже) зависит от вида функции в (3.2), вернее она зависит от матрицы, составленной из частных производных:

, (3.7)

где .

Итерационный процесс сходится, если сумма модулей каждой строки меньше единицы в некоторой окрестности корня:

,

или

Пример 3.1. Найти решение системы методом Зейделя с точностью :

(3.8)

Решение: Представим (3.8) в виде (3.5):

(3.9)

Задаем начальные приближения ,.

Запишем достаточное условие сходимости и определяем ,:

и

Определяем частные значения ,, которые удовлетворяют неравенствам

и

Переходим к реализации итерационного процесса:

Определяем погрешность по формуле :

Таким образом, имеем решение: ,.

Программа, реализующая решение данной задачи, представлена на рис. 3.1.

CLS

INPUT X,Y, M1,M2

1 X=X-(2*SIN(X+1)-Y - 0.5)/M1

Y=Y-(10*COS(Y-1)-X+0.4)/M2

PRINT X,Y

INPUT TT

GOTO 1

END

Рис. 3.1. Программа решения системы нелинейных уравнений методом Зейделя.