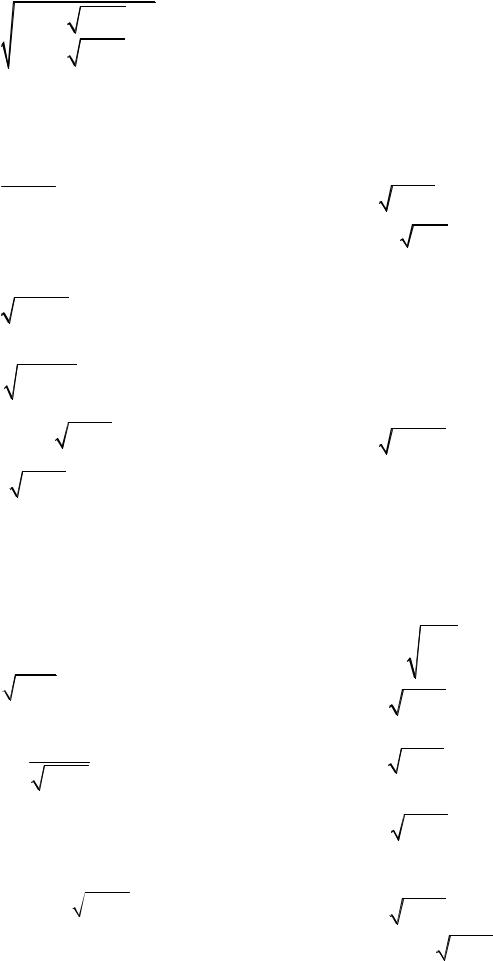
14.31. y = |
tg x + |
2tg x |
+1 |
. |
tg x - |
|
|
||
|
2tg x +1 |
|||
Задача 15. Найти производную y′x .
ïx = 3t2 +3 1,
ï3t
15.1.í
ïy = sinæ t3 + t ö.
ïç 3 ÷
î è øì
ìx = |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2t - t2 , |
|
|
|
|
|
|||||||||
ï |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
15.3. í |
y = |
|
|
|
|
|
|
|
|
|
. |
|
|
||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
|
(1- t)2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 |
+1), |
||||
ïx = ln(t + t |
|
|
|
||||||||||||
15.5. í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
t |
2 |
+1. |
|
|
|
|
|
|||
îy = t |
|
|
|
|
|
|
|
|
|||||||
ïx = ctg(2et ),
15.7.í
ïy = ln(tget ).
îì
ìx = arctget
2 ,
ï
15.9. í
ïîy =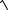 
et +1.
ïx = ln 1 ,
ï1- t4
15.11.í
ïïy = arcsin 1-+ t2 .
î 1 t2ì
ìïx = arcsin(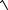
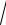1- t2 ),
15.13. í
ïîy = (arccost )2 .
ì |
|
|
|
|
|
|
|
- t |
2 |
, |
|
||
ïx = 1 |
|
|
||||
15.2. í |
|
|
|
|
|
|
ïy = tg |
|
1+ t |
. |
|||
î |
|
|
|
|
|
|
ìx = arcsin (sint ),
ï
15.4. í
ïîy = arccos(cost).
ì |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2t - t |
2 |
, |
|
|
|
||||||||||
ïx = |
|
|
|
|
|
|
|
||||||||||||
15.6. í |
y = arcsin (t -1). |
|
|||||||||||||||||
ï |
|
||||||||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ìx = ln(ctgt), |
|
|
|
||||||||||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15.8. í |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
ïy = |
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
t |
|
|
|
|
|
|
|
|
|||||||
î |
|
cos |
|
|
|
|
|
|
|
|
|
||||||||
ì |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1- t |
|
|
|
||||||||
ïx = ln |
|
|
|
|
|
|
|
|
, |
|
|||||||||
|
1+ t |
|
|||||||||||||||||
15.10. í |
|
|
|
|
|
|
|
|
|
|
|
||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1- t |
2 |
. |
|
|
|
||||||||||
îy = |
|
|
|
|
|
||||||||||||||
ìx = |
|
|
|
|
|
|
|
|
|
||||||||||
1- t2 , |
|
|
|
||||||||||||||||
ï |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
||
15.12. í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ïy = |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1- t2 |
|
|
|
|
|||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ì |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
ïx = |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ï |
|
|
|
|
1- t2 |
|
|
|
|
|
|
|
|||||||
15.14. í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ 1- t2 |
|
|||||||||||
ï |
|
|
|
|
|
|
|
. |
|||||||||||
ïy = ln |
|
|
|
|
|
|
t |
|
|
||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
51
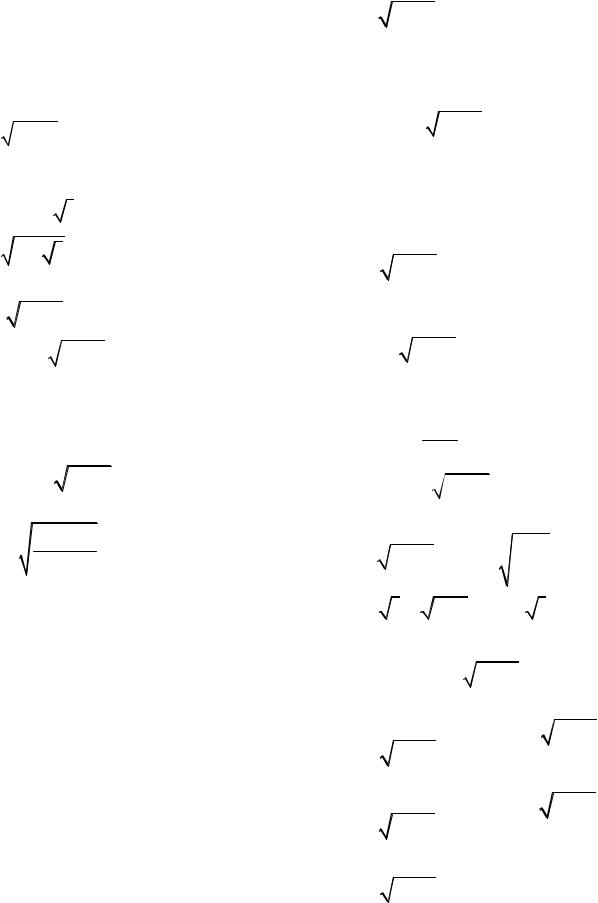
ìx = |
(1+ cos2 t )2 , |
ï |
|
15.15. í |
cost . |
ïy = |
|
î |
sin2 t |
ïx = arccos1t ,
15.17.í
ïïîy = 
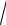t2 -1 + arcsin1t .ì
ì |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t , |
|
|
|
||
ïx = arcsin |
|
|
|
|
|
|
|
||||||
15.19. í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ïy = |
1+ |
t |
. |
|
|
|
|||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
ìx = t |
|
|
|
|
|
|
|
|
|
||||
|
|
|
t2 +1, |
|
|
|
|||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
15.21. í |
|
|
|
1+ |
1+ t |
2 |
|
|
|||||
ïy = ln |
|
. |
|||||||||||
|
t |
|
|||||||||||
î |
|
|
|
|
|
|
|
||||||
ïx = ln(1- t2 ),
15.23.í
ïy = arcsin 1- t2 .
îì
ì
ïx = ln
ï
15.25. í
ïïîy = 12 tg2 t + ln cost.
ìx = lntgt, |
|
|||
ï |
1 |
|
|
|
15.27. í |
|
|
||
ïy = |
|
|
|
. |
sin |
2 |
t |
||
î |
|
|
||
ìïx = esec2 t ,
15.29. í
ïîy = tgt ×lncost + tgt - t.
ì |
|
|
|
|
1- t |
|
|
|
|
|
|
|
|
|||||
ïx = ln |
|
|
|
|
|
|
, |
|
|
|
|
|||||||
1 |
+ t |
|
|
|
|
|||||||||||||
15.16. í |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1- t |
2 |
. |
|
|
|
|
|||||||||||
îy = |
|
|
|
|
|
|
|
|||||||||||
ì |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ïx = |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
lnt |
|
|
|
|
|
|
|
|
|
|
||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
15.18. í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ 1- t2 |
|||||||||||||
ï |
|
|
|
|
|
|||||||||||||
ïy = ln |
|
|
|
|
|
|
|
|
t |
. |
||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ìx = |
(arcsint )2 , |
|||||||||||||||||
ï |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
15.20. í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ïy = |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
î |
|
|
1- t2 |
|
|
|
|
|||||||||||
ìx = arctgt, |
|
|
|
|
|
|
|
|
||||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
15.22. í |
|
|
|
|
|
|
1+ t |
|
|
|
||||||||
ïy = ln |
|
|
|
. |
|
|||||||||||||
|
|
t +1 |
|
|
||||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
||||||||
ì |
|
|
|
|
|
|
|
t +1 |
||||||||||
ïx = arctg
15.24.í t -1
ïîy = arcsin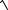 
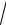1- t2 .,
ì |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1- t |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ïx = |
|
t - t2 - arctg |
, |
|
|
|||||||||||||||||||
|
|
t |
|
|
||||||||||||||||||||
15.26. í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t - |
1- t arcsin t. |
|
|
|||||||||||||||||
îy = |
|
|
|
|
||||||||||||||||||||
ì |
t |
2 |
|
lnt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ïx = |
|
|
|
|
+ ln 1- t2 , |
|
|
|
|
|
||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||
ï |
1- t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
15.58. í |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ïy = |
|
|
|
|
|
|
|
|
arcsint + ln |
|
1- t2 . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ï |
|
|
|
|
1- t |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ì |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
ïx = |
|
|
|
|
|
|
|
|
|
|
arcsint + ln |
|
1- t |
|
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ï |
|
|
|
1- t2 |
|
|
|
|
|
|||||||||||||||
15.30. í |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ïy = |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ï |
|
|
|
|
1- t |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
52
ïx = ln(t + 
15.31.í
ïy = 1+ t2 - ln 1+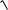 
1+ t2 .
ïî t1+ t2 ),ì
Задача 16. Составить уравнения касательной и нормали к кривой в точке соответствующей значению параметра t = t0 .
ì |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
ïx = asin |
t, |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
16.1. í |
|
|
|
|
|
|
t |
|
= π 3. |
|
|
||
ïy = a cos3 t, |
0 |
|
|
||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
ìx = a(t - sint), |
|
|
|
|
|
||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
16.3. í |
y = a(1- cost ), |
t |
|
= π 3. |
|||||||||
ï |
0 |
||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
ì |
|
2t + t2 |
|
|
|
|
|
|
|
||||
ïx = |
|
|
|
|
, |
|
|
|
|
|
|
|
|
1+ t |
3 |
|
|
|
|
|
|
|
|
||||
ï |
|
|
|
|
|
|
|
|
|
|
|
||
16.5. í |
|
2t - t |
2 |
|
|
|
|
|
|
|
|
||
ï |
|
|
t0 |
=1. |
|
|
|
||||||
ïy = |
1+ t |
3 |
, |
|
|
|
|||||||
î |
|
|
|
|
|
|
|
|
|
|
|
||
ìx = t (t cost - 2sint ), |
|
|
|||||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
16.7. í |
y = t (t sint + 2cost), t |
|
= π 4. |
||||||||||
ï |
0 |
||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
ìx = 2ln |
(ctgt) + ctgt, |
|
|
|
|||||||||||
16.9. í |
|
|
|
|
|
|
t0 = π 4. |
||||||||
îy = tgt |
+ ctgt, |
||||||||||||||
ìx = at cost, |
|
|
|
|
|
|
|
|
|
|
|
|
|||
16.11. í |
|
|
|
|
|
t0 |
= π 2. |
|
|||||||
îy = at sint, |
|
|
|
||||||||||||
ì |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
ïx = arcsin |
|
|
|
|
|
|
|
|
, |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
ï |
|
|
|
1+ t2 |
|
|
|
||||||||
16.13. í |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
ïy = arccos |
|
|
|
|
|
|
, |
t |
0 |
=1. |
|||||
|
|
|
|
|
|
|
|
|
|||||||
ï |
|
|
|
|
1+ t |
2 |
|
|
|
|
|
||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|||
ì |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 cost, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
ïx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
16.2. í |
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
= π 3. |
|
|
|||||||||||
ïy = sint, |
|
|
|
|
0 |
|
|
|
|
||||||||||||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ì |
|
|
|
|
|
|
|
|
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ïx = 2t - t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
16.4. í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1. |
|
|
|
|||||
ïy = 3t - t3 , t |
0 |
|
|
|
|||||||||||||||||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ì |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
ïx = arcsin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ t2 |
|
|
|
||||||||||||
16.6. í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
ïy = arccos |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
t |
0 |
= -1. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ t |
2 |
|
|
|
|
|
||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ì |
|
3at |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ïx = |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ t |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
16.8. í |
3at2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ïy = |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
t0 |
= 2. |
|
|
|
||||||||||||
1+ t |
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ìx = |
|
1 |
t2 |
- |
|
1 |
|
t4 |
, |
|
|
|
|
|
|
|
|
||||||||||||||
2 |
4 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
16.10. í |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ï |
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||||||||
ïy = |
|
|
|
|
t |
|
|
+ |
|
|
|
|
|
|
|
t |
|
, t0 = 0. |
|||||||||||||
2 |
|
|
|
3 |
|
||||||||||||||||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ìx = sint, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
16.12. í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
= π 6. |
|
|
|||||||||||
îy = cost, |
|
|
|
|
|
|
|||||||||||||||||||||||||
ìx = |
1+ lnt , |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
ï |
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
16.14. í |
|
|
3 + 2lnt |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
ï |
|
|
|
, |
|
t0 |
=1. |
|
|||||||||||||||||||||||
ïy = |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
53
ìx = 1+ t |
, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ï |
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
16.15. í |
|
|
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ïy = |
2t |
2 |
|
|
|
+ |
|
t |
|
, |
|
t0 = 2. |
|
|
|
||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ìx = a(t sint + cost ), |
|
|
|
||||||||||||||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16.17. í |
y = a(sint - t cost ), |
t |
|
= π 4. |
|||||||||||||||||||
ï |
0 |
||||||||||||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì |
|
|
|
- t |
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
||||||
ïx =1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
16.19. í |
|
|
|
- t |
3, t |
|
= 2. |
|
|
|
|||||||||||||
ïy = t |
0 |
|
|
|
|||||||||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ìx = t |
(1- sint ), |
|
|
|
|
|
|||||||||||||||||
16.21. í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
|
|
|
|
|
|
|
îy = t cost, |
|
|
= 0. |
|
|
|
|||||||||||||||||
ìx = 3cost, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
16.23. í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
= π 4. |
|
|
|||
îy = 4sint, |
|
|
|
|
|
||||||||||||||||||
ì |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ïx = t |
+1, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
16.25. í |
|
|
|
2 + t +1, t |
|
=1. |
|
|
|
||||||||||||||
ïy = t |
0 |
|
|
|
|||||||||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ìx = 2tgt, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
16.27. í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
= π 4. |
|
îy = 2sin2 t + sin 2t, |
|||||||||||||||||||||||
ìx = sint, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
16.29. í |
|
|
|
|
|
|
|
|
|
|
|
t0 |
|
|
|
|
|
|
|
|
|
||
îy = at , |
|
|
|
|
= 0. |
|
|
|
|
|
|||||||||||||
ì |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ïx = 2e |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
16.31. í |
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
= 0. |
|
|
|
|
|||
ïy = e−t , |
|
|
|
0 |
|
|
|
|
|
||||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
ïx = asin |
|
t, |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
16.16. í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
= π 6. |
||
ïy = a cos3 t, |
|
0 |
|||||||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ìx = t +1 |
, |
|
|
|
|
|
|
|
|
|
|||||||||
ï |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16.18. í |
t -1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
||||||||
ïy = |
|
|
|
|
|
|
|
|
, |
|
|
t0 = -1. |
|||||||
|
|
|
t |
|
|
|
|
||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ì |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
), |
|
|
|
|
|
ïx = ln(1+ t |
|
|
|
|
|
||||||||||||||
16.20. í |
|
|
- arctgt, |
|
t |
|
=1. |
||||||||||||
ïy = t |
|
0 |
|||||||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì |
12+ t |
3 |
|
, |
|
|
|
|
|
|
|
||||||||
ïx = |
|
|
|
|
|
|
|
|
|||||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
t |
|
|
-1 |
|
|
|
|
|
|
|
|
|
|||||||
16.22. í |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ïy = |
|
|
|
|
|
|
|
|
|
|
, |
|
t0 |
= 2. |
|||||
t |
2 |
-1 |
|
||||||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|||||||||
ì |
|
|
- t |
4 |
, |
|
|
|
|
|
|
|
|||||||
ïx = t |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
16.24. í |
|
|
2 - t3 , t |
|
=1. |
||||||||||||||
ïy = t |
0 |
||||||||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ìx = 2cost, |
|
|
|
|
|
|
|
||||||||||||
16.26. í |
|
|
|
|
|
|
|
|
|
|
|
|
t0 = -π 3. |
||||||
îy = sint, |
|
|
|
||||||||||||||||
ì |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ïx = t |
|
+1, |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
16.28. í |
|
|
2 , |
|
|
|
|
t |
|
= -2. |
|
|
|||||||
ïy = t |
|
|
|
|
0 |
|
|
||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ìx = sint, |
|
|
|
|
|
|
|
|
|
|
|||||||||
16.30. í |
|
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
= π 6. |
||||
îy = cos2t, |
|
||||||||||||||||||
Задача 17. Найти производную n -го порядка.
17.1. y = xeax . 17.2. y = sin 2x + cos(x +1).
54