Задача 3. Найти общий интеграл дифференциального уравнения.

Задача 3. Найти общий интеграл дифференциального уравнения.

Задача 5. Решить задачу Коши.

Задача 4. Найти решение задачи Коши.

Задача 5. Решить задачу Коши.

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный университет информатики и радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

TR_Kuvnecov.pdf

Скачиваний:

Добавлен:

11.05.2015

Размер:

1.61 Mб

Скачать

☆

<<< < Предыдущая 8 9 10 11 12 13 14 15 16 17 18 1920 / 4320 21 22 23 24 25 26 27 28 29 30 31 32 > Следующая >>>

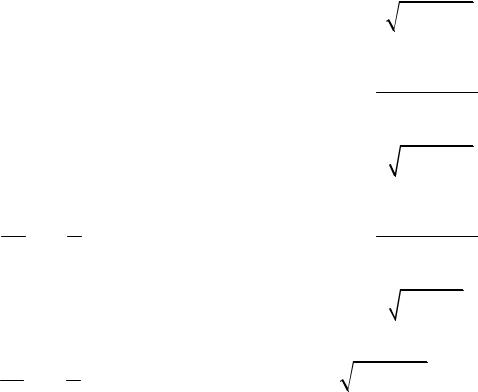
2.19. y	′	=	x2 + 3xy − y2
						.
			3x2 − 2xy
	′		y2		y
2.21. y		= x2		+ 8 x +12.

2.23. y	′	=	x2	+ xy − 3y2
						.
				x2 − 4xy

2.25. 4y′ = y2 +10 y + 5.

x2 x

2.27. y	′	=	x2 + xy − 5y2
				.
			x2 − 6xy

2.29. 3y′ = y2 +10 y +10. x2 x

2.31. y	′	=	x2	+ 2xy − 5y2
				2x2 − 6xy .

2.20. xy′ = 3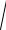2x2 + y2 + y.

′ = 3y3 +12yx2

2.22. xy 2y2 + 6x2 .

2.24. xy′ = 23x2 + y2 + y.

′ = 3y3 +14yx2

2.26. xy 2y2 + 7x2 .

2.28.xy′ = 4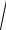x2 + y2 + y.

2.30.xy′ = 4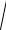2x2 + y2 + y.

3.1. y	′	=		x + 2y − 3
					2x − 2 .

3.3. y	′	=		3y − x − 4					.
					3x + 3
3.5. y′		=		x + y − 2
								.
				3x − y − 2
3.7. y′		=		x + y − 8
							.
				3x − y − 8
3.9. y′		=			3y + 3
						.
				2x + y −1
		′			x − 2y + 3

3.11. y			= −2x − 2 .


3.2. y	′	=	x + y − 2
				2x − 2 .

	′			2y − 2
3.4. y		= x + y − 2.

3.6. y′ =			2x + y − 3		.

				x −1
3.8. y	′	=	x + 3y + 4
				3x − 6 .

3.10. y′ =				x + 2y − 3
						.
				4x − y − 3

3.12. y′ =	x + 8y − 9
		.
	10x − y − 9

110

3.13. y¢ = 2x + 3y − 5.

5x - 5

¢= x + 3y − 4

3.15.y 5x - y - 4 .

3.17.y¢ = x + 2y − 3.

x-1

3.19. y¢ =			5y + 5			.
			4x + 3y -1
3.21. y	¢	=	x + y + 2	.
			x +1
3.23. y	¢	=	2x + y − 3		.
			2x - 2

¢= x + 5y − 6

3.25.y 7x - y - 6.

3.27. y	¢	=	2x + y −1	.
			2x - 2
3.29. y¢ =			6y − 6			.
			5x + 4y - 9
3.31. y¢ =			y + 2		.
			2x + y - 4

3.14. y¢ =	4y − 8
		.
	3x + 2y - 7

3.16.y¢ = y − 2x + 3.

x-1

3.18.y¢ = 3x + 2y −1.

x+1

¢= x + 4y − 5

3.20.y 6x - y - 5.

3.22. y

2x + y − 3

4x - 4

3.24. y¢ =

2x + 2y - 2

3.26. y

x + y − 4

x - 2

3.28. y

3y − 2x +1

3x + 3

¢= x + 6y − 7

3.30.y 8x - y - 7 .

	Задача 4. Найти решение задачи Коши.
4.1. y¢ - y x = x2 , y(1) = 0.					4.2. y′ - y ctg x = 2xsin x, y(π 2) = 0.
	¢		1		¢	2
4.3. y		+ y cos x = 2 sin 2x, y(0) = 0. 4.4.		y		+ y tg x = cos x, y(π 4) =1 2.

4.5. y¢ -		y	= x	2	+ 2x,		y(-1) = 3 2.4.6. y¢ -
	x + 2
4.7. y¢ -	y				æπ		ö		4.8. y¢ +
		= xsin x, yç					÷	=1.
	x					2
					è		ø

	1	y = ex (x +1),		y(0) =1.
x +1		y = ex (x +1),		y(0) =1.
x +1
y	= sin x,		y(π ) =	1	.
x	= sin x,		y(π ) =		.
x				π

111

4.9. y′ +

= x

y(1) =1.

4.11. y

′

−

2x − 5

= 5,

y(2) = 4.

4.13. y′

−

= −2

ln x

y(1) =1.

4.15. y′

y(1) = −5 6.

y = x

4.17. y′

−

2xy

1+ x

, y(1) = 3.

1+ x2

4.19. y

′

y(1) =1.

4.10. y′ +

y =

2x2

y(0) =

1+ x2

4.12. y′ +

x +1

, y(1) = e.

4.14. y′ −

y(1) = 4.

= −

4.16. y′ +

= 3x,

y(1) =1.

4.18. y

′

1− 2x

y =1,

y(1) =1.

4.20. y′ + 2xy = −2x3 ,

y(1) = e−1 .


4.21. y′ +		xy					x		(0) =		2
				=				, y			3.
		2(1− x2 )				2
4.23. y′ −		2	y = e		x	(x +1)			2	, y	(0) =1.
	x +1

4.25. y′ − 2y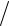(x +1) = (x +1)3 , y(0) =1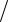2.

4.27.	y′ − 4xy = −4x3 ,	y(0) = −1 2.
4.29.	y′ − 3x2 y = x2 (1+ x3 ) 3,		y(0) = 0.
4.31.	y′ − y x = −2 x2 ,	y(1)	=1.

4.22. y′ + xy = −x3 ,					y(0) = 3.
4.24. y′ + 2xy = xe−x2 sin x,						y(0) =1.
4.26. y′ − y cos x = −sin 2x,						y(0) = 3.
4.28. y′ −	y		ln x
		= −		,	y(1)	=1.
	x		x
4.30. y′ − y cos x = sin 2x,						y(0) = −1.

5.3.	y2dx + (xy −1)dy = 0,	y

5.4.	2(4y2 + 4y − x) y′ =1,	y

x=1

x=0

=e.

=0.

112

5.5. (cos2y cos2 y - x) y¢ = sin y cos y,

x=1 4

= π 3.

5.6. (xcos2 y - y2 ) y¢ = y cos2 y,

x=π

= π 4.

5.7. ey2 (dx - 2xydy) = ydy,

x=0

= 0.

5.8. (104y3 − x) y′ = 4y,

x=8 = 1.

5.9. dx + (xy - y3 )dy = 0,

x=−1

= 0.

5.10. (3y cos2y - 2y2 sin 2y - 2x) y¢ = y,

x=16

= π 4.

5.11. 8(4y3 + xy - y)y¢ =1,

x=0

= 0.

5.12. (2ln y - ln2 y)dy = ydx - xdy,

x=4

= e2 .

5.13. 2(x + y4 ) y¢ = y, y

x=−2

= -1.

5.14. y3 ( y -1)dx + 3xy2 ( y -1)dy = ( y + 2)dy,

x=1 4

= 2.

5.15. 2y2dx + (x + e1 y )dy = 0,

x=e

=1.

5.16. (xy +

)dy + y2dx = 0,

x=−1 2

= 4.

5.17. sin 2ydx = (sin2 2y - 2sin2 y + 2x)dy,

x=−1 2

= π 4.

5.18. (y2 + 2y - x) y¢ =1,

x=2

= 0.

=1.

5.19. 2y

x=−4

ydx − (6x y + 7)dy = 0,

5.20. dx = (sin y + 3cos y + 3x)dy,

x=eπ 2

= π 2.

5.21. 2(cos2 y ×cos2y - x) y¢ = sin 2y,

x=3 2

= 5π 4.

5.22. ch ydx = (1+ xsh x)dy,

x=1 = ln 2.

5.23. (13y3 - x)y¢ = 4y,

x=5

=1.

5.24. y2 (y2 + 4)dx + 2xy(y2 + 4)dy = 2dy,

x=π

= 2.

5.25. (x + ln2 y - ln y) y¢ = y 2,

x=2

=1.

113

<<< < Предыдущая 8 9 10 11 12 13 14 15 16 17 18 1920 / 4320 21 22 23 24 25 26 27 28 29 30 31 32 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.03.2025384.51 Кб0trebovania_k_oformleniyu.doc
#
01.05.2025355.84 Кб0Trebovanie_k_oformleniyu_otcheta_po_praktike_iz...doc
#
11.05.20152.68 Mб15Trifonov_Analit_geom.pdf
#
01.05.2025519.78 Кб0TRPO_otvety.docx
#
07.11.2018624.34 Кб10TRPO_конспект_3_курс.docx
#
11.05.20151.61 Mб23TR_Kuvnecov.pdf
#
11.05.2015808.24 Кб5tt.pdf
#
11.05.20151.24 Mб4turing.pdf
#
11.05.2015481.8 Кб41TV(digital).pdf
#
04.12.2018327.17 Кб9TYeHNIKA_RYeChI.doc
#
01.05.20252.89 Mб0T_1A_1.doc

5.1. y2dx + (x + e2 y )dy = 0,

5.1. y2dx + (x + e2 y )dy = 0,

5.2. (y4 ey + 2x) y′ = y, y