Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный университет информатики и радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

TR_Kuvnecov.pdf

Скачиваний:

Добавлен:

11.05.2015

Размер:

1.61 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 4310 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

3.13. y =

(-x2 + 7x - 7)

[1, 4].

x2 - 2x + 2

[1, 5].

3.15. y = 3

2(x − 2)2 (5 − x)

3.17. y = -

+ 8,

[-4,

-1].

3.19. y =

-2x(2x + 3)

[1, 4].

x2 + 4x + 5

[0,

4].

3.21. y = 3

2(x −1)2 (x − 4)

3.23. y = 2

− x + 2,

[1, 5].

x −1

3.25. y = -

+ 2x +

+ 5, [-2, 1].

+ 3,

[−4, 2].

3.27. y = 3

2(x + 2)2 (x − 4)

3.29. y =

- 8x -15,

ê-2, -

ú.

3.31. y = -

10x +10

[-1, 2].

x2 + 2x + 2

3.14. y = x − 4

+ 8,

[−1, 7].

x + 2

3.16. y =

[-4, 2].

+ x2

3.18. y = 3

[-2, 4].

2x2 (x - 6)

3.20. y = -

2(x2 + 3)

[-5, 1].

x2 + 2x + 5

3.22. y = x2 - 2x +

-13,

[2, 5].

x -1

[−3, 4].

3.24. y = 3

2(x + 2)2 (1− x)

3.26. y = 8x +

-15,

, 2ú.

3.28. y = x2 + 4x +

- 9,

[-1, 2].

x + 2

[−2, 5].

3.30. y = 3

2(x +1)2 (x − 2)

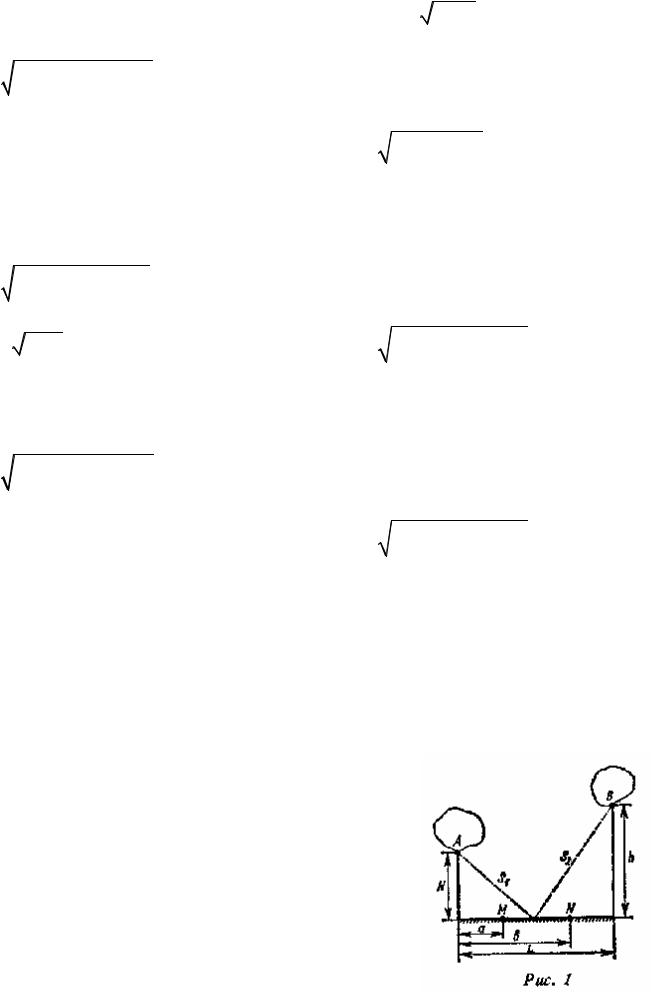
Задача 4.

Варианты 1 – 10. Рыбаку нужно переправиться с острова A на остров

B (рис. 1). Чтобы пополнить свои запасы, он должен попасть на участок берега MN . Найти кратчайший путь

рыбака s = s1 + s2 .
4.1. a = 200,	b = 300,	H = 400,	h = 300,	L = 700.
4.2. a = 400,	b = 600,	H = 800,	h = 600,	L = 1400.


4.3. a = 600,	b = 900,	H = 1200,		h = 900,		L = 2100.
4.4. a = 800,	b = 1200,	H = 1600,		h = 1200,			L = 2800.
4.5. a = 1000,	b = 1500,		H = 2000,		h = 1500,		L = 3500.
4.6. a = 400,	b = 500,	H = 300,		h = 400,		L = 700.
4.7. a = 800,	b =1000,	H = 600,		h = 800,		L = 1400.
4.8. a = 1200,	b = 1500,		H = 900,	h = 1200,			L = 2100.
4.9. a = 1600,	b = 2000,		H =1200,		h = 1600,		L = 2800.
4.10. a = 2000, b = 2500,			H = 1500,		h = 2000, L = 3500.
			Варианты 11 – 20.

При подготовке к экзамену студент за t дней изучает t + k -ю часть курса, а забывает

αt -ю часть. Сколько дней нужно затратить на подготовку, чтобы была изучена максимальная часть курса?

4.11. k = 1	2	,	α =			2	49		.		4.12. k = 1	2	,	α =		2 .
	2						49					2					81
4.13. k = 1	2	,	α =			2 .					4.14. k = 1	2	,	α =		2	169			.
	2						121					2					169
4.15. k =1,		α =		1	25			.			4.16. k =1,		α = 1 .
					25									16
4.17. k =1,		α =		1	36			.			4.18. k =1,		α = 1		49			.
					36										49
4.19. k = 2,		α = 1 .									4.20. k = 2,			α = 2		49			.
					18											49
											Варианты 21 – 31.
Тело массой						m0 = 3000 кг					падает с высоты H			м и теряет массу (сгорает
пропорционально				времени						падения. Коэффициент пропорциональности											k =100 кг/с2
Считая, что			начальная							скорость	v = 0, ускорение		g = 10					м/с2,			и пренебрега
											0
сопротивлением воздуха найти наибольшую кинетическую энергию тела.
4.21. H = 500.										4.22. H = 605.									4.23. H = 720.
4.24. H = 845.										4.25. H = 980.									4.26. H =1125.
4.27. H =1280.										4.28. H =1445.									4.29. H =1620.
4.30. H =1805.										4.31. H = 2000.

Задача 5. Исследовать поведение функций в окрестностях заданных точек помощью производных высших порядков.

5.1. y = x2 − 4x − (x − 2)ln(x −1)					,		x	= 2.
							0
5.2. y = 4x − x2 − 2cos(x − 2),				x = 2.
					0
5.3. y = 6ex−2 − x3 + 3x2 − 6x,				x	= 2.
				0
5.4. y = 2ln (x +1) − 2x + x2 +1,					x		= 0.
						0
5.5. y = 2x − x2 − 2cos(x −1),				x		=1.
				0
5.6. y = cos2 (x +1) + x2 + 2x,				x	= −1.
				0
5.7. y = 2ln x + x2 − 4x + 3,			x	=1.
			0
5.8. y =1− 2x − x2 − 2cos(x +1),						x = −1.
							0
5.9. y = x2 + 6x + 8 − 2ex+2 ,			x	= −2.
			0
5.10. y = 4x + x2 − 2ex+1,	x		= −1.
	0
5.11. y = (x +1)sin(x +1) − 2x − x2 ,							x		= −1.
							0
5.12. y = 6ex−1 − 3x − x3,	x	=1.
	0
5.13. y = 2x + x2 − (x +1)ln(		2 + x),					x		= −1.
							0
5.14. y = sin2 (x +1) − 2x − x2 ,				x		= −1.
				0
5.15. y = x2 + 4x + cos2 (x + 2),					x		= −2.
					0
5.16. y = x2 + 2ln (x + 2),	x = −1.
		0
5.17. y = 4x − x2 + (x − 2)sin(x − 2),								x = 2.
								0
5.18. y = 6ex − x3 − 3x2 − 6x − 5,					x		= 0.
						0
5.19. y = x2 − 2x − 2ex−2 ,	x		= 2.
	0
5.20. y = sin2 (x + 2) − x2 − 4x − 4,							x	= −2.
							0
									67

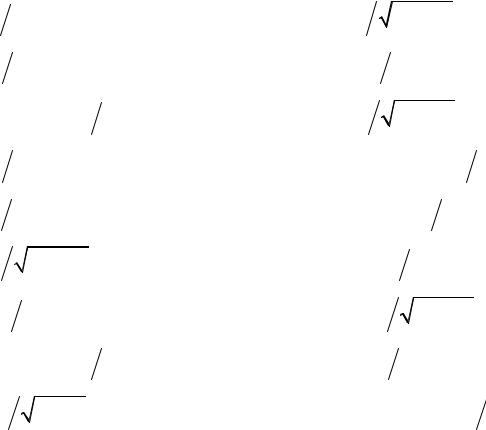
5.21. y = cos2 (x −1) + x2 − 2x,	x =1.
	0
5.22. y = x2 − 2x − (x −1)ln x,	x =1.
	0
5.23. y = (x −1)sin(x −1) + 2x − x2 ,		x = 1.
		0
5.24. y = x2 − 4x + cos2 (x − 2),	x	= 2.
	0

5.25. y = x4 + 4x3 +12x2 + 24(x +1− ex ), x = 0.
					0
5.26. y = sin2 (x − 2) − x2 + 4x − 4,				x	= 2.
				0
5.27. y = 6ex+1− x3 − 6x2 −15x −16,				x	= −1.
				0
5.28. y = sin x + sh x − 2x,		x0	= 0.
5.29. y = sin2 (x −1) − x2 + 2x,			x =1.
			0
5.30. y = cos x + ch x,	x0	= 0.
5.31. y = x2 − 2ex−1,	x =1.
	0

Задача 6. Найти асимптоты и построить графики функций.

6.1. y = (17 − x2 )

(4x − 5).

6.2. y = (x2 +1)

4x2 − 3.

6.3. y = (x3 − 4x)

(3x2 − 4).

6.4. y = (4x2 + 9)

(4x + 8).

6.5. y = (4x3 + 3x2 − 8x − 2)

(2 − 3x2 ).

6.6. y = (x2 − 3)

3x2 − 2

6.7. y = (2x2 − 6)

(x − 2).

6.8. y = (2x3 + 2x2 − 3x −1)

(2 − 4x2 ).

6.9. y = (x3 − 5x)

(5 − 3x2 ).

6.10. y = (2x2

− 6x + 4) (3x − 2).

6.11. y = (2 − x2 )

6.12. y = (4x3

− 3x)

(4x2 −1).

9x2 − 4

6.13. y = (3x2 − 7)

(2x +1).

6.14. y = (x2 +16)

9x2 − 8

6.15. y = (x3 + 3x2 − 2x − 2)

(2 − 3x2 ).

6.16. y = (21− x2 )

(

7x + 9).

6.17. y = (2x2 −1)

6.18. y = (2x3

− 3x2 − 2x +1)

(1− 3x2 ).

x2 − 2

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 4310 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.03.2025384.51 Кб0trebovania_k_oformleniyu.doc
#
01.05.2025355.84 Кб0Trebovanie_k_oformleniyu_otcheta_po_praktike_iz...doc
#
11.05.20152.68 Mб15Trifonov_Analit_geom.pdf
#
01.05.2025519.78 Кб0TRPO_otvety.docx
#
07.11.2018624.34 Кб10TRPO_конспект_3_курс.docx
#
11.05.20151.61 Mб23TR_Kuvnecov.pdf
#
11.05.2015808.24 Кб5tt.pdf
#
11.05.20151.24 Mб4turing.pdf
#
11.05.2015481.8 Кб41TV(digital).pdf
#
04.12.2018327.17 Кб9TYeHNIKA_RYeChI.doc
#
01.05.20252.89 Mб0T_1A_1.doc