Гл.II. Квантовая электродинамика (кэд)10.10.02
Квантовая электродинамика (КЭД) – это наука о взамодействии фотонов и точечных частиц со спином 1/2. Ее можно использовать для количественных предсказаний только в тех случаях, когда другими взаимодействиями, формирующими конечные размеры частиц можно пренебречь. Фактически это означает, что КЭД описывает только превращения частиц , не участвующих в сильном взаимодействии,т.е. взаимопревращения заряженных лептонов и фотонов.
Это, однако, не значит, что КЭД является бесполезной наукой, когда речь идет о взаимодействии электронов и адронов. Напротив, КЭД и в этих ситуациях играет очень важную роль, как, например, в глубоко-неупругих процессах с адронами (см. гл.IV), давая базисную формулу с правильной параметризацией рассеяния электронов на кварке.
§1. Амплитудное описание процессов.
§2. Квантово-электродинамические процессы: эффект Комптона и явление аннигиляции.
1. В этом параграфе мы более или менее детально проанализируем два процесса - неупругое рассеяние фотона на электроне и аннигиляцию электрона с позитроном. Метод анализа с позиций "здравого смысла" и основные результаты будут использоваться в дальнейшем при анализе других процессов в стандартной модели.
В первом неисчезающем приближении рассеяние фотонов на свободных электронах - эффект Комптона - представляется двумя фейнмановскими диаграммами:
(2.1)
Первая из них соответствует следующей последовательности процессов: электрон поглощает фотон, распространяется как виртуальный электрон и затем распадается на реальные электрон и фотон. Вторая (правая) диаграмма (2.1) соответствует испусканию конечного фотона начальным электроном с последующим поглощением начального фотона виртуальным электроном с превращением его в физический электрон.
2. Рассмотрим сначала кинематику Комптон-эффекта. Сохранение суммарного четыре-импульса означает, что
(k+p) = (k+p). (2.2)
Возводя в квадрат правую и левую части, получаем следующую цепочку равенств:
p2=(k–k+p)2,
m2=k2+k2+p2–2kk+2p(k–k), (2.3)
2p(k–k)=(k–k)2= –2kk.
В системе покоя начального электрона имеем:
m(cos, (2.4)
где - угол между направлениями k и k'.
Из (2.4) окончательно получаем:
.
(2.5)
Формула (2.5) связывает между собой частоты начального () и конечного () фотона с углом вылета рассеянного фотона. Обсудим коротко два предельных случая:
« m (2.6)
и
» m. (2.7)
При
«
m
0
и
,
т.е. фотон рассеивается практически
упруго.
Если » m, то соотношение между и зависит от угла . При малых углах , т.е. при углах
,
(2.8)
при которых
(2.9)
по порядку величины совпадает с . При больших углах, когда
,
(2.10)
должно быть
m. (2.11)
3. Перейдем теперь к оценке масштабов эффективного сечения рассеяния фотона на электроне. Рассмотрим отдельно нерелятивистский ( « m) и релятивистский ( » m) случаи. Сначала - нерелятивистский.
Как мы знаем (см. Приложение к главе I), эффективное сечение имеет размерность квадрата длины. Поэтому прежде всего нам нужно понять механизм возникновения величины с размерностью длины. В КЭД, казалось бы, таких величин и нет: фотоны и электроны являются точечными объектами, константа связи является безразмерной. Размерность длины возникает для Комптон-эффекта как радиус области взаимодействия электрона с фотоном, который в свою очередь определяется механизмом процесса. Для определенности будем иметь в виду левую диаграмму (2.1). Виртуальная частица, возникающая при поглощении начального фотона электроном, обладает энергией ( + m), которая отличается от энергии физического электрона на величину
.
(2.12)
Соответственно, время существования такой частицы имеет порядок
t 1/E, (2.13)
а проходимое ею расстояние
r=vt=t(k/m)=(/m)(1/E)=(/m)(1/)=1/m. (2.14)
Таким образом, механизм рассеяния фотона определяет радиус 1/m области взаимодействия. Поэтому сразу же хочется сделать вывод о том, что масштабы сечения должны иметь порядок
(1/m)2. (2.15)
В действительности это не совсем так. Мы уже указывали ранее (см. Гл. I), что далеко не каждый фотон, пролетающий сквозь область взаимодействия, вызывает реакцию: это делает в среднем один фотон из 1/ фотонов. Поэтому истинный масштаб сечения будет:
,
(2.16)
где
r0 =/m=2.810–13см (2.17)
есть классический радиус электрона.
4. Выясним теперь, как меняются масштабы сечения в релятивистской области » m. Для удобства рассуждений перейдем в систему центра масс фотона и электрона. В этой системе суммарный импульс Р фотона и электрона равняется нулю, а суммарная энергия, которая является в то же время энергией виртуальной частицы (электрона), будет значительно больше массы электрона. Отсюда следует, что из теории исчезает единственная размерная величина - масса электрона, и возникает вопрос, как же получить величину с размерностью см2?
Полное сечение с, которое мы обсуждаем, может зависить только от полной инвариантной массы (т.е. полной энергии в систеие центра инерции) w сталкивающихся фотона и электрона
w2 = s = (p+k)2. (2.18)
Поэтому должно быть
.
(2.19)
5. Теперь мы можем привести точные формулы для сечения Комптон-эффекта, даваемые КЭД. В лабораторной системе дифференциальное сечение имеет вид:
.
(2.20)
В пределе « m (нерелятивизм)
,
(2.21)
.
(2.21a)
Как и должно быть, мы получаем классическое томсоновское рассеяние фотонов свободными зарядами. Отметим, что сечение (2.21) не зависит от спина рассеивающей частицы.
Полное сечение рассеяния фотона на электроне дается формулой:
,
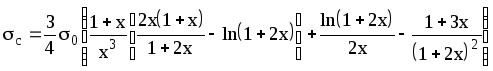(2.22)
где
,
x=/m.
В области « m эта формула превращается в (2.34), в области » m
.
(2.23)
Поучительно
проследить за тем, как получается
результат (2.23) в релятивистском случае
»
m. В области малых углов
и dc/d
~
r02.
Однако суммарный вклад этой области в
сечение дается формулой
.
При получении этой формулы мы воспользовались тем, что суммарный телесный угол при 0 равняется
.
(2.24)
Вклад больших углов также обращается в нуль, поскольку в этом случае m и
.
(2.25)
6. Проанализируем теперь явление аннигиляции ("исчезновения") электрона и позитрона. Оно состоит в превращении электрона и позитрона в фотоны и может происходить как в связанном состоянии электрона с позитроном (т.е. в позитронии Ps), так и при их столкновении ("на лету"). Рассмотрим сначала аннигиляцию на лету и будем считать, что налетающий позитрон обладает нерелятивистской энергией. Согласно КЭД, простейший процесс аннигиляции описывается диаграммой
(2.26)
Легко убедиться, однако, что однофотонная аннигиляция (2.26) запрещена законом сохранения энергии-импульса и, следовательно, может реализовываться только как виртуальный процесс. Допустимым механизмом аннигиляции является двухфотонная аннигиляция, описываемая диаграммой Фейнмана
(2.27)
На принятом здесь уровне "здравого смысла" эта означает следующее: налетающий электрон (то же справедливо и для позитрона, диаграмма Фейнмана описывает эти процессы одновременно) испускает физический фотон и виртуальный электрон, который аннигилирует с позитроном. По сказанному ранее (см. Гл. I, §2), виртуальный электрон в нерелятивистской области может “жить” только в течении времени 1/m. Поэтому рассматриваемый механизм аннигиляции предполагает "площадь" взаимодействия, по порядку величины равную (1/m)2, а с учетом константы взаимодействия площадь r02, где r0=/m является классическим радиусом электрона. Соответственно, масштаб эффективного сечения должен иметь порядок
~r02. (2.28)
Точный результат имеет вид
,
(2.29)
где v - скорость налетающего позитрона (электроны предполагаются покоящимися). Поучительно коротко обсудить соотношение формул (2.28) и (2.29). Множители и v имеют очевидное происхождение: r02 - площадь круга, v возникает из определения сечения (cм. Приложение II к Гл. I). Мы видим, таким образом, что масштаб r02 имеет существенно квантовомеханическое происхождение и связан с нетривиально возникающей вероятностью процесса. Множитель же v является "внешним", не следующим из квантовой теории и возникает как результат определения эффективного сечения. Тем не менее, множитель v в (2.29) играет важную практическую роль в экзотермических реакциях (т.е. реакциях, протекающих с выделением энергии). Он приводит к хорошо известному закону 1/v для эффективного сечения, который имеет очень большое значение в делении ядер медленными нейтронами.
7. Формула (2.42) относится к случаю, когда относительная скорость электрона и позитрона является нерелятивистской. В релятивистском случае, т.е. в случае, когда энергия Е налетающего позитрона
E » m (2.30)
эффективное сечение обращается в нуль, хотя область взаимодействия по-прежнему имеет порядок 1/m. Чтобы увидеть это, перейдем для удобства рассуждений в систему центра инерции сталкивающихся электрона и позитрона. Пусть р - импульс электрона и k - импульс фотона. В ситуации (2.30) эти импульсы должны быть по модулю примерно равны. Поэтому импульс виртуального электрона будет равняться:
pв=p – k 2p sin/2. (2.31)
где - угол вылета фотона. В области pв» m, т.е. в области больших углов вылета фотона, масса электрона исчезает как физический параметр и дифференциальное сечение аннигиляции должно быть обратно пропорционально p2 (другого размерного параметра просто нет!):
.
(2.32)
Таким образом, в области высоких энергий большие углы вносят исчезающе малый вклад в сечение аннигиляции.
В области малых углов p<m, т.е.
<m/p, (2.33)
проинтегрированное по углам сечение имеет порядок
,
(2.34)
где
- дифференциальное сечение под нулевым
углом вылета фотона, 1/2(m/p)2
есть телесный угол "малых углов":
.
(2.35)
Таким образом,
поведение сечения аннигиляции в области
больших энергий сталкивающихся электрона
и позитрона зависит от поведения
.
Если, например,
const,
(2.36)
то 0, если
,
(2.37)
то поведение полного сечения будет определяться типом бесконечности в (2.37).
8. Конечно, решить
вопрос о том, как будет вести себя
при высоких энергиях, можно только
располагая теорией - в данном случае
КЭД. Мы получим результат (2.36), используя
пару легко принимаемых гипотез типа
здравого смысла.
Как известно, в нерелятивистской квантовой теории амплитуда F упругого рассеяния бесспиновых частиц, взаимодействующих через потенциал V(r), имеет в борновском приближении вид:
,
(2.38)
где q=p–p, p, p - импульсы до и после столкновения, - приведенная масса.
В релятивистской области эта формула для амплитуды рассеяния F будет отличаться только в одном отношении: приведенная масса должна быть заменена на приведенную энергию:
,
(2.39)
где 1,2 - энергии сталкивающихся частиц.
Соответственно,
дифференциальное сечение
для бесспиновых частиц ведет себя
следующим образом:
.
(2.40)
Если рассеиваются частицы со спином, то в формулу (2.40) неодходимо добавить спиновые функции , поскольку в этом случае волновая функция частицы с импульсом р и проекцией спина m имеет вид:
pm = meipr. (2.41)
В релятивистской квантовой теории вопрос о спиновых функциях является достаточно сложным, но спиновые функции частиц со спином J=1/2 и безмассовых частиц со спином J=1 не вносят существенных энергетических множителей в амплитуду. Поэтому качественно формула (2.40) cохранится и в случае частиц со спином. Безмассовые фотоны вносят, однако, дополнительные факторы, учет которых превращает асимптотику (2.40) в (2.36). Действительно, как известно, фотоны входят в квантовую теорию через векторный потенциал А и роль волновой функции фотона играет потенциал
Ak ~ eeikr, (2.42)
где k - импульс фотона, e - его поляризация.
Однако нормировка этой волновой функции является необычной. Именно, чтобы получить энергию (один фотон!) в единице объема необходимо использовать потенциал
.
(2.43)
В этом легко убедиться, если вспомнить, что энергия Е электромагнитного (фотонного) поля дается формулой:
.
(2.44)
При нормировке (2.43) в (2.44) мы получаем Е=. Отсюда следует, что формулу (2.40) нужно умножить на (1/2)n, где n - число участвующих в реакции фотонов. В нашем случае n=2 и
const,
где мы положили p.
Таким образом, для сечения аннигиляции при больших энергиях получаем:
,
(2.45)
т.е. что сечение аннигиляции асимптотически обращается в ноль.
Теперь мы можем привести точную квантово-электродинамическую формулу для сечения аннигиляции (в л.с.):
,
(2.46)
где x=+/m и + - энергия налетающего позитрона.
В области (+ – m) « m = r02/v+, в области (+ – m) » m
.
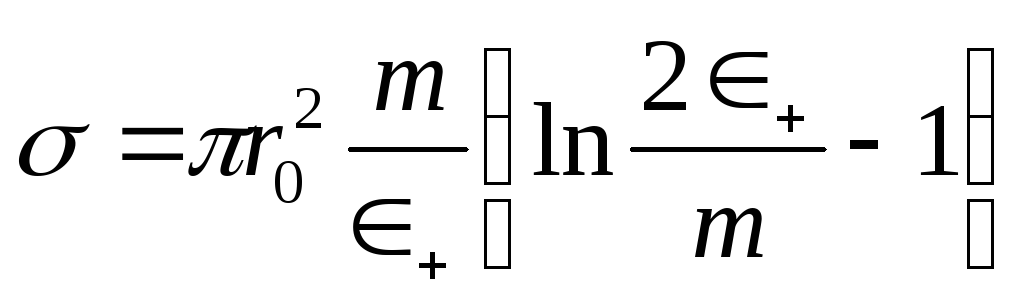(2.46)
10. Проанализируем теперь аннигиляцию остановившихся позитронов.В этом случае с большой вероятностью образуется позитроний Ps - водородо-подобный атом электрона и позитрона и необходимо рассматривать аннигиляцию связанных электрона и позитрона. Аннигиляция на лету является, как правило, двухфотонной - вероятность трехфотонной аннигиляции
(2.47)
должна быть в =1/137 раз меньше. Однако позитроний может распадаться как по двухфотонному, так и трехфотонному каналам. Способ распада позитрония определяется тем, в каком спиновом состоянии возникает Ps при замедлении позитронов: парапозитроний испытывает двухфотонную аннигиляцию, ортопозитроний - трехфотонную. Причина, по которой пара- и ортопозитронии распадаются по-разному, связана с зарядовой симметрией КЭД и будет детально рассмотрена в параграфе 4. Здесь же мы воспримем это утверждение как данное и оценим вероятности аннигиляции пара- и ортопозитрония. Для этого воспользуемся формулой (2.29) для эффективного сечения аннигиляции на лету. В этой формуле, в соответствии с определением сечения через вероятность (см. Приложении к Гл.I о сечении) числитель r02 представляет собой вероятность процесса в единицу времени w, при условии, что поток сталкивающихся частиц равняется единице. В позитронии плотность налетающих частиц равняется по порядку величины
,
(2.48)
где aPs =1/ - борновский радиус позитрония, - приведенная масса.
Соответственно, вероятность двухфотонной аннигиляции позитрония дается формулой
65m.
(2.49)
Точный результат для парапозитрония имеет вид:
= 1/25m
= 0.81010c–1.
(2.50)
Соответственно, вероятность аннигиляции ортопозитрония по порядку величины должна даваться формулой
~
6m.
(2.51)
Результат точного расчета
=0.7107c–1.
(2.52)