
- •А.Н. Горитов
- •Учебное пособие
- •Учебное пособие
- •Введение
- •1 Введение в предмет
- •1.1 Непрерывная и дискретная информация
- •1.2 Данные и эвм
- •1.3 Объекты предметной области
- •1.4 Представление информации об объектах
- •1.5 Абстрактные алфавиты. Кодирование
- •2 Основные типы и структуры данных эвм
- •2.1 Архитектурные особенности эвм, наиболее существенные для представления данных
- •2.2 Основные понятия о типах и структурах данных
- •2.3 Массивы
- •2.4 Строки
- •2.5 Записи
- •2.6 Записи с вариантами
- •2.7 Множества
- •3 Последовательный файл
- •3.1 Основные свойства последовательных файлов
- •3.2 Сортировка последовательных файлов
- •4 Полустатические структуры
- •4.1 Стек, очередь и дек как полустатические структуры
- •4.2 Представление полустатических структур с помощью массивов
- •5 Линейные динамические структуры
- •5.1 Основные свойства динамических структур
- •5.2 Реализация связного списка массивом
- •5.3 Кольцевой связный список
- •5.4 Линейный двусвязный список
- •6 Представление динамических структур с помощью указателей
- •6.1 Указатели
- •6.2 Представление стека
- •6.3 Представление очереди
- •6.4 Ведение динамических списков с помощью указателей
- •6.5 Алгоритм составления кольцевого двусвязного списка
- •7 Древовидные структуры данных
- •7.1 Основные понятия и определения
- •7.2 Представление деревьев в эвм
- •7.3 Основные операции с бинарными деревьями
- •7.4 Сильно ветвящиеся деревья
- •8 Алгоритмы на графах
- •8.1 Машинное представление графов
- •8.2 Поиск в глубину в графе
- •8.3 Поиск в ширину в графе
- •8.4 Стягивающие деревья (каркасы)
- •8.5 Отыскание фундаментального множества циклов в графе
- •8.6 Эйлеровы пути в графе
- •8.7 Алгоритмы с возвратом
- •8.8 Нахождение кратчайших путей в графе
- •8.9 Кратчайшие пути от фиксированной вершины
- •8.10 Алгоритм Дейкстры
- •8.11 Пути в бесконтурном графе
- •Литература
7 Древовидные структуры данных
7.1 Основные понятия и определения
В задачах различного рода данные могут быть связаны между собой, не только образуя линейную последовательность (по горизонтали), но и иерархически (по вертикали, т.е. находиться на разных уровнях). Отношения типа предок-потомок являются иерархическими, тогда как брат-сестра - на одном уровне. Или такая иерархия:
Автомобиль
I
Агрегаты
! Узлы
i Детали
Деревом называется структура, которая характеризуется следующими свойствами:
существует единственный элемент, на который не ссылается никакой другой элемент. Этот элемент называется корнем.
каждый элемент связан с несколькими элементами следующего уровня иерархии. Эти элементы могут быть в свою очередь деревьями (поддеревьями).
3)каждый элемент промежуточного уровня порожден только одним элементом более высокого уровня. Элементы дерева, которые не ссылаются на другие элементы, являются терминальными (т.е. конечными)
или листьями. А элементы, не являющиеся терминальными, называются внутренними узлами.
Таким образом дерево отражает иерархически упорядоченную структуру данных, в которой прослеживаются связи между элементами предыдущего (верхнего) уровня или предками и элементами следующего уровня - потомками.
Можно считать список деревом, у которого каждый узел имеет не более одного "поддерева". Поэтому список называется также "вырожденным деревом".
Существует несколько способов изображения древовидной структуры. Например, пусть базовый тип Т есть множество букв. Древовидную структуру, образованную с какой-либо целью на таком типе можно изобра-
зить, например:
а) вложенными множествами (рис. 17);
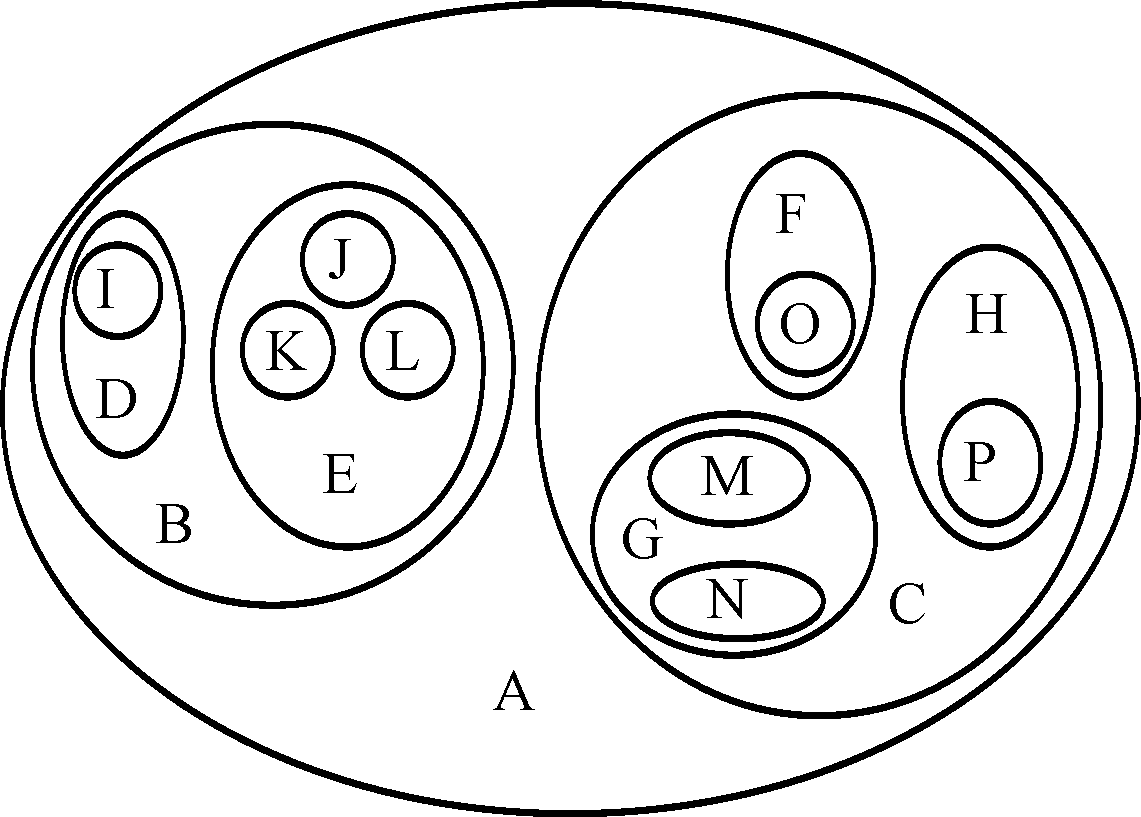
Рис. 17
б)вложенными скобками
(A(B(D(I), E(J, K, L)), C(F(O), G(M, N), H(P) )));
в)графом (рис. 18).
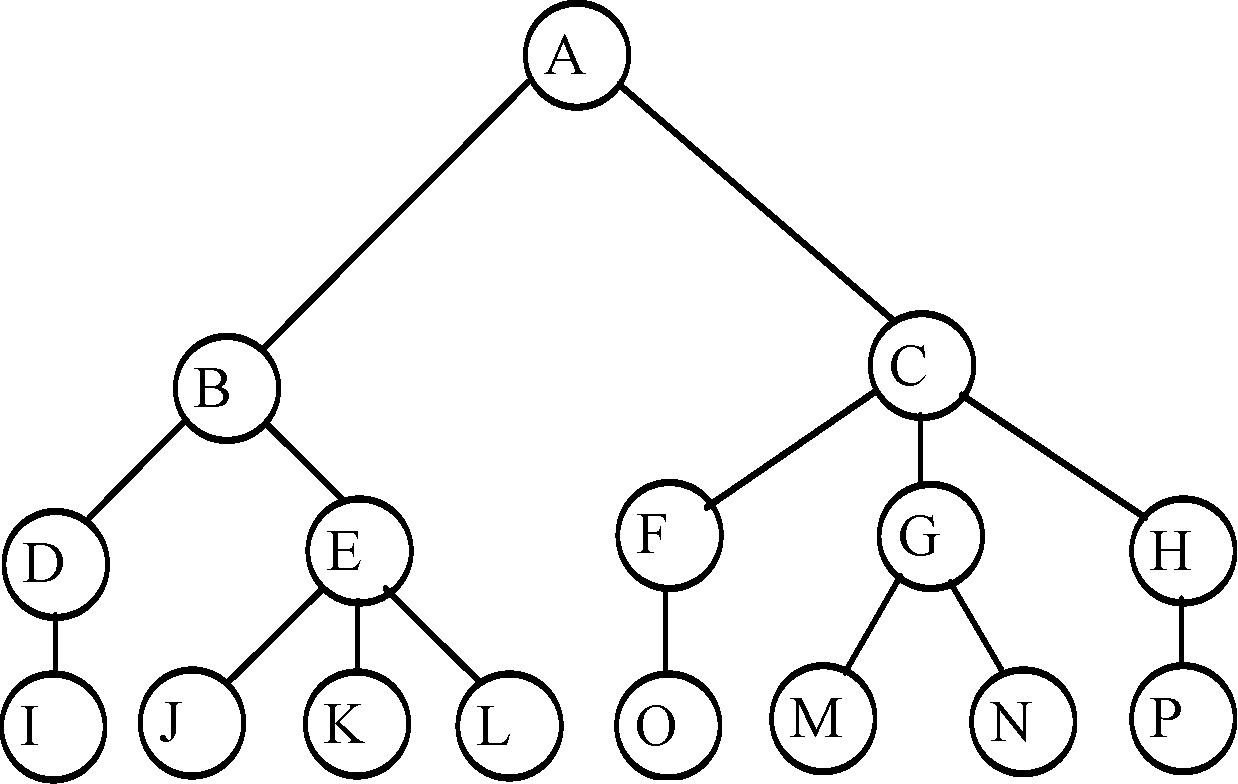
Рис. 18
Графом дерево представляется нагляднее, но вверх ногами (корнем).
Узлы располагаются по уровням. Корень – нулевой уровень и т.д. Максимальный уровень какого-либо элемента дерева называется его глубиной или высотой.
Число непосредственных потомков внутреннего узла называется его степенью. Максимальная степень всех узлов есть степень дерева. Наше дерево – дерево третьей степени.
Число ветвей или ребер, которые нужно пройти, чтобы продвинуться от корня к узлу х, называется длиной пути к х. Корень имеет длину пути 0, его непосредственные потомки – длину пути 1 и т.д. Вообще узел на уровне i имеет длину пути i.
Длина пути дерева – это сумма длин путей всех его узлов. Она также называется длиной внутреннего пути. Для нашего дерева длина пути равна 36. Средняя длина пути
1
Pc
ср
П
Hni-
i = \
где ni – число узлов на уровне i; n – число элементов.
Дерево, у которого ветви каждого узла упорядочены, называется упорядоченным деревом:

Особо важную роль играют упорядоченные деревья второй степени. Они называются бинарными деревьями или двоичными. Бинарное дерево – это конечное множество элементов (узлов), каждый из которых либо пуст (не связан с нижним уровнем, не имеет потомков, т.е. лист), либо является корнем (или узлом) с двумя различными бинарными поддеревьями – левым и правым.
Деревья, имеющие степень больше двух, называются сильно ветвящимися деревьями.
Пример бинарного дерева – Арифметическое выражение с двуместными операциями, где каждая операция – это ветвящийся узел с операндами в качестве поддеревьев, например выражение (a + b / c) * (d - e * f), представится в виде двоичного дерева следующим образом

В принципе, любое n–арное дерево может быть преобразовано в эквивалентное ему бинарное дерево.
