
- •Введение
- •Рабочая программа по дисциплине
- •Список рекомендуемой литературы Основная литература
- •Дополнительная литература
- •Рейтинговая система оценки успеваемости
- •5. Контрольные работы
- •6. Индивидуальные задания
- •Входной и выходной токи связаны с токами невырожденных контуров выражениями
- •Подпрограмма удаления из матрицы м
- •Определение ачх коэффициента передачи по напряжению
- •Входное и выходное напряжения связаны с напряжениями главных сечений выражениями
- •Расчет ачх и фчх избирательного rc-усилителя
- •Так как при нумерации главных сечений сначала следуют невырожденные сечения, а затем вырожденные, матрица главных сечений имеет вид:
- •Входной и выходной токи связаны с компонентами вектора токов z-ребер выражениями:
- •Входной и выходной токи связаны с токами независимых контуров выражениями
- •Система координат представляет собой совокупность независимых сечений. Выберем каноническую систему сечений, обозначенную на рис. 6.21.
- •Система координат представляет собой совокупность независимых контуров. Выберем каноническую систему контуров, обозначенную на рис. 6.27. Матрица независимых контуров имеет размерность :
- •Расчет ачх и фчх избирательного rc-усилителя
- •Матрица проводимостей пассивной части схемы
- •В результате система вк-уравнений может быть преобразована:
- •7. Коллоквиум
- •Вопросы коллоквиума
- •8. Экзамен
- •Эквивалентные схемы активных электронных компонентов
Входной и выходной токи связаны с токами невырожденных контуров выражениями
![]() ,
,
![]() ,
,
которые могут быть представлены в виде матричного уравнения:
 ,
(6.12)
,
(6.12)
где
 ,
,  .
.
Объединив (6.10) и (6.12) в одно матричное уравнение

и
решив его относительно ![]() и
и ![]() ,
получим
,
получим
 (6.13)
(6.13)
Сравнивая (6.13) с (6.5) получаем выражения, связывающие z-параметры четырехполюсника с матрицей эквивалентных параметров схемы:
 ,
,
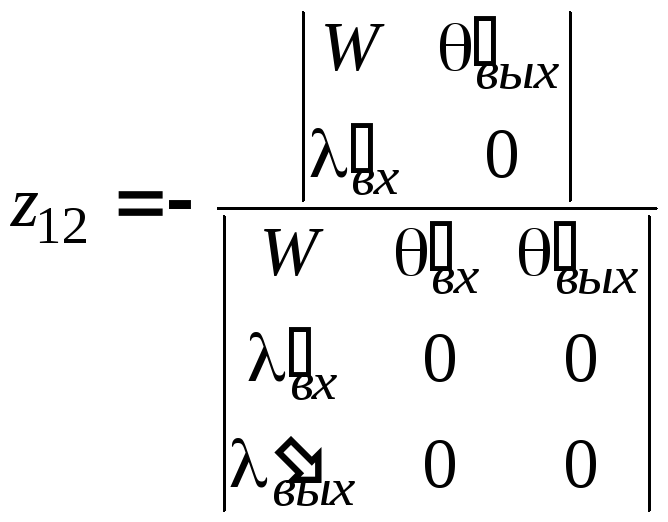 ,
,
(6.14)
 ,
,
 .
.
Так как элементами
матриц
![]() ,
,![]() ,
,![]() ,
,![]() являются значения 1, -1, 0, то определители,
стоящие в числителях выражений (6.14)
могут быть приведены к определителям
(n-1)-го порядка, а
определитель, стоящий в знаменателе
этих выражений – к определителю (n-2)-го
порядка, гдеn– порядок
матрицы
являются значения 1, -1, 0, то определители,
стоящие в числителях выражений (6.14)
могут быть приведены к определителям
(n-1)-го порядка, а
определитель, стоящий в знаменателе
этих выражений – к определителю (n-2)-го
порядка, гдеn– порядок
матрицы![]() .
.
Определитель
матрицы ![]() равен суммарному
алгебраическому дополнению матрицы
равен суммарному
алгебраическому дополнению матрицы
![]() относительно преобразующих векторов
относительно преобразующих векторов![]() и
и![]() с обратным знаком:
с обратным знаком:
![]() .
(6.15)
.
(6.15)
Обычно
векторы
![]() и
и![]() содержат значительное число нулевых
составляющих. Поэтому эти векторы чаще
всего отображают множеством номеров
их ненулевых составляющих, разбивая
каждое из них на подмножества номеров
положительных и отрицательных
составляющих, называемых положительными
и отрицательными подмножествами.
содержат значительное число нулевых
составляющих. Поэтому эти векторы чаще
всего отображают множеством номеров
их ненулевых составляющих, разбивая
каждое из них на подмножества номеров
положительных и отрицательных
составляющих, называемых положительными
и отрицательными подмножествами.
Суммарное
алгебраическое дополнение ![]() матрицы
матрицы
![]() относительно преобразующих векторов
относительно преобразующих векторов![]() и
и![]() получают следующим образом:
получают следующим образом:
Выбирают опорный элемент
 в преобразующем векторе
в преобразующем векторе .
Прибавляютp-ую
строку матрицы
.
Прибавляютp-ую
строку матрицы
 к строкам, определяемым элементами
подмножества противоположного знака,
и вычитаютp-ую
строку из строк, определяемых элементами
подмножества того же знака, что и опорный
элемент. После этого p-ую
строку вычеркивают.
к строкам, определяемым элементами
подмножества противоположного знака,
и вычитаютp-ую
строку из строк, определяемых элементами
подмножества того же знака, что и опорный
элемент. После этого p-ую
строку вычеркивают.Выбирают опорный элемент
 в преобразующем векторе
в преобразующем векторе Прибавляютq-ый
столбец матрицы
Прибавляютq-ый
столбец матрицы
 к столбцам, определяемым элементами
подмножества противоположного знака,
и вычитаютq-ый
столбец из столбцов, определяемых
элементами подмножества того же знака,
что и опорный элемент. После этого q-ый
столбец вычеркивают.
к столбцам, определяемым элементами
подмножества противоположного знака,
и вычитаютq-ый
столбец из столбцов, определяемых
элементами подмножества того же знака,
что и опорный элемент. После этого q-ый
столбец вычеркивают.Находят определитель преобразованной матрицы (n-1)-го порядка.
Результат умножают на
 ,
где
,
где - знак произведения опорных элементов;
p
и q
– номера опорных строки и столбца.
- знак произведения опорных элементов;
p
и q
– номера опорных строки и столбца.
Определитель
матрицы  равен двухкратному
равен двухкратному
суммарному
алгебраическому дополнению матрицы
![]() относительно преобразующих векторов
относительно преобразующих векторов![]() ,
,![]() и
и![]() ,
,![]() :
:
 .
(6.16)
.
(6.16)
Множества
номеров ненулевых составляющих векторов
![]() и
и
![]() (как и векторов
(как и векторов
![]() и
и
![]() )
могут содержать общую часть, определяемую
их пересечением, и собственные
подмножества, включающие те элементы,
номера которых имеются только в таком
векторе. На первом этапе определения
)
могут содержать общую часть, определяемую
их пересечением, и собственные
подмножества, включающие те элементы,
номера которых имеются только в таком
векторе. На первом этапе определения ![]() опорные элементы
в преобразующих векторах следует
выбирать из тех, которые содержатся в
собственных подмножествах. Невозможность
такого выбора указывает на линейную
зависимость векторов
опорные элементы
в преобразующих векторах следует
выбирать из тех, которые содержатся в
собственных подмножествах. Невозможность
такого выбора указывает на линейную
зависимость векторов
![]() и
и
![]() (или векторов
(или векторов
![]() и
и
![]() ),
следствием чего является равенство
нулю двухкратного алгебраического
дополнения
),
следствием чего является равенство
нулю двухкратного алгебраического
дополнения ![]() .
.
Двухкратное
суммарное алгебраическое дополнение
![]() матрицы
матрицы
![]() относительно преобразующих векторов
относительно преобразующих векторов![]() ,
,![]() и
и![]() ,
,![]() получают следующим образом:
получают следующим образом:
Выбирают опорный элемент
 в преобразующем векторе
в преобразующем векторе .
Прибавляют
.
Прибавляют -ую
строку матрицы
-ую
строку матрицы к строкам, определяемым элементами
подмножества противоположного знака,
и вычитают
к строкам, определяемым элементами
подмножества противоположного знака,
и вычитают -ую
строку из строк, определяемых элементами
подмножества того же знака, что и опорный
элемент. После этого
-ую
строку из строк, определяемых элементами
подмножества того же знака, что и опорный
элемент. После этого -ую
строку вычеркивают.
-ую
строку вычеркивают.Выбирают опорный элемент
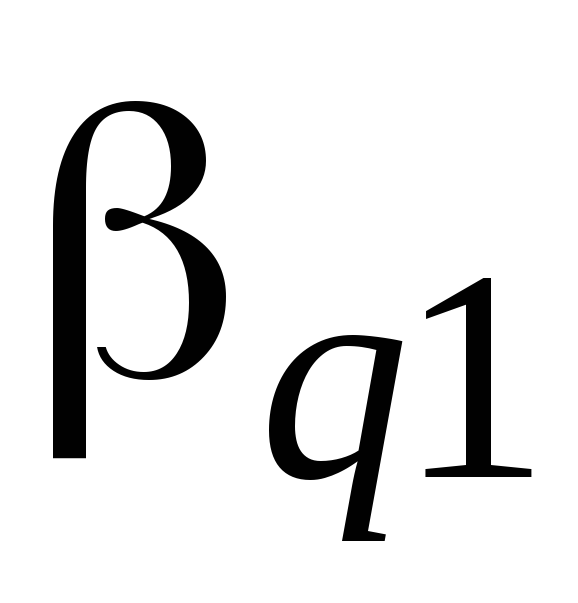 в преобразующем векторе
в преобразующем векторе Прибавляют
Прибавляют -ый
столбец матрицы
-ый
столбец матрицы к столбцам, определяемым элементами
подмножества противоположного знака,
и вычитают
к столбцам, определяемым элементами
подмножества противоположного знака,
и вычитают -ый
столбец из столбцов, определяемых
элементами подмножества того же знака,
что и опорный элемент. После этого
-ый
столбец из столбцов, определяемых
элементами подмножества того же знака,
что и опорный элемент. После этого -ый
столбец вычеркивают.
-ый
столбец вычеркивают.Выбирают опорный элемент
 в преобразующем векторе
в преобразующем векторе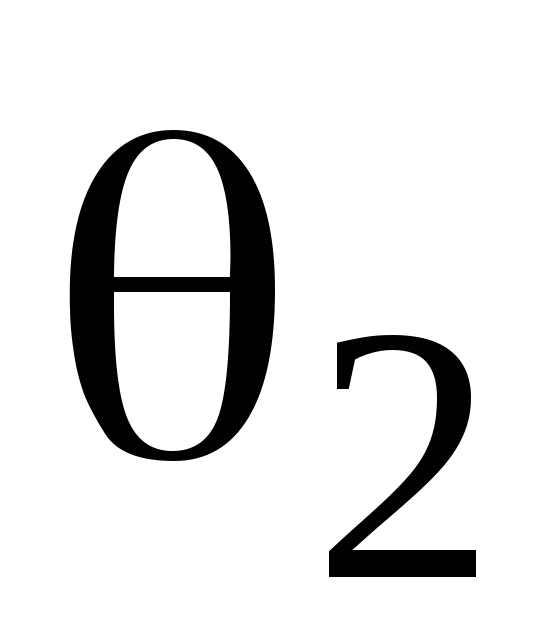 .
Прибавляют
.
Прибавляют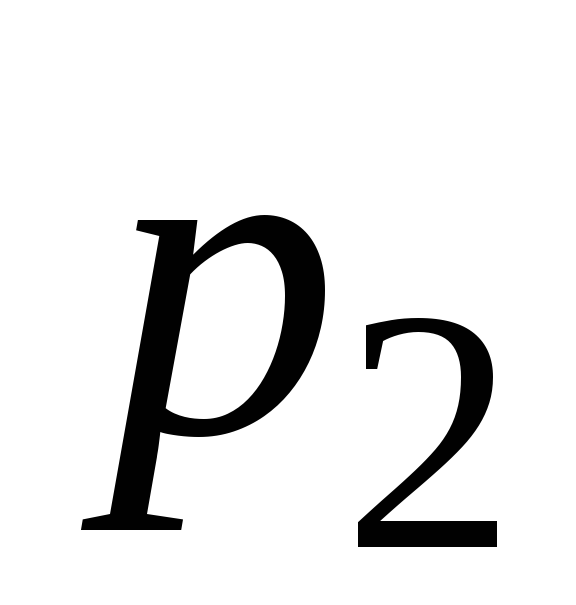 -ую
строку матрицы
-ую
строку матрицы к строкам, определяемым элементами
подмножества противоположного знака,
и вычитают
к строкам, определяемым элементами
подмножества противоположного знака,
и вычитают -ую
строку из строк, определяемых элементами
подмножества того же знака, что и опорный
элемент. После этого
-ую
строку из строк, определяемых элементами
подмножества того же знака, что и опорный
элемент. После этого -ую
строку вычеркивают.
-ую
строку вычеркивают.Выбирают опорный элемент
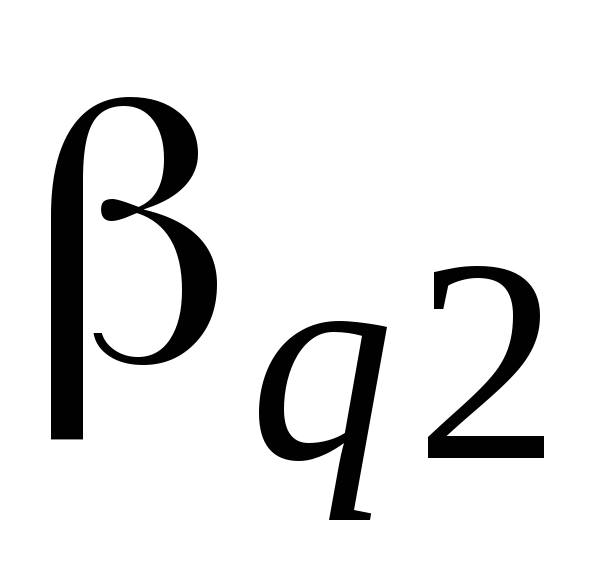 в преобразующем векторе
в преобразующем векторе Прибавляют
Прибавляют -ый
столбец матрицы
-ый
столбец матрицы к столбцам, определяемым элементами
подмножества противоположного знака,
и вычитают
к столбцам, определяемым элементами
подмножества противоположного знака,
и вычитают -ый
столбец из столбцов, определяемых
элементами подмножества того же знака,
что и опорный элемент. После этого
-ый
столбец из столбцов, определяемых
элементами подмножества того же знака,
что и опорный элемент. После этого -ый
столбец вычеркивают.
-ый
столбец вычеркивают.Находят определитель преобразованной матрицы (n-2)-го порядка.
Результат умножают на
 ,
где
,
где - знак произведения
опорных элементов;
- знак произведения
опорных элементов;
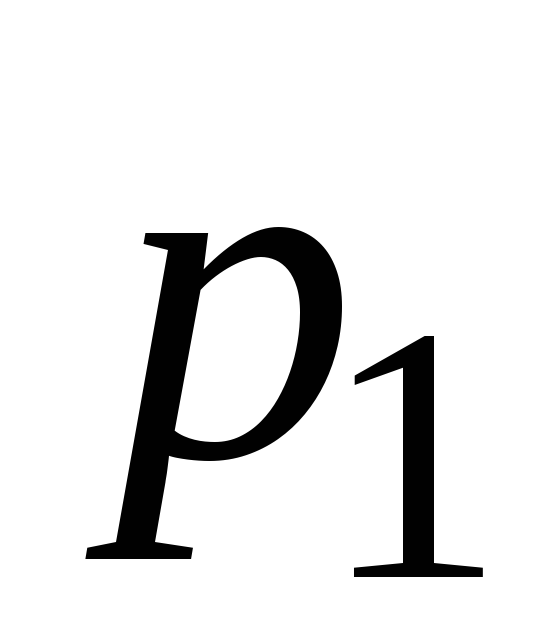 ,
, ,
, ,
, – номера опорных строк и столбцов;
– номера опорных строк и столбцов;
 .
.
Учитывая (6.15) и (6.16), выражения (6.14) для z-параметров могут быть представлены в виде:
 ,
,
 ,
,
(6.17)
 ,
,
 .
.
Подставляя
(6.17) в выражения (6.7)-(6.9) и учитывая, что
![]() ,
получаем:
,
получаем:
 ,
(6.18)
,
(6.18)
 ,
(6.19)
,
(6.19)
 .
(6.20)
.
(6.20)




Обобщенные топологические матрицы:
![]()
![]()

![]()

Компонентные матрицы:



Обобщенная компонентная матрица:
![]()
Матрица эквивалентных параметров схемы:
![]()
Столбцы матрицы невырожденных контуров,
соответствующие входному и выходному ребрам

Преобразующие векторы для суммарных
алгебраических дополнений матрицы W
![]()
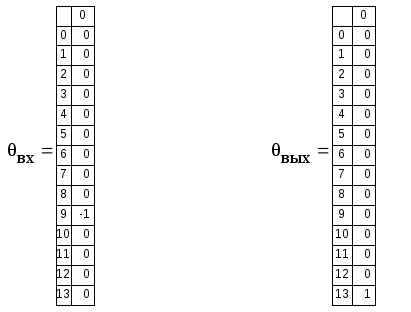
![]()

