Формула определения координат вектора для плоских задач

В случае плоской задачи вектор AB заданный координатами точек A(A_x ; A_y) и B(B_x ; B_y) можно найти воспользовавшись следующей формулой

AB = {B_x - A_x ; B_y - A_y}

Формула определения координат вектора для пространственных задач

В случае пространственной задачи вектор AB заданный координатами точек A(A_x ; A_y ; A_z) и B(B_x ; B_y ; B_z) можно найти воспользовавшись следующей формулой

AB = {B_x - A_x ; B_y - A_y ; B_z - A_z}

Формула определения координат вектора для n -мерного пространства

В случае n-мерного пространства вектор AB заданный координатами точек A(A₁ ; A₂ ; ... ; A_n) и B(B₁ ; B₂ ; ... ; B_n) можно найти воспользовавшись следующей формулой

AB = {B₁ - A₁ ; B₂ - A₂ ; ... ; B_n - A_n}

49. Определение ранга матрицы через миноры.

Метод элементарных преобразований

Используя свойства матрицы связанные с ее рангом, получен метод расчета ранга наиболее часто использующийся на практике.

Метод 1: Ранг матрицы равен количеству ненулевых строк после приведения матрицы к ступенчатому виду, используя элементарные преобразования над строками и столбцами матрицы.

Метод окаймления миноров

Теорема: Ранг матрицы равен наибольшему порядку не равного нулю минора.

Метод 2: Если в матрице A найден ненулевой минор k-го порядка M. Рассмотрим все миноры (k + 1)-го порядка, включающие в себя (окаймляющие) минор M; если все они равны нулю, то ранг матрицы равен k. Если среди окаймляющих миноров найдется ненулевой, то вся процедура повторяется.

50. Определение базисного минора, базисных строк и столбцов матрицы.

В матрице порядка mxn минор порядка r называется базисным, если он не равен нулю, а все миноры порядка r+1 и выше равны нулю, или не существуют вовсе, т.е. r совпадает с меньшим из чисел m или n.  Столбцы и строки матрицы, на которых стоит базисный минор, также называются базисными.

51. Теорема о базисном миноре.

Теорема 1.6 (теорема о базисном миноре). Базисные строки (базисные столбцы) линейно независимы. Любая строка (любой столбец) матрицы А является линейной комбинацией базисных строк (базисных столбцов). 

52. Теорема о необходимых и достаточных условиях равенства нулю определителя.

Для равенства определителя нулю необходимо и достаточно, чтобы его столбцы (строки) были линейно зависимыми.

Пример №2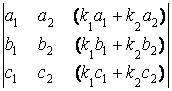0

 = 0

Третий столбец данного определителя представляет линейную комбинацию первого и второго столбцов с коэффициентами K1 и K2 . Поэтому столбцы данного определителя линейно зависимы (выполнено необходимое и достаточное условие равенства определителя нулю).

Пример №21. Исследование системы столбцов

=, =, =

На линейную зависимость с помощью определителя

 = 1*2*3 + 0*2*2 + 1*0*1 – 1*2*2 – 0*0*3 – 1*2*1 = 0 Определитель равен нулю, следовательно – столбцы линейно зависимы.

53. Элементарные преобразования матрицы.

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц, то есть, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.