Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

matan4_bel

.pdf

Скачиваний:

Добавлен:

10.05.2015

Размер:

6.91 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

f (z)

ТФКП (мат. анализ часть 4) семестр 4, лекция 8, стр. 5 из 6

4.Основная теорема о вычетах.

1.Основная теорема о вычетах.

Теорема 4.

Пусть f (z) регулярна в конечной односвязной области D за

исключением

конечного

числа

изолированных

особых

точек

z1, z2 ,...., zn , а γ

- замкнутая кривая, лежащая в D и содержащая

z1, z2 ,...., zn

внутри себя (см. рис. 4.1.1). Тогда:

∫ f (z)dz = 2πi∑resz

f (z)

k=1 k

Доказательство:

рис. 4.1.1.

Из теоремы Коши для многосвязной области следует:

∫

f (z)dz =

f (z)dz +

f (z)dz +...+

f (z)dz =

= 2πi

∑

2πi res f (z) + res f (z) +

...+ res f (z)

res f (z) .

γ1

γ 2

γ n

k=1 k

Ч.т.д.

Пример (задача из Типового расчета):

Вычислить:

∫γ

z(z + 2)(z + 4)

γ : а) γ

= 1; б) γ

= 3; в)

= 5; г) γ

z − 2

;

res f (z) = lim

;

(z + 2)(z + 4)

z→0

res f (z) = lim

= −

;

−2

z→−2 z(z + 4)

res f (z) = lim

;

−4

z→−4 z(z + 2)

Тогда:

а)

∫

f (z)dz = 2πires f (z) =

2πi

= πi ;

рис. 4.1.2.

γ1

б) ∫

γ2

в) ∫

γ3

г) ∫

γ4

				1		1				πi
f (z)dz = 2πi(res f (z) + res f (z))= 2πi			−		+		= −					;
f (z)dz = 2πi(res f (z) + res f (z))= 2πi			−	4	+	8	= −				4	;
0	−2			4		8					4
0	−2
								1			1		1
f (z)dz = 2πi(res f (z) + res f (z) + res f (z))= 2πi									−			+		= 0;
f (z)dz = 2πi(res f (z) + res f (z) + res f (z))= 2πi								8	−		4	+	8	= 0;
0	−2	−4						8			4		8
0	−2	−4

f (z)dz = 0, т.к. внутри γ4 f (z) регулярна.

2. Вторая теорема о вычетах. Теорема 5. О полной сумме вычетов.

Пусть регулярна в расширенной комплексной плоскости за исключением конечного числа изолированных особых точек, считая точку z = ∞ . Тогда:

∑res f (z) = 0

k=1 zk

z1, z2 ,...., zn−1 - конечные особые точки f (z) , zn - бесконечная точка.

ТФКП (мат. анализ часть 4) семестр 4, лекция 8, стр. 6 из 6

Доказательство:

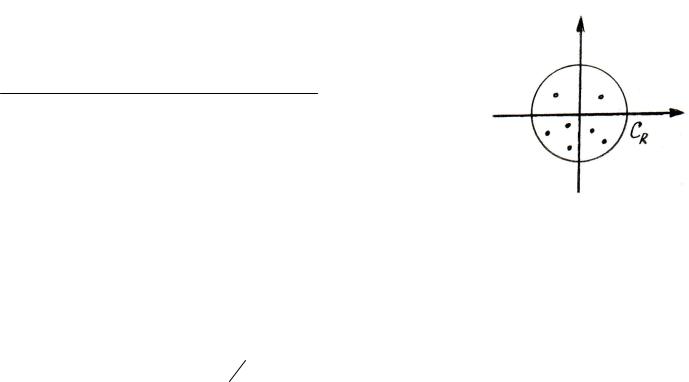
Возьмем такую большую окружность, чтобы все особые точки, кроме ∞ , лежали

внутри. Назовем ее CR

(см. рис. 4.2.2):

n−1

= R

∫

f (z)dz = 2πi

∑ z

∫

∞

resf (z) = −

f (z)dz = −2πi resf (z)

k=1

т.к. вычет в бесконечности: res f (z) =∞

1
1	∫		f (z)dz
2πi	∫		f (z)dz
2πi
	C	R
	C

n−1

2πi∑resf (z) + 2πires f (z) = 0

k=1 zk

∞

Ч.т.д.

3. Вычисление контурных интегралов.

Теорема о полной сумме вычетов облегчает вычисление

рис. 4.2.2.

контурных интегралов.

Пример:

∫

= J = ?

z(z4 +1)

(1− z4 + z8 −...)=

− z3 + z7 −...

res f (z) = 1;

z(z

+1)

z z

1 z

1−

−... =

−

−...

z(z4 +1)

4 +

z z

1 z5

+ 1z4

z11

= {

> 1}= t5 − t9 + t11 −..., где

t =

res f (z) = 0

t = 0 ↔ z = ∞

∞

res f (z) + res f (z) + res f (z) + res f (z) + res f (z) + res f (z) = 0

∞

res f (z) + ∑resf (z) = − res f (z) = 0

J = 2πi 0 = 0

k=1

∞

ТФКП (мат. анализ, часть 4), семестр 4, лекция 9 – 10, стр. 1 из 7

Применение вычетов к вычислению интегралов.

1. Интегралы по неограниченным путям интегрирования.

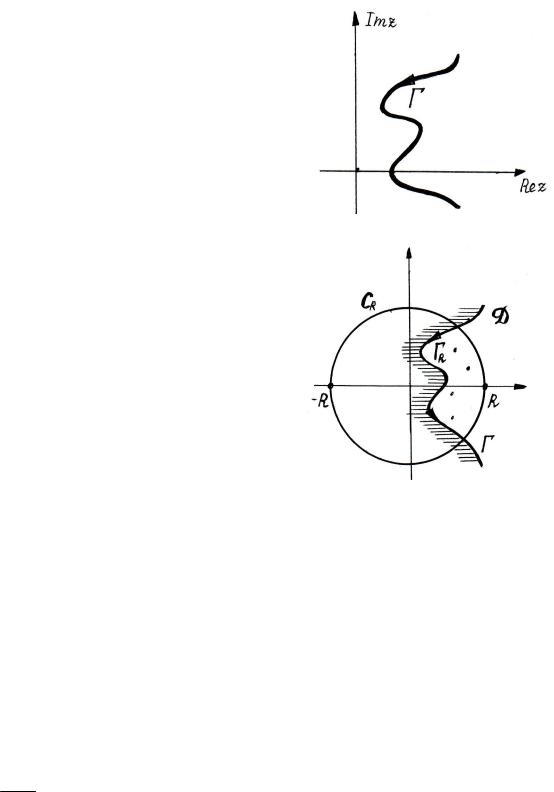
Пусть Г – неограниченная гладкая кривая (гладкий путь) – см. рис. 1.1.

Определение.
∫ f (z)dz = Rlim→∞ ∫ f (z)dz ,
Γ	ΓR

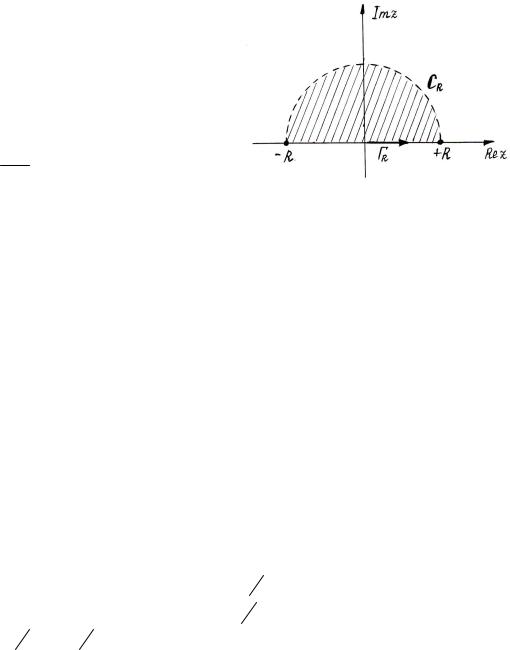
где ΓR - часть пути, лежащая внутри окружности CR радиуса R с центром в точке О (см. рис. 1.2).

Теорема.

1) Пусть f(z) регулярна в D, ограниченной Г, за исключением конечного числа изолированных особых точек z1, z2 ,..., zn и существует ∫ f (z)dz .

					Γ
2) lim	R max			f (z)	= 0 .
2) lim	R max			f (z)	= 0 .
			R
R→∞		C

		n
1),	2) ∫ f (z)dz = 2πi∑resf (z)		(т.е.	применима
	Γ	k=1 zk
теорема о вычетах).
	Доказательство:
Возьмем достаточно большое R, чтобы все zk лежали
внутри контура γ = ΓR + CR . Тогда:
		n
	∫ f (z)dz = 2πi∑resz f (z) .
	γ	k=1 k
		n
Следовательно, ∫		f (z)dz = 2πi∑resz f (z)		не зависит от
	ΓR +CR	k=1	k
R. Следовательно,
					n
Rlim→∞ ∫	f (z)dz = Rlim→∞ ∫ f (z)dz + Rlim→∞ ∫ f (z)dz = ∫ f (z)dz + Rlim→∞ ∫				f (z)dz = 2πi∑resz f (z) .
ΓR +CR	ΓR	CR	Γ	CR	k=1 k

рис. 1.1.

рис. 1.2.

Первое слагаемое получено по определению. Докажем, что второе слагаемое равно

нулю. Рассмотрим lim

f (z)dz

= lim

f (z)

≤ lim max

f (z)

2π R = 2π 0 = 0 (использовалась

R→∞

∫

R→∞ ∫

R→∞ C

теорема об оценке определенного интеграла и условие 2) теоремы). Следовательно,

∫ f (z)dz = 2πi∑res f (z) .

k=1 zk

Ч.т.д.

Следствие:

(вычисление интегралов по вещественной оси от дробно-рациональных функций)

1) Пусть f (x) = Pm (x) - рациональная дробь.

Qk (x)

2) k − m ≥ 2 (степень числителя по крайней мере на 2 меньше степени знаменателя).

3) Qk (x) не имеет нулей на вещественной оси.

	+∞	Pm (x)	n		Pm (z)
1), 2), 3)	∫		dx = 2πi∑res			по всем zp
		Q (x)
			p=1	zp	Q (z)
	−∞	k			k

ТФКП (мат. анализ, часть 4), семестр 4, лекция 9 – 10, стр. 2 из 7

- особенностям, лежащим в верхней

полуплоскости ( zp {Im z > 0} ) Доказательство следствия:

P (x)

(A = const)

+∞ P(x)dx

+∞ Adx

k − m ≥ 2

≤

∫

≤ ∫

Q (x)

Q(x)

−∞

Следовательно, интеграл сходится по признаку сравнения несобственных интегралов I-го

рода.

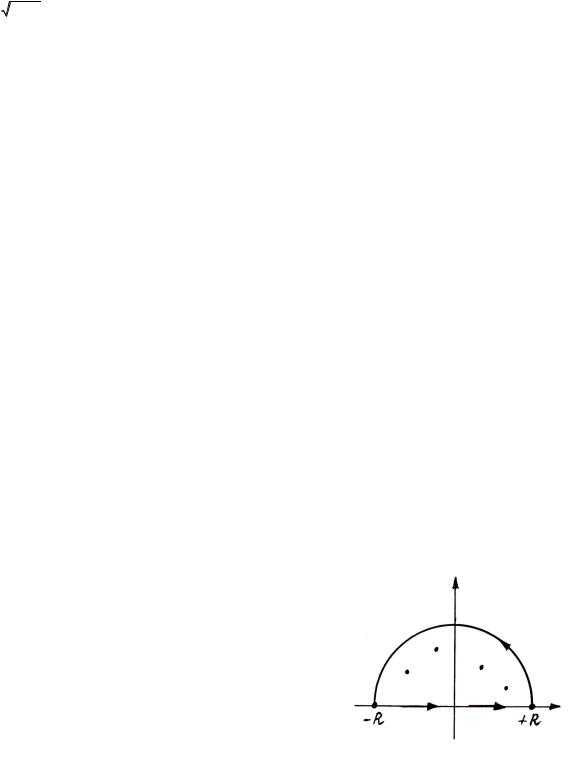
Пусть

ΓR = (−R; + R) ,

а Γ = (−∞; + ∞)

- см. рис. 1.3.

P(z)

≤ Rmax

= R

= R ).

Тогда Rmax

(т.к. на CR

Q(z)

Следовательно,

lim Rmax

f (z)

= lim

т.е. условия

= 0,

R→∞

R→∞ R

теоремы выполнены, и отсюда следует:

	P(z)dz	=	+∞	P(x)dx	= 2πi	res
∫Γ			−∞∫
	Q(z)			Q(x)		∑ zp

т.к. на Γ: z≡x

верхней полуплоскости.

P(z) , где zp внутри D, т.е. в

Q(z)

рис. 1.3.

Ч.т.д.

Примеры:

+∞

x2dx

+∞

x2dx

2πi (resi f (z) + res2i

f (z))=

∫

πi

−

= πi

−

1)(x

+ 4)

+1)(x

−∞ (x

6 3

> 0

res f (z) = lim

= −

;

(z2

+ i)(z2 +

z→i

3 2i

res f (z) = lim

−1

= −

;

+1)(z2 +

2i)

z→2i (z2

−3i

т.к. i и 2i – простые полюса.

Покажем преимущество такого решения перед «обычным»:

Ax + B

Cx + D

(x2 +1)(x2 + 4)

x2 +1

x2 + 4

(

Ax + B

)(

+ 4

)

(

Cx + D

)

(

)

= x2

A+ C = 0

B + D = 1

= −

A = C =

x1 : 4A+ C = 0

: 4B + D = 0

= 4

+∞

+∞ − 1

+∞

1 π

2 π

∫

= ∫

∫

= −

dx +

dx = −

arctg x +

arctg

= −

− 0

1)(x

+ 4)

+ 4

3 2

6 3 6

+∞

∫

= 2πires f (z) = 2πi

(x2

+ 4x +

13)

−∞

Нули знаменателя:

ТФКП (мат. анализ, часть 4), семестр 4, лекция 9 – 10, стр. 3 из 7

z2 + 4z +13 = 0

z = −2 ± 4 −13 = −2 ± 3i

= −2 + 3i принадлежит верхней полуплоскости

z0 - полюс II-го порядка

′

−2

res f (z) = lim

z→−2+3i (z + 2 + 3i)2

(z + 2 + 3i)3

z= z0

63 i3

63 i

2. Лемма Жордана.

Формулировка леммы:

1) f(z)

– регулярна в верхней полуплоскости (Im z ≥ 0) за исключением конечного

числа изолированных особых точек.

2) max

f (z)

→ 0 при

R → ∞ , где CR - полуокружность радиуса R с центром в точке

z = 0, лежащая в верхней полуплоскости.

1), 2)

λ > 0

lim

∫

f (z)eiλzdz = 0.

R→∞

Следствие:

+∞

dx)

(вычисление интегралов вида ∫ R(x) cosλx

−∞

sinλx

Пусть

R(x) =

Pm (x)

правильная дробь (m < k ),

Q(x) ≠ 0 на

вещественной

оси и

Qk (x)

+∞

z1, z2 ,..., zn - нули Q(z) в верхней полуплоскости. Тогда ∫ R(x)eiλxdx = 2πi∑resR(z)eiλz , а т.к.

−∞

p=1 zp

+∞

iλz

+∞

2πi∑resR(z)e

iλz

iλx

= cosλx + isinλx , то

∫ R(x)sinλxdx

= Im

∫ R(x)cosλxdx = Re 2πi∑resR(z)e

−∞

Доказательство следствия:

Возьмем контур, как на рис. 2.1.

∫ R(z)eiλzdz + ∫ R(z)eiλzdz = 2πi∑resR(z)eiλz

не зависит от R

−R

p=1 zp

при R → ∞ .

В силу леммы

lim

∫ R(z)eiλzdz = 0, т.к.

max

R(z)

≤

→ 0

при R → ∞

R→∞

(т.к. дробь правильная)

+∞

Rlim→∞ ∫ R(z)eiλzdz = ∫ R(x)eiλxdx = 2πi∑resR(z)eiλz

рис. 2.1

−R

−∞

(т.к. на вещественной оси z ≡ x)

Ч.т.д.

ТФКП (мат. анализ, часть 4), семестр 4, лекция 9 – 10, стр. 4 из 7

Примеры:

+∞

cosax

dx = (в силу четности)

+∞

cosax

+∞

cosax

+∞

sin ax

+∞ cosax + isin ax

∫

dx +

∫

dx =

∫

dx =

+ b

−∞ x

−∞

+∞

eiax

eiaz

eia bi

∫

dx =

2πi res

= πi

= π i

e−ab

+ b

+ bi

−∞ x

bi z

z=bi

2b i

+∞

(x3 +1)sin x

∫

dx = π

−

+10x

−∞

8 e

Рассмотрим

+∞

x3 +1

dx = 2πi(res R(z)e

∫

+ res R(z)e

+10x

−∞

t2 +10t + 9 =

t = −1, t = −9

= −1

x = ±i

= −9

x = ±3i

−27i +1

−i +1

−27i +1

−i +1

2πi

e−3 +

2i 8

e−1

= π

−24

e−3 +

e−1

−8 3 2i

z0 =a0 +ib0

reslim

z3 +1

eiz = −i +1e−1;

(z + i)(z2 + a)

z→i

2i 8

reslim

z3 +1

eiz = −27i +1e−3;

(z +1)(z2 + 3i)

3i z→3i

−6i 8

e−3

e−1

π 1

+∞

Re(z0 ) = π

−

∫ R(x)cos xdx

−24

8 e 3e

−∞

−27

+∞

Im(z0 ) = π

e−3 +

e−1 =

−

∫ R(x)sin xdx

−24

−∞

Ответ: π

−

8 e

2π

3. Вычисление интегралов вида ∫ R(sin x,cos x)dx с помощью

вычетов.

Пусть

R(u,v) - рациональная функция двух переменных. Пусть u = sin x, v = cos x .

Произведем замену z = eix . Тогда:

idz

eix + e−ix

z +

;

sin x =

eix − e−ix

z −

dz = ieixdx

dx = −

;

cos x =

Если х изменяется от 0 до 2π , то z = eix

движется по окружности

=1 против часовой

стрелки и

2π

R(sin x,cos x)dx =

z +

z −

idz

∫

;

−

ТФКП (мат. анализ, часть 4), семестр 4, лекция 9 – 10, стр. 5 из 7

Пример:

2π

2i −

2dz

−

∫ 5+ 4sin x

∫

z2 −1

∫

10iz + 4z2 −

∫

2z2 + 5iz − 2

z −

=110i + 4

5+ 4

= −5i ± 3i

;

= −2i;

= −

- лежит внутри контура.

1,2

=2πires

= 2πi

2πi

2π

2z2 + 5iz − 2

−

4z +

z=−

−

4. Принцип аргумента.

Пусть f(z) регулярна в D ΓD

за исключением конечного числа полюсов z1, z2 ,..., zn ,

лежащих в D (но не на ΓD ) и на Γ :

f (z) ≠ 0 .

Определение.

Функция ϕ(z) =

f ′(z)

= [ln f (z)]′

называется логарифмической производной.

f (z)

Функция res

f ′(z)

называется логарифмическим вычетом, где zk

- все особые точки ϕ(z) ,

zk f (z)

т.е. a1, a2 ,..., am - полюса f(z) и b1, b2 ,..., bp

- нули f(z).

zk = {a1, a2 ,..., am , b1, b2 ,..., bp}.

res

f ′(z)

∫

f ′(z)

dz - логарифмический вычет f(z) относительно контура Г.

f (z)

2πi Γ f (z)

Теорема.

Если f(z) имеет в точке

z = z0

нуль

порядка n или полюс порядка k, то

логарифмическая производная

ϕ(z) =

f ′(z)

имеет в этой точке простой полюс и вычет в

f (z)

нем равен: res

f ′(z)

= n (в случае нуля), либо res

f ′(z)

= −k

(в случае полюса).

z0 f (z)

f (z)

Доказательство:

а) f(z) имеет в z0

нуль порядка n. Следовательно:

f (z) = (z − z

f (z),

f (z

) ≠ 0

ln f (z) = nln(z − z

) + ln f (z)

ϕ(z) = (ln f (z))′

′(z)

f ′(z)

(

≠ 0)

f (z

)

f (z)

z − z0

f1(z)

ϕ(z) имеет в z0

простой полюс и С-1

= n.

б) f(z) имеет в z0 полюс порядка k. Следовательно:

(z)

ln f (z) = ln f2 (z) − k ln(z − z0 )

f ′(z)

f (z) =

−

(z − z

f (z)

f2 (z)

(z − z0 )

в z0 простой полюс и C−1 = −k.

Ч.т.д.

ТФКП (мат. анализ, часть 4), семестр 4, лекция 9 – 10, стр. 6 из 7

Теорема.

Если f(z) регулярна в D ΓD за исключением конечного числа полюсов и f (z) ≠ 0, ≠ ∞

на

ΓD , то:

∫

f ′(z)

dz = N − P ,

2πi

f (z)

где

N = ∑nk -

число нулей f(z) с учетом их кратности,

P = ∑pk - число полюсов f(z) с

учетом их порядка.

Доказательство:

∫

f ′(z)

dz =

2πi ∑res

f ′(z)

= ∑res

f ′(z)

= ∑resa

f ′(z)

∑resb

f ′(z)

2πi Γ

f (z)

2πi

f (z)

первое слагаемое - вычет по всем полюсам, второе - по нулям функции f (z)

= −∑pk + ∑nk = N − P.

Ч.т.д.

Пример:

Найти логарифмический вычет функции

f (z) =

sin2 z

относительно контура

= 3 .

(z3 + 8)(z + 4)

z0 = 0 - нуль кратности 2.

z1,2,3 = 3−8 - простые полюса.

Другие нули и полюса f(z) не лежат внутри контура. Следовательно:

	1	∫			f ′(z)	dz = 2 − 3 = −1
	2πi	∫				dz = 2 − 3 = −1
			z	=3	f (z)
			z	=3	f (z)
Геометрический смысл теоремы о логарифмическом вычете
(принцип аргумента):
					1			Γ arg f (z) = N − P,

							2π
Γ arg f (z) - приращение аргумента								при обходе точкой z контура Г один раз в
положительном направлении.

Итак, логарифмический вычет равен числу полных оборотов вокруг нуля вектора w = f (z) , когда z описывает контур Г в положительном направлении и равен N – P. Отсюда, в частности, следует, что если f(z) регулярна внутри Г (т.е. P = 0), то она содержит столько нулей, сколько раз вектор w = f (z) проделает полный оборот вокруг начала координат, когда z пройдет весь контур Г.

Теорема Руше:

Пусть f(z) и g(z) регулярны в ограниченной односвязной области D и на ее границе ΓD , и пусть z ΓD f (z) > g(z) . Тогда f(z) и F(z) = g(z) + f (z) имеют в D одинаковое число нулей.

Следствие (Основная теорема алгебры):

Многочлен степени n Pn (z) = a0 zn + ...+ an−1z + an , a0 ≠ 0 имеет ровно n нулей (с учетом их кратности).

Пример:

Найти число нулей уравнения z11 − 7z6 + 3z −1 = 0 в кольце: 1≤ z ≤ 2 .

ТФКП (мат. анализ, часть 4), семестр 4, лекция 9 – 10, стр. 7 из 7

Решение:

≤ 1;

γ1 :

= 1

а) в круге

f (z) = −7z6

g(z) = z11 + 3z −1

f (z)

g(z)

≤ 1+ 3+1 = 5

f (z)

g(z)

= 7;

γ1

у f (z) + g(z) нулей столько же, сколько у f (z) = −7z6

= 6

≤ 2;

γ2 :

= 2

б) в круге

в) в кольце количество нулей N = N2 − N1 = 11− 6 = 5 . Ответ: 5 нулей.

ТФКП (мат. анализ, часть 4), семестр 4, лекция 11 – 12, стр. 1 из 7

ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА. СПЕЦИАЛЬНЫЕ ФУНКЦИИ.

Интегралы, зависящие от параметра.

1. Собственные интегралы от параметра.

Пусть f (x,α) непрерывна на прямоугольнике G и α [α1,α2 ] существует определенный (собственный) интеграл по переменной x [a,b] (см. рис. 1.1):

∫ f (x,α)dx ,

который является функцией параметра α , т.е.:

J(α) = ∫ f (x,α)dx .

a
Теорема 1.
Если f (x,α) непрерывна на G, то J(α)	непрерывна на
отрезке [α1,α2 ] .
Замечание:	рис. 1.1.

Условия теоремы 1 являются достаточными, но не являются необходимыми.

Пример:

1. Доказать, что J(α) = ∫sgn(x −α )dx непрерывна на множестве α .

			0
Решение:
		1, x >	0
				- разрывная.
Функция sgn x = 0, x = 0				- разрывная.

		−1, x < 0
Пусть α < 0 : sgn(x −α ) = 1, т.к. x [0,1] x −α > 0						1
Пусть α < 0 : sgn(x −α ) = 1, т.к. x [0,1] x −α > 0						J(α) = ∫dx = 1.
						0
Пусть		α >1:			sgn(x −α ) = −1 ,	т.к.

	1
x −α < 0 J(α) = ∫(−dx) = −1.
	0
Пусть 0 ≤ α ≤1		: J(α) =	α sgn(x −α )dx +		1 sgn(x −α )dx =
			∫		∫
			∫		∫
			0	<0	α
				<0

α1

∫(−dx)+ ∫dx = −α +1−α = 1− 2α.

0α

	−1,α > 1
Итак,		≤ α ≤ 1	- непрерывна (см. рис. 1.2).
Итак,	J(α) = 1− 2y, 0	≤ α ≤ 1	- непрерывна (см. рис. 1.2).
	1,α < 0

Хотя	интегрируемая функция разрывная, J(α) -			Рис. 1.2.

непрерывна!

<<< < Предыдущая 1 2 3 4 56 / 76 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.09.2019412.16 Кб13MapReduce.doc
#
10.05.201552.22 Кб213Marketing_testy_s_otvetami_1 (1).doc
#
10.05.2015175.62 Кб19Matan.doc
#
16.04.20195.07 Mб40matan.doc
#
01.05.2025262.7 Кб0matan.docx
#
10.05.20156.91 Mб25matan4_bel.pdf
#
01.03.20251.73 Mб0Matlab_МБС.doc
#
10.05.2015559.27 Кб74mat_analiz_tipovik.pdf
#
13.08.2019891.39 Кб44medicina-katastrof.doc
#
10.05.2015374.73 Кб15metod1k.pdf
#
01.03.2025400.9 Кб0Metoda_030.doc