Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

matan4_bel

.pdf

Скачиваний:

Добавлен:

10.05.2015

Размер:

6.91 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

ТФКП (мат. анализ часть 4) семестр 4, лекция 4 стр. 6 из 7

3. Функция Жуковского

w =

z +

Регулярна z,z ≠ 0

(проверьте!)

′

Производная w =

1−

(получите!)

′

z = ±1

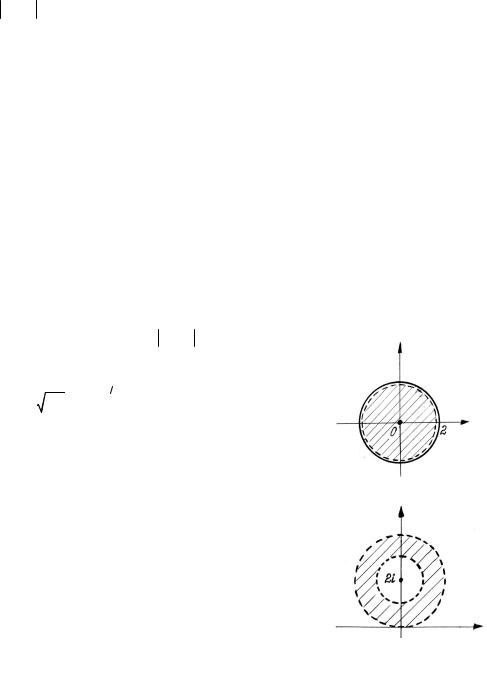
Конформное отображение для z ≠ ±1, т.к. w = 0

Задача для самостоятельного решения:

Доказать, что любая окружность, проходящая через точки z1 =1 и z2

= −1, делит всю

плоскость на две области однолистности функции Жуковского.

= r0

≠1 в эллипсы с полуосями

Функция Жуковского переводит окружности

a =

r0 +

; b =

−

и фокусами в z = ±1.

4. Тригонометрические и гиперболические функции.

sin z	eiz − e−iz		Регулярна	Периодическая T = 2π
		2i

cos z	eiz + e−iz		Регулярна	Периодическая T = 2π
	2

sh z		ez − e−z	Регулярна	Периодическая T = 2πi
	2

ch z		ez + e−z	Регулярна	Периодическая T = 2πi
	2

Отображения, осуществляемые этими функциями, являются композицией ранее изученных отображений.

Например, w = cos z - это композиция поворота на угол π , показательной функции и

функции Жуковского, т.е.

1)w1 = iz
2)w = ew1
2
3)w =	1		+	1
		w2
	2	w2
	2			w2

ТФКП (мат. анализ часть 4) семестр 4, лекция 4 стр. 7 из 7

Пример:

Найти образ полосы M = {z :0 < Re z < π} при отображении w = cos z

Полоса М перейдет в плоскость с двумя разрезами по действительной оси: (−∞,−1] и [1,+∞)

(см. рис. 4.1)

рис. 4.1.

ТФКП (мат. анализ часть 4) семестр 4, лекция 5, стр. 1 из 5

Интегрирование функций комплексного переменного.

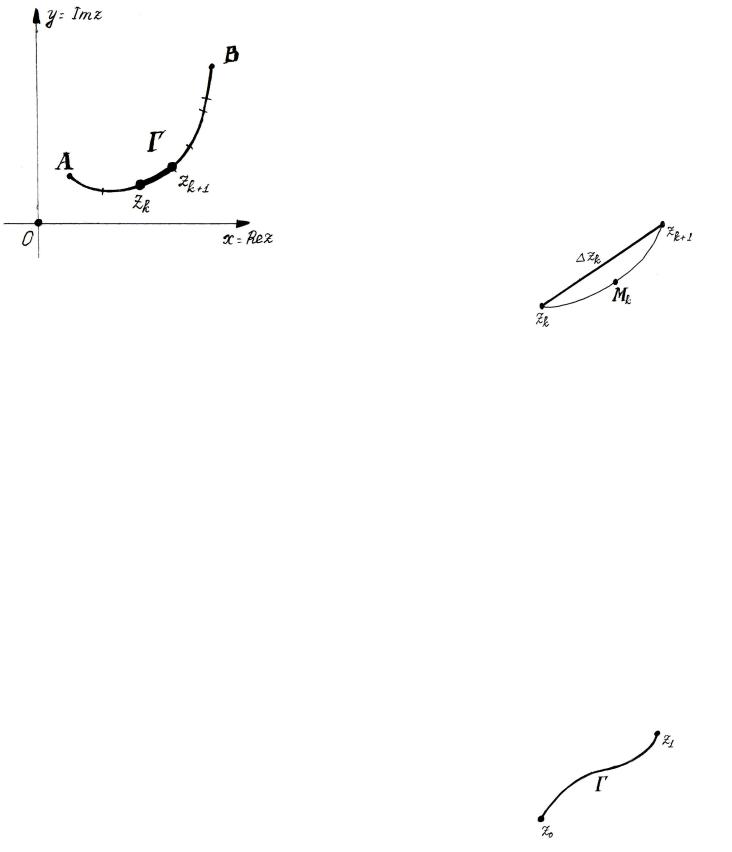
1. Определение интеграла по кривой в .

Пусть f(z) определена на . Γ – кусочногладкая кривая на комплексной плоскости, соединяющая точки А и В (без самопересечений) – см рис. 1.1. Разобьем ее на n дуг в направлении от А

	к В точками zk						и рассмотрим дугу, соединяющую
	zk		и zk+1 - см. рис. 1.2.
					Выберем		Mk	на	этой дуге
					Выберем		Mk	на	этой дуге	Mk (zk ; zk+1 );
	zk = zk+1 − zk ;						составим		интегральную сумму
	n
	∑ f (Mk ) zk .
	k=1
					Если			существует
						n
			lim	→0		∑ f (Mk )	zk	и он не
			lim			∑ f (Mk )	zk	и он не
рис. 1.1.	max		zk			k=1
		n→∞				k=1
		n→∞
	зависит от способа разбиения
	зависит от способа разбиения
и выбора точек Mk , то он называется интегралом f(z) по дуге
									AB и
обозначается ∫ f (z)dz .										рис. 1.2.
Γ

2. Связь с криволинейным интегралом II рода.

Пусть f (z) = u(x; y) + i v(x; y) z = x + i y;

z = x + i y; dz = dx + i dy;

∫ f (z)dz =∫(u + i v)(dx + i dy)= ∫(u dx + i v dx + i u dy − v dy)=

Γ Γ Γ

= ∫u dx − v dy + i ∫v dx + u dy

Γ	Γ
Re∫ f (z)dz	Im∫ f (z)dz
Γ	Γ

Re∫ f (z)dz , Im∫ f (z)dz - криволинейные интегралы II рода (см. материал II-го семестра).

ΓΓ

3. Основные свойства интеграла.

1) Теорема существования.

Если Γ - кусочно-гладкая дуга, f(z) – непрерывна на Γ , то существует ∫ f (z)dz .

Γ
2) ∫dz = z1 − z0 - см. рис. 3.1.	рис. 3.1.

3) Линейность:

∫[C1 f1(z) + C2 f2 (z)]dz = C1 ∫ f1(z)dz + C2 ∫ f2 (z)dz

Γ Γ Γ

4)Аддитивность:

∫f (z)dz = ∫ f (z)dz + ∫ f (z)dz

Γ=Γ1 Γ2

Γ1

Γ2

Γ= =

AC AB BC

(см. рис. 3.2)

5)Изменение направления интегрирования:

∫f (z)dz = − ∫ f (z)dz

Γ+	Γ−
	6) Оценка модуля:

Если f (z) ≤ M z Γ , то ∫ f (z)dz ≤ M l . где l – длина кривой Γ .

7) Теорема о среднем не верна!

ТФКП (мат. анализ часть 4) семестр 4, лекция 5, стр. 2 из 5

рис. 3.2.

4. Теорема Коши для односвязной области.

Определение односвязной области.

Область D называется односвязной, если любой замкнутый контур можно «стянуть» в любую ее точку. См. рис. 4.1. – здесь область D1 – односвязная, D2 и D3 – нет (D2 с выколотой точкой; D3 с выколотой точкой, «разрезом» и «дыркой»).

рис. 4.1.

Определение замкнутого контура.

Замкнутый контур – кусочно-гладкая замкнутая кривая без самопересечений, т.е. z(t1 ) ≠ z(t2 ), если t1 ≠ t2 (кроме концов).

То есть, исключаем линии такого вида - см. рис. 4.2:

рис. 4.2.

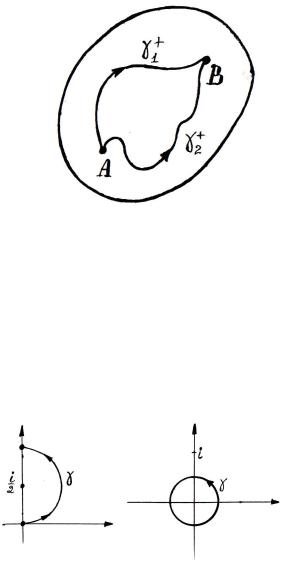
Теорема.

Если f(z) – регулярна в D, а D – односвязна, то интеграл по

любому замкнутому контуру γ D равен нулю:	∫ f (z)dz = 0
	γ

(см. рис. 4.3).
Доказательство:		рис. 4.3.
Для облегчения доказательства примем такие дополнительные		рис. 4.3.
Для облегчения доказательства примем такие дополнительные
условия: u = Re f (z); v = Im f (z) - непрерывные и дифференцируемые, и

ТФКП (мат. анализ часть 4) семестр 4, лекция 5, стр. 3 из 5

имеют непрерывные частные производные.

			в силу доп. условий
				∫		∂Q		∂P
∫(u + i v)(dx + i dy)= ∫udx − v dy + i ∫vdx + u dy = для этих интегралов				∫	Pdx + Qdy = ∫∫	∂x	−	dxdy
γ	γ	γ		γ	S	∂x		∂y
			верна формула Грина
			верна формула Грина

∂v

∂u

∂v

−

dxdy + i

−

dxdy

∫∫D

∂x

∂y

∫∫D

∂x

∂y

= −

∫∫D

∂v +

∂u dxdy + i

∫∫D

∂u −

∂v dxdy

∂x

∂y

∂x

∂y



но в силу регулярности f (z)
					=
= выполнены условия Коши-Римана:					=
	∂u	∂v	∂u	∂v
	∂u	∂v	∂u	∂v
	∂x	= ∂y	и ∂y = − ∂x
	∂x	= ∂y	и ∂y = − ∂x
= 0.

=0	=0
	Ч.т.д.
Следствие:

Пусть γ1 и γ2 - два контура с общим началом и концом без самопересечений, лежащие в односвязной области D (см. рис.

4.4), а	f(z) – регулярна в		D. Тогда:	∫ f (z)dz = ∫ f (z)dz . То		есть
				γ1	γ 2
интеграл от регулярной функции по контуру не зависит от
пути интегрирования, а зависит от начальной и конечной
точки. Действительно,
∫ f (z)dz + ∫ f (z)dz = 0 , т.к. γ1+			и γ2− образуют замкнутый контур.
γ +	γ −
1	2
Следовательно,
					B
∫ f (z)dz = − ∫ f (z)dz		∫ f (z)dz = ∫ f (z)dz = ∫ f (z)dz .				рис. .4.4.
γ +	γ −	γ +	γ +		A
1	2	1	2

Для регулярной функции в односвязной области верна формула Ньютона – Лейбница:

B
∫	f (z)dz = F(z)	B	= F(B) − F(A)	.
∫	f (z)dz = F(z)	A	= F(B) − F(A)	.
A

А, следовательно, интегралы от функций комплексного переменного в области их регулярности вычисляются методами действительного анализа.

Примеры:

3iz

∫(z2 + 3iz)dz = ∫(z2 + 3iz)dz =

(−1) = −

−

i = −

(см. рис. 4.5).

2) ∫

= 0; γ :

z − i

Контур γ области регулярности, следовательно, ∫= 0

рис. 4.5.

рис. 4.6.

(см. рис. 4.6.).

ТФКП (мат. анализ часть 4)

семестр 4, лекция 5,

стр. 4 из 5

3) ∫

;

γ :

z − i

= 1 (см. рис.4.7).

z − i

Теорема

Коши

неприменима,

т.к.

в точке

z0 = i

нарушается регулярность. Запишем

параметрическое уравнение этой окружности:

x − x0

= Rcost,

= 0

x = cost

= 1

= Rsint

y − y0

= 1

y = 1+ sint

z = x + i y = cost + i (1+ sint) = cost + i sint + i = ei t

+ i

(0 ≤ t ≤ 2π )

2π

d (ei t + i)

2π

dei t

2π

iei t dt

2π

∫

= ∫

= i ∫ dt = 2πi

i t

+ i − i

i t

z − i

рис. 4.7.

5. Теорема Коши для многосвязной области.

Теорема.

Если f(z) – регулярна в области D, ограниченной кривыми: Γ0 , Γ1, Γ2 , Γ3,…,Γk , то

∫ f (z)dz = 0, где Γ = Γ0 + Γ1 + Γ2 +…+ Γk

- полная граница области (см. рис. 5.1).

Доказательство:

Проведем

разрезы

γ1, γ2 ,…,γ k

будем

обходить

«общий» контур в таком порядке:

γ1+ , Γ1,γ1− , часть Γ0 , γ2+ , Γ2 , γ 2− , часть Γ0 ,…,γ k+ , Γk ,γk− , Γ0 .

Тогда

мы

обойдем ставшую односвязной область D, следовательно:

∫ +∫+ ∫ + ∫ + ∫ + ∫ +…+ ∫ + ∫ + ∫ + ∫ = 0 , но

γ +

−

γ +

−

∫ = − ∫, ∫ = − ∫, …, ∫ = − ∫

∫+ ∫ +…+ ∫ + ∫ = 0 ∫ f (z)dz = 0 .

γ +

γ −

γ +

−

γ +

γ −

Γ Γ

Ч.т.д.

Следствие:

рис. 5.1.

∫

= − ∑∫

i=1 Γ

Замечание:

Обход выбран так, что область остается слева (по Γ0 против часовой стрелки, по Γi (i =1, 2,…, k) - по часовой стрелке). Такой обход принято считать обходом в положительном направлении.

ТФКП (мат. анализ часть 4) семестр 4, лекция 5, стр. 5 из 5

6. Интегральные формулы Коши.

Теорема 1.

Функция f(z) – регулярна в замкнутой односвязной области, т.е. регулярна в любой ее точке, следовательно:

f (z0 ) =	1	∫		f (z)		dz ,	(*)

	2πi			z − z	0
		Γ	D

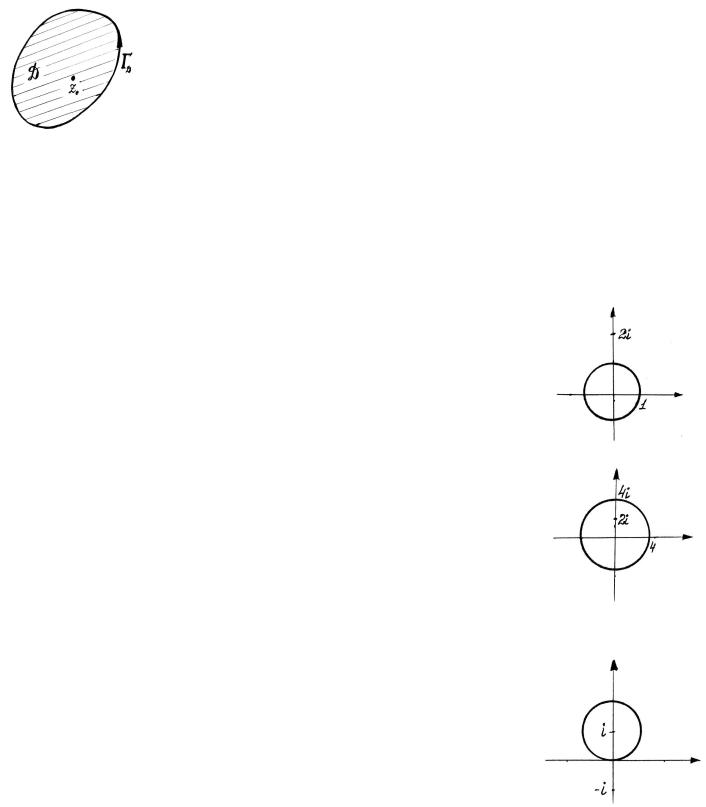
где z0 D - любая точка внутри области, ΓD - граница области D (см. рис. 6.1).

рис. 6.1.

Теорема 2.

Функция f(z) – регулярна в замкнутой односвязной области D (в том числе в точке z0 ), следовательно, существуют производные всех порядков в z0 и

f (n) (z0 ) =	n!	∫	f (z)	dz	(**)
			n+1
	2πi ΓD		(z − z0 )

Замечание:

Формула (*) называется интегральной формулой Коши для функции; формула

(**)– интегральной формулой Коши для производной.

Применение формул (*) и (**):

1) Вычислить ∫

dz = 0 (по теореме Коши для односвязной области)

z − 2i

см. рис. 6.2.

2) Вычислить

(*)

∫

dz = 2πi f (2i) = (здесь f (z) = z2 - регулярна) = 2πi (2i)2

= −8πi

z − 2i

рис. 6.2.

см. рис. 6.3.

3) Вычислить ∫

sin zdz

= 0 (по теореме Коши)

см. рис. 6.4.

z−i

(z + i)

4) Вычислить

sin zdz

2πi

∫

f ′′(−i) =

(здесь f (z) = sin z) =πi(sin z)′′

= πi(−sin(−i))= πisini =

z+i

(z + i)

z=−i

рис. 6.3.

= πi

ei i

− e−i i

= π

e−1 − e1

= −π sh1

Примечание:

Доказательство теоремы 1 можно прочесть в книге:

В.Д. Морозова «Теория функций комплексного переменного», М.: издво МГТУ им. Баумана, 2002 (Выпуск X в серии «Математика в техническом университете»), на стр. 164 – 165 (глава 5, пункт 5.5, теорема 5.8).

Доказательство теоремы 2 – там же, на стр. 170 (глава 5, пункт 5.6,

теорема 5.9).

рис. 6.4.

с показателем

обобщенный гармонический ряд

n=1

wn+1 = d , то при

n=1

d <1

∞

ряд ∑wn абсолютно сходится, а при

ТФКП (мат. анализ часть 4) семестр 4, лекция 6, стр. 1 из 5

Комплексные ряды.

1. Числовые ряды с комплексными членами.

Напомним некоторые понятия и факты, изучавшиеся в курсе рядов.

Последовательность комплексных чисел {zn} называется сходящейся, а число

z ее пределом (lim zn = z), если существуют конечные пределы			x = lim xn и
n→∞			n→∞
y = lim yn , где xn = Re zn , yn = Im zn
n→∞
	∞
Ряд с комплексными членами w1 + w2 + ...+ wn = ∑wn называется сходящимся,
	n=1
если последовательность {Sn}		n

	его частичных сумм сходится Sn	= ∑wk
		k=1

Комплексное число S = lim Sn называется суммой сходящегося числового ряда

n→∞

∞

с комплексными членами. Иногда пишут ∑wn → S .

n=1

∞

Ряд с комплексными членами ∑wn называется абсолютно сходящимся, если

n=1

∞

сходится ряд ∑

. В этом случае ряд ∑wn тоже сходится. Напомним, что

n=1

un + ivn

= un2 + vn2 > 0 .

∞

Ряд ∑

- числовой

знакоположительный ряд, следовательно, его

n=1

сходимость (расходимость) можно установить с помощью известных нам признаков Даламбера и Коши.

Теорема 1.

Если существует lim

n→∞

d >1 этот ряд расходится.

Теорема 2.

∞

Если существует lim n wn = c, то при c <1 ряд ∑wn абсолютно сходится, а при

n→∞

c >1 этот ряд расходится.

Примеры:

∞

ein

cosn +isin n

1) ∑

; wn

;

n=1

∞

cos2 n +sin2 n =

∑

=∑

−

n=1

∞

2 −i n2

2 −i

2) ∑

; wn

;

n=1

lim n

= lim

= 0 <1

n→∞

α = 2 >1 ряд (1) сходится абсолютно.

ряд (2) абсолютно сходится.

ТФКП (мат. анализ часть 4) семестр 4, лекция 6, стр. 2 из 5

2. Комплексные степенные ряды.

∞

Степенным рядом ранее мы называли ряд вида ∑Cn (z − z0 )n , где Cn и z0 -

n=0

комплексные числа, а z - комплексная переменная.

Те значения переменной z , при которых ряд сходится, образуют область сходимости.

Для любого степенного ряда существует круг с центром в точке z0 , внутри которого степенной ряд абсолютно сходится, а вне его – расходится.

Этот круг 0 ≤ z − z0 < R < +∞ называется кругом сходимости, а его радиус R - радиусом сходимости.

Для степенных рядов верна теорема Абеля (см. предыдущий семестр).

Верны также следующие два утверждения:

Теорема 1.

Во всех точках z внутри круга сходимости степенной ряд абсолютно

∞

сходится и его сумма S(z) = ∑Cn (z − z0 )n - регулярна.

n=0

Теорема 2.

Если степенной ряд абсолютно сходится в какой-либо точке границы круга, то он абсолютно сходится и на всей границе.

Рассмотрим теперь ряды по отрицательным степеням разности (z − z0 ):

∞	bn
∑				.
	(z − z		)n
n=1		0

Для рядов такого вида областью сходимости будет являться не внутренность, а внешность круга, т.е. множество вида z − z0 > r ≥ 0 .

Примеры:

Найти область сходимости степенного ряда

∞

1 n

1) ∑

zn ;

∑

;

lim n

= lim

< 1

< 2 (см. рис. 2.1)

n=1

n=1 2

n→∞

n→∞ 2

= 2 ∑n − расходится абсолютной сходимости на границе нет.

2) ∑(z − 2i)

+ ∑ n

+ 5

∞

(2) − ряд по всем целым

степеням (z − 2i)

n=0

2n (n

+1)

n=1 (z − 2i)n

рис. 2.1

+1)

wn+1

2n (n

I : lim

− 2i

lim

z − 2i

< 1

z − 2i

< 2

− область D

n→∞

n→∞ 2n+1(n + 2) 2

wn+1

(n +1)2 + 5

< 1

z − 2i

> 1

− область D

II : lim

lim

z − 2i

+ 5

z −

n→∞

n→∞ n2

D = DI

∩DII

= {z :1<

z − 2i

< 2}

(см. рис. 2.2)

рис. 2.2

ТФКП (мат. анализ часть 4) семестр 4, лекция 6, стр. 3 из 5

3. Ряды Тейлора и Лорана.

Функция f (z) , регулярная в круге z − z0 < R, 0 ≤ R < +∞ , раскладывается в ряд по

	∞
степеням (z − z0 )	вида: f (z) = ∑an (z − z0 )n . Этот ряд называется рядом Тейлора. В силу
	n=	0

существования у регулярной функции производных любого порядка, коэффициенты an определяются аналогично коэффициентам ряда Тейлора для действительных функций:

an = f (n) (z0 )

Это выражение для коэффициентов называется дифференциальным. В силу

интегральной формулы Коши для производной

f (n) (z0 ) =

∫

f (z)dz

можно получить

2πi

n+1

(z − z

)

интегральное выражение для коэффициентов:

∫

f (z)dz

∫

f (z)dz

, где γ :

z − z0

= r .

n+1

n! 2πi

(z − z

)

2πi

(z − z

)

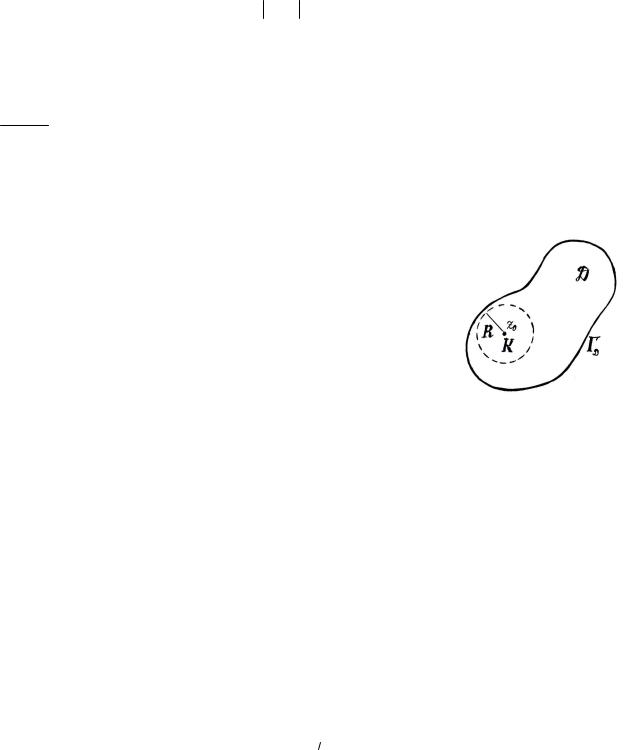
Если функция f (z)

регулярна в области D

(см. рис. 3.1), а точка

z0 D , то ряд Тейлора

этой

функции

f (z) сходится к ней внутри максимального

круга К с центром в z0 , лежащего в области D

∞

∑an (z − z0 )n → f (z)

в К . То есть радиус сходимости

n=0

R = min

z1 − z0

(ГD − граница области)

рис. 3.1

z1 ГD

f (z) , регулярная в кольце r <

z − z0

< R,

0 ≤ r < R < +∞ ,

Функция

∞

раскладывается в

ряд

по степеням

(z − z0 )

вида:

f (z) = ∑ an (z − z0 )n , где

n=−∞

an =

z−z∫

f (z)dz

, n = 0;±1;±2;...

2πi

=ρ (z − z0 )n+1

r<ρ<

Этот ряд называется рядом Лорана. Его можно представить в виде суммы

∞

−1

∞

двух рядов: ∑ an (z − z0 )n = ∑ an (z − z0 )n + ∑an (z − z0 )n

n=−∞

n=0

Первое слагаемое этой суммы называется главной частью ряда Лорана, а второе – правильной частью.

Ряды Тейлора и Лорана определяются единственным образом (докажите!)

Ряды Тейлора и Лорана можно почленно дифференцировать и

интегрировать (сформулируйте и докажите соответствующие теоремы).

Примеры:

Разложить в ряд по степеням z функции e3z ,

z3e1 z ,

z −

f1(z) = e3z

регулярна

во

всей

комплексной

плоскости (

< +∞) , следовательно,

раскладывается в ряд Тейлора, сходящийся к

f1(z)

при любом z :

f (n) (0)

, т.к. (e3z )(n)

= 3n e3z

∞

f1 (z) = e3z = ∑

zn = 1+ 32 +

27z

+...

n=0

<<< < Предыдущая 1 2 34 / 74 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.09.2019412.16 Кб13MapReduce.doc
#
10.05.201552.22 Кб213Marketing_testy_s_otvetami_1 (1).doc
#
10.05.2015175.62 Кб19Matan.doc
#
16.04.20195.07 Mб40matan.doc
#
01.05.2025262.7 Кб0matan.docx
#
10.05.20156.91 Mб25matan4_bel.pdf
#
01.03.20251.73 Mб0Matlab_МБС.doc
#
10.05.2015559.27 Кб74mat_analiz_tipovik.pdf
#
13.08.2019891.39 Кб43medicina-katastrof.doc
#
10.05.2015374.73 Кб15metod1k.pdf
#
01.03.2025400.9 Кб0Metoda_030.doc