Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

matan4_bel

.pdf

Скачиваний:

Добавлен:

10.05.2015

Размер:

6.91 Mб

Скачать

☆

1 / 71 2 3 4 5 6 7 > Следующая >>>

a = Rez; b = Im z .

соответственно

ТФКП (мат. анализ часть 4) семестр 4, лекция 1, стр. 1 из 10

Комплексные числа и функции.

1.Комплексные числа (повторение).

1.Основные определения.

Определение 1.

Комплексным числом (КЧ) называется упорядоченная пара действительных чисел:

(a;b) (a;b )

Определение 2.

Действительные числа а и b называются действительной (вещественной) и мнимой частью КЧ и обозначаются

Название «КЧ» было предложено Гауссом. Принято обозначать КЧ буквой z: z = (a;b) .

	2. Равенство КЧ.					z1 = (x1; y1 ); z2 = (x2 ; y2 )
	= z2	x	= x	Re z		= Rez
z1	= z2	1	2		1		2
		y1 = y2		Im z1 = Im z2

3. Действительные и чисто мнимые числа.

КЧ (1;0) называется действительной единицей.

КЧ (0;1) называется мнимой единицей. Мнимую единицу в математике обозначают буквой i. Это обозначение ввел Эйлер.

4. Сложение и умножение КЧ. z1 ± z2 = z = (x1 ± x2 ; y1 ± y2 )

z1 z2 = z = (x1x2 − y1 y2 ; y1x2 + x1 y2 )

Если z1 = z2 = i = (0;1)	z1 z2 = i i = (−1;0) = −1
Таким образом

				i2 = −1
5. Алгебраическая форма КЧ.
Любое КЧ можно представить в виде z = a(1;0) + b(0;1)

		z = a + bi	- алгебраическая форма		(1)
или z = Re z + iIm z . Подчеркнем еще раз: Re z и Im z - действительные числа.
Если a = 0	z = ib - чисто мнимое число.
Если b = 0	z = a - чисто действительное число.
Действительные и чисто мнимые числа – это подмножества множества КЧ.

r = z = OP

назовем

z = x + iy

ТФКП (мат. анализ часть 4) семестр 4, лекция 1, стр. 2 из 10

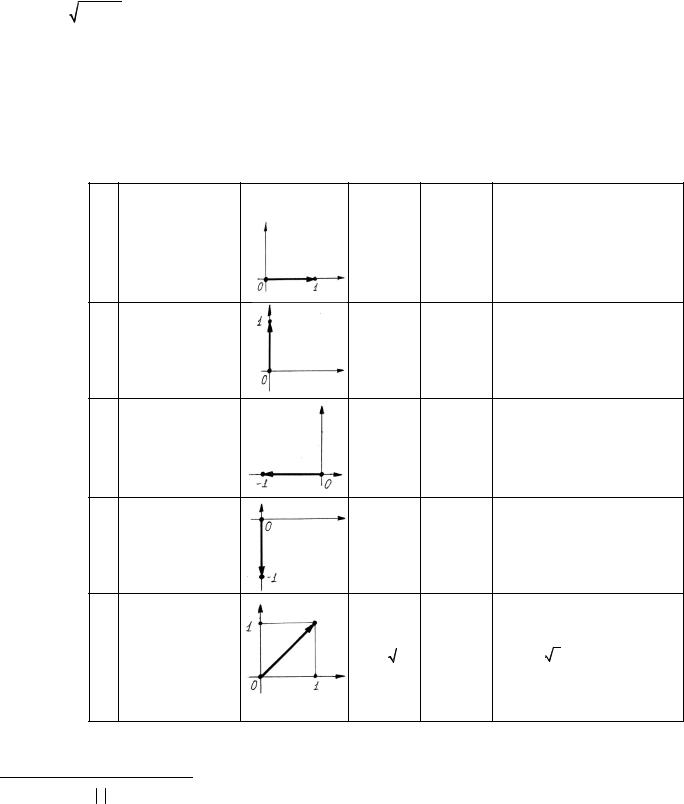
Примеры:

	Комплексное число					Алгебраическая форма	Действительная часть	Мнимая часть
1		1;0			)	z = 1	Re z =1	Im z = 0
		(
2		(	0;1			z = i	Re z = 0	Im z =1
					)
3			1;1			z =1+ i	Re z =1	Im z =1
		(		)
4		1;−1				z = 1− i	Re z = 1	Im z = −1
	(				)
5	(	0;			)	z = −i	Re z = 0	Im z = −1
				−1
6	(−2;3)					z = −2 + 3i	Re z = −2	Im z = 3

7	(3;−2)					z = 3− 2i	Re z = 3	Im z = −2

8	(a;b)					z = a + bi	Re z = a	Im z = b

9	(0;0)					z = 0	Re z = 0	Im z = 0

6. Геометрический смысл КЧ.

Каждой упорядоченной паре действительных чисел можно поставить в соответствие точку на плоскости с координатами, равными элементам этой пары. Пусть ось абсцисс (0х) – действительная ось, ось ординат (0у) – мнимая ось. Тогда каждому числу соответствует точка Р с координатами (x; y) - см. рис. 1.6.1.

Плоскость, на которой изображаются точками комплексные числа,

комплексной плоскостью. Обычно ее обозначают: . z

Примечание:
Числа вида	z = x	(y ≡ 0)	- действительные;
изображаются на действительной оси.
Числа вида	z = iy	(x ≡ 0)	- точками на мнимой

оси.

рис. 1.6.1. Геометрический смысл КЧ

7. Тригонометрическая форма КЧ.

Соединим начало координат с точкой Р, изображающей комплексное число z (см. рис. 1.7.1).

Определение 3.

Модулем (r) комплексного числа называется длина вектора OP :

Обозначим	ϕ	угол	между	положительным
направлением оси 0х и вектором OP .
Определение 4.					рис. 1.7.1.
Угол ϕ называется		главным значением аргумента			рис. 1.7.1.
Угол ϕ называется		главным значением аргумента

комплексного числа z ≠ 0 и обозначается ϕ = arg z . Очевидно, что 0 ≤ r < +∞ .

ТФКП (мат. анализ часть 4) семестр 4, лекция 1, стр. 3 из 10

Для ϕ однозначно не определяется область изменения. Можно выбирать в зависимости от задачи 0 ≤ϕ < 2π или −π < ϕ ≤ π .

Аргументом z называется Argz = arg z + 2π k, k .

Из соотношений в прямоугольном треугольнике следуют связи1:

x = rcosϕ				(2)
				(2)
y = rsinϕ
и наоборот:
r =
r =	x2 + y2
				(3)
		y		(3)
tgϕ =		y
tgϕ =
		x
Подставим связь (2) в формулу (1). Получим z = x + iy = rcosϕ + irsinϕ

			z = r(cosϕ + isinϕ)	(4)

Определение 5.

Формула (4) носит название тригонометрической формы комплексного числа.

Примеры:

	Алгебраическая	Изображение	r =		z	ϕ = arg z	Тригонометрическая

	форма						форма

1	z =1		z	=1		ϕ = 2π	z = cos2π + isin 2π

2	z = i	z	=1	ϕ = π	z = cosπ + isin π

				2	2	2

z = −1

ϕ = π

z = cosπ + isinπ

ϕ = −π

z = cos

− π

+ isin

−π

z = −i

ϕ =

3π

				ϕ = π	z =		cos π		+ isin π
5	z = 1+ i	z	= 2			2
				4				4	4

1 Если z ≡ 0 , то z = 0 , а arg z - не определен.

ТФКП (мат. анализ часть 4) семестр 4, лекция 1, стр. 4 из 10

2π

= 2

ϕ = −

2π

z = 2

cos

−

+ isin

−

z = −1−i 3

8. Показательная форма комплексного числа.

z = reiϕ

(5)

r = z ; ϕ = arg z

Возьмем два известных разложения:

cosϕ =1−

ϕ2

ϕ4

−

ϕ6

+ ...

sinϕ = ϕ −

ϕ3

ϕ5

−

ϕ7

+ ...

Умножим sinϕ на i и сложим:

ϕ2

ϕ4

ϕ6

iϕ3

iϕ5

iϕ7

cosϕ + isinϕ

1−

−

+ ...

iϕ −

−

+ ...

=1+ iϕ + (iϕ )2

+ (iϕ )3

+ (iϕ)4

+ (iϕ )5

+ (iϕ )6

+ ... = eiϕ

r(cosϕ + isinϕ ) = reiϕ

Это две разные формы записи одного и того же КЧ.

Определение 6.

Формула (5) носит название показательной формы комплексного числа.

Пример:

Рассмотрим число i3 +1. Запишем его всеми возможными способами.

z= (1;3) - по определению.

z=1+ i3 - алгебраическая форма;

z= 2 cos π + isin π - тригонометрическая форма;

3 3

πi

z = 2e 3 - показательная форма.

рис. 1.8.1. Геометрическое представление числа

i3 +1

9.Действия с комплексными числами, заданными в различных формах.

Сложение и вычитание

z1 ± z2 = (x1 + iy1 ) ± (x2 + iy2 ) = (x1 ± x2 ) + i(y1 ± y2 )

Умножение

z1 z2 = (x1 + iy1 ) (x2 + iy2 ) = x1x2 + i y1x2 + i y2 x1 + i2 y1 y2 = (x1x2 − y1 y2 ) + i(x1 y2 + x2 y1 )

или

z1 z2 = re1 iϕ1 r2eiϕ2 = rr1 2ei(ϕ1 +ϕ2 ) = rr1 2 (cos(ϕ1 +ϕ2 ) + isin(ϕ1 +ϕ2 ))

При умножении модули комплексных чисел перемножаются, а главные значения аргументов складываются.

Возведение в степень Из умножения в показательной форме следует:

ТФКП (мат. анализ часть 4) семестр 4, лекция 1, стр. 5 из 10

zn = z z ... z	= r r ... r ei(ϕ+ϕ +...+ϕ) = rneinϕ = rn (cosnϕ + isinnϕ )

n	n

		zn = rn (cosnϕ + isinnϕ)	(6)

Формула (6) – формула Муавра-Лапласа для возведения в степень.Операция сопряжения

Число z = x − iy называется сопряженным к числу z = x + iy . На плоскости они обозначаются векторами, симметричными относительно действительной оси:

(x; y)

(x;−y) - сопряженная пара

рис. 1.9.1. Обозначение сопряженной пары на плоскости

Свойства операции сопряжения: zz = (x + iy)(x − iy) = x2 + y2 = z 2

z + z = x + iy + x − iy = 2x = 2 Re z

Деление

												(x1 + iy1 )(x2 − iy2 )								= (x1x2 + y1 y2 ) + i(x2 y1 − x1 y2 )
	z1		= z1			z2			=			(x1 + iy1 )(x2 − iy2 )								= (x1x2 + y1 y2 ) + i(x2 y1 − x1 y2 )
												(x + iy			)(x − iy				)				+ y2
	z	2		z	2		z	2				(x + iy		2	)(x − iy			2	)			x2	+ y2
		2			2			2					2	2	2			2				2	2
или:
	z1		=	r1eiϕ1						=	r1		ei(ϕ1 −ϕ2 ) =			r1	(cos(ϕ −ϕ					)+ isin(ϕ −ϕ			))
			=	r eiϕ2						=			ei(ϕ1 −ϕ2 ) =				(cos(ϕ −ϕ					)+ isin(ϕ −ϕ			))
	z	2		r eiϕ2							r					r				1	2		1	2
		2	2								2				2

Извлечение корня – формула Муавра

ϕ + 2π k

iϕ +2π k

n z = n r cos

+ isin

= n r e

n , k = 0;1;...;n −1.

ϕ +2π k

(7)

				Доказательство:
Возведем обе части формулы (7) в степень n по формуле2 (6). Получим:
z = (n		)n ei	ϕ +2π k	n = rei(ϕ+2π k) = r(cos(ϕ + 2π k)+ isin(ϕ + 2π k))= 2(cosϕ + isinϕ ) z ≡ z
z = (n	r	)n ei	n
				Ч.т.д.

2 При извлечении корня n-ой степени получится ровно n чисел, лежащих на одной окружности R = nr и они делят

эту окружность на n дуг равной длины.

ТФКП (мат. анализ часть 4) семестр 4, лекция 1, стр. 6 из 10

Примеры:

1. Представить число, сопряженное с z =1+ i в тригонометрической форме и изобразить на плоскости.

z = 1+ i z = 1− i

ϕ = − π , r = 2 4

z = 2 (cos(−π4)+ isin(−π4))

2. В какой четверти лежит точка, соответствующая частному																																		1− i	?

																																		i − 2
	1− i							(1− i)(−2 − i)														−2 + 2i − i −1				−3+ i		3 1
				=																	=				=			= −		+		i
	i − 2			=			(−2 + i)(−2 − i)														=	5			=		5	= −	5	+	5	i				рис. 1.9.2.
Re z < 0;											Im z > 0											II четверть														для примера 1
Re z < 0;											Im z > 0											II четверть

3. Решить уравнение и изобразить решения на комплексной
плоскости: z4 + 4 = 0
		4														4								π + 2π k				π + 2π k
		4														4								π + 2π k				π + 2π k
	z		= −4												z =			−4 =					2 cos				+ isin						, k = 0,1,2,3.
	z		= −4												z =			−4 =					2 cos				+ isin						, k = 0,1,2,3.
																								4				4

											2					2
	z1 =										2		+ i			2			= z4			= −z3
					2
					2
									2					2
									2					2

													2				2
	z2 =									−			2		+ i		2				= z3 = −z4
						2
						2
												2				2
												2				2

													2				2
	z3 =								−				2		− i		2				= z2 = −z1
						2
						2
											2					2
											2					2

											2					2
			=								2		− i			2				= z1		= −z2														рис. 1.9.3.
	z4					2
	z4					2
									2					2																						для примера 3
									2					2																						для примера 3

2. Задание областей на комплексной плоскости.

Геометрический смысл модуля комплексного числа – расстояние до начала координат. Геометрический смысл модуля разности двух комплексных чисел – расстояние между точками, изображающими эти числа (см. рис. 2.1).

Отсюда следует, что окружность можно задать уравнением

z − z0

= R > 0

(8)

(см. рис. 2.2)

рис. 2.1. Геометрический смысл	рис.2.2.
модуля разности двух КЧ
модуля разности двух КЧ

ТФКП (мат. анализ часть 4) семестр 4, лекция 1, стр. 7 из 10

Примеры:

z= 1 - см. рис. 2.3

z−1 = 1 - см. рис. 2.4

z− i = 1 - см. рис. 2.5

z−1− i = 2 - см. рис. 2.6

z −1− i = 1 - см. рис. 2.7

рис. 2.3 рис. 2.4 рис. 2.5 рис. 2.6 рис. 2.7

Если вместо знака «=» в (8) поставить неравенство, то это геометрически будет соответствовать заданию следующих множеств:

z − z0		≤ R - круг (см. рис. 2.8)
z − z0		< R - открытый круг (см. рис. 2.9)

z − z0		> R - внешность открытого круга (см. рис. 2.10)

z − z0		≥ R - внешность круга (см. рис. 2.11)

рис. 2.8	рис. 2.9		рис. 2.10		рис. 2.11


Геометрический смысл равенства arg z = ϕ0		- луч .		(9)
(см. рис. 2.12)
Неравенства типа α ≤ arg z < β задают
сектор на плоскости (с границей, если
неравенство нестрогое, и без границы, если
строгое) – см. рис. 2.13.
Система неравенств	соответствует
пересечению множеств.

рис. 2.12

рис. 2.13

ТФКП (мат. анализ часть 4) семестр 4, лекция 1, стр. 8 из 10

	Пример:
1≤		z − i	≤ 2		− кольцо
1≤		z − i	≤ 2		− кольцо
				3π

D :	≤ arg z ≤				− сектор
0
0
				4

Все границы включены – см. рис. 2.14.

рис. 2.14

Более обширный обзор различных областей – на практических занятиях.

3. Расширенная комплексная плоскость.

Для нужд теории функций комплексного переменного, комплексную плоскость3 дополняют бесконечно удаленной точкой, соответствующей условному комплексному числу z = ∞ . Для наглядного изображения расширенной комплексной плоскости

= ∞ , проведем специальное геометрическое построение (см. рис. 3.1).

рис. 3.1

z ↔ z′ (взаимно-однозначное соответствие)

Условимся, что z = ∞ ↔ N . Тогда между точками сферы и точками - взаимно однозначное соответствие. Это соответствие называется стереографической проекцией.

Сфера S называется сферой Римана.

3 На действительной числовой прямой две бесконечно удаленных точки x → +∞; x → −∞ . На комплексной плоскости

– одна!

ТФКП (мат. анализ часть 4) семестр 4, лекция 1, стр. 9 из 10

4. Понятие функции комплексного переменного.

Если z D поставлено в соответствие одно (или несколько) чисел w G , то на D определена функция комплексного переменного w = f (z) - однозначная (или многозначная) – см. рис. 4.1.

рис. 4.1

Примеры:

w = z2 = (x + iy)2 - однозначная

w = 4z - многозначная

Значение функции представимо в виде

w = u + iv f (z) = u + iv , но z = x + iy f (x + iy)= u + iv u = u(x; y) = Re f (z) v = v(x; y)= Im f (z)

Определение 7.

Функции двух действительных переменных U (x; y);V (x; y) называются

действительной и мнимой частью функции w = f (z) .

Пример:

w = z2 = (x + iy)2 = x2 + 2xiy − y2 = (x2 − y2 )+ i(2xy)

(

)

= U

(

x; y

)

= x2 − y2

Im(z2 )= V (x; y) = 2xy

Основные классы функций комплексного переменного:

, где z – комплексная переменная; a,b .

линейная функция:

w = a z + b

Пример:

w = i z

дробно-линейная:

w =

a z + b

, где z – комплексная переменная; a,b,c,d .

c z + d

Пример:

w =

рациональная:

w = a0 zn + a1zn−1 +…+ an−1z + an

, где ai

Пример:

w= 8iz3 − 3z2 + (2 + i)z − 3

4)дробно-рациональная: w = Pn (z) , где P(z),Q(z) - многочлены вида 3.

Qn (z)

ТФКП (мат. анализ часть 4) семестр 4, лекция 1, стр. 10 из 10

Пример:

w =

z2 + 4

5) показательная:

w = ez

∞

Определения: ez

= ex+iy = ex(cos y+isin y)

или ez = ∑

< +∞ .

n=1

Пример:

= e0 cos

π + isin

e2 i

= e0+ 2 i

= i

6) тригонометрические функции:

w = sin z = eiz − e−iz

w = cos z = eiz + e−iz

∞

2n+1

или w = sin z = ∑(−1)n

;

< +∞

n=0

(2n +1)!

∞

или w = cos z = ∑(−1)n

;

< +∞

n=0

(2n)!

w = tg z =	sin z	;	w = ctg z =	1

	cos z			tg z

гиперболические функции:

ez − e−z

ez + e−z

sh z

ch z

sh z =

; ch z =

; th z =

;

cth z =

ch z

sh z

th z

= ln

+ i(arg z + 2π k); k = 0,±1,±2,…

логарифмическая функция:

ln z = ln

+ i arg z

ln z = ln z + i arg z - главное значение логарифма.

Пример:

ln(−1) = ln −1 + i(arg(−1)) = ln1+ i(π + 2π k) = πi(2k +1); k = 0,±1,±2,…

9) сложная показательно-степенная функция: w = f (z) = [u(z)]v(z) = elnuv = ev(z)lnu(z)

Пример:

i i

+2π k

−

+2π k

ii = eln i

= eilni = ei(ln

+iargi) = e

= e

; k = 0,

±1,±2,…

1 / 71 2 3 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.09.2019412.16 Кб15MapReduce.doc
#
10.05.201552.22 Кб213Marketing_testy_s_otvetami_1 (1).doc
#
10.05.2015175.62 Кб23Matan.doc
#
16.04.20195.07 Mб41matan.doc
#
01.05.2025262.7 Кб1matan.docx
#
10.05.20156.91 Mб26matan4_bel.pdf
#
01.03.20251.73 Mб2Matlab_МБС.doc
#
01.07.20251.1 Mб0matlog.doc
#
10.05.2015559.27 Кб77mat_analiz_tipovik.pdf
#
13.08.2019891.39 Кб48medicina-katastrof.doc
#
01.07.202517.27 Mб1Mekh_obor_Romanov_81-760_761.doc