Лабораторные работы по физике-во
.pdf
3
где – a ускорение грузов, I-момент инерции блока, R-радиус блока, g – ускорение свободного падения. Исключая из этих выраже-
ний T1 и T2 и учитывая, что I = mблR2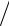 
2, выражаем ускорение g:
g = |
2M + m + mбл 2 a |
(2) |
|
m |
|
Ускорение a определяем, зная путь S, пройденный каждым грузом, и время t движения грузов:
a = |
2S |
. |
(3) |
|
|||
|
t2 |
|
|
В результате ускорение свободного падения g определяется по формуле:
g = |
2S |
|
2M + m + mбл |
2 |
(4) |
t 2 |
m |
|
Порядок выполнения работы
1.Перекинуть через блок 2 нить с двумя грузами 3 и 4 и убедиться, что система находится в положении безразличного равновесия.
2.Установить кронштейн с фотодатчиком 6 в нижней части шкалы вертикальной стойки, а фотодатчик расположить таким образом, чтобы правый груз при движении вниз проходил в центре рабочего окна фотодатчика (за нижнее положение груза берется риска шкалы, соответствующая риске на корпусе фотодатчика, находящейся на продолжении оптической оси фотодатчика 7, которую пересекает движущийся груз).
3.Положить на правый груз перегрузок 5.
4.Установить правый груз в крайнем верхнем положении.
5.При помощи визира на шкале вертикальной стойки зафиксировать положение нижней плоскости груза 4 с перегрузком 5.
6.Нажать на кнопку «ПУСК» электронного блока 8. Происходит растормаживание электромагнита, правый груз начинает опускаться, а таймер электронного блока начинает отсчет времени. При пересечении правым грузом оптической оси фотодатчи-
4
ка(7) отсчет времени прекратится. Записать показания таймера с дисплея электронного блока измерения времени t движения грузов. Повторить измерения 3-4 раза.
7.Определить по шкале пройденный грузом путь S, как расстояние от положения визира до оптической оси фотодатчика 7 (плоскость кронштейна, окрашенная в красный цвет).
8.Повторить измерения по пп. 1 – 6 с теми же грузами М и с другим перегрузком m.
9.Повторить измерения по пп. 1 – 8, изменив массу M грузов 3 и 4.
10.Повторить измерения по пп. 1–9, изменив высоту подъема груза M c перегрузком m.
11.Для каждого из измеренных значений ускорения a определить значение ускорение свободного падения g.
Значения масс M и m выбирать по согласованию с преподавателем.
Обработка результатов измерений
1. Результаты измерений должны быть оформлены в виде следующей таблицы:
Таблица 1
№ п/п |
S, см |
M, г |
m, г |
t,с |
tср , с |
a, м/с2 |
g, м/с2 |
1 |
S1 |
M1 |
m1 |
t1 |
tср1 |
a1 |
g1 |
2 |
|
|
|
t2 |
|
|
|
3 |
|
|
|
t3 |
tср2 |
|
|
4 |
|
|
m2 |
t1 |
a2 |
g2 |
|
5 |
|
|
|
t2 |
|
|
|
6 |
|
|
|
t3 |
tср3 |
|
|
7 |
|
M2 |
m1 |
t1 |
a3 |
g3 |
|
8 |
|
|
|
t2 |
|
|
|
9 |
|
|
|
t3 |
tср4 |
|
|
10 |
|
|
m2 |
t1 |
a4 |
g4 |
|
11 |
|
|
|
t2 |
|
|
|
12 |
|
|
|
t3 |
tср5 |
|
|
13 |
S2 |
M1 |
m1 |
t1 |
a5 |
g5 |
|
14 |
|
|
|
t2 |
|
|
|
15 |
|
|
|
t3 |
tср6 |
|
|
16 |
|
|
m2 |
t1 |
a6 |
g6 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
|
|
|
|
t2 |
|
|
|
18 |
|
|
|
|
t3 |
tср7 |
|
|
19 |
|
M2 |
m1 |
|
t1 |
a7 |
g7 |
|
20 |
|
|
|
|
t2 |
|
|
|
21 |
|
|
|
|
t3 |
tср8 |
|
|
22 |
|
|
m2 |
|
t1 |
a8 |
g8 |
|
23 |
|
|
|
|
t2 |
|
|
|
24 |
|
|
|
|
t3 |
|
|
|
2.Из данных таблицы определяют среднее значение ускорения свободного падения gср.
3.Для одного из опытов рассчитывают случайную погрешность измерения времени по формуле:
t =αn, p |
∑( ti )2 |
(5) |
|
n(n −1) |
|||
|
|
(для числа измерений времени n=3 с доверительной вероятностью p=0,7 коэффициент αn, p =1,39)
4. Оценивают относительную погрешность определения g по формуле:
Е = |
g |
= |
S |
+ |
2 t |
+ |
m |
+ |
m1 |
+ |
mбл |
(6) |
g |
S |
|
m |
m |
||||||||
|
|
|
t |
|
m |
|
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|
бл |
|
5. Записывают результат измерений |
|
|
|
|||||||||
|
|
|
|
|
g = gср ± |
|
g |
|
|
(7) |
||
6. Сравнивают полученное значение g с табличным.
Лабораторная работа 1.25 ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ С
ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА.
Ф.А. Шаталов, В.А. Фотиев
Цель работы: исследование законов вращательного движения на примере маятника Обербека.
Задание: из отношения времени падения грузов, создающих вращательные моменты для движения маятника Обербека, найти среднюю величину силы трения, приложенную к оси системы, и убедиться в выполнении основного уравнения динамики вращательного движения.
Подготовка к выполнению лабораторной работы: изучить по-
нятия момента инерции точки и твердого тела, момента силы, уравнение вращательного движения твердого тела относительно неподвижной оси, изучить описание установки и уметь выводить расчетнуюформулу дляопределения средней величинысилытрения.
Библиографический список
1.Савельев И.В. Курс общей физики. - М.: Наука, 1987, т.1, гл. V, параграфы 36 - 43.
Контрольные вопросы
1.Дайте определение момента инерции материальной точки и твердого тела относительно некоторой оси вращения.
2.Дайте определение момента силы относительно некоторой оси.
3.Выведете основное уравнение вращательного движения.
4.Как определить направление вектора угловой скорости вращения относительно некоторой оси?
5.Опишите устройство маятника Обербека.
6.Чему равен суммарный момент сил, действующих на ось вращения маятника Обербека?
7.Выведите расчетную формулу для определения силы трения, действующей на ось маятника Обербека.
8.Оцените погрешность определения силы трения.
2
Описание аппаратуры и метода измерений
Вращение твердого тела постоянной массы вокруг неподвижной оси описывается основным уравнением динамики вращательного движения. При постоянном значении момента инерции тела I
относительно оси вращения это уравнение запишется в виде |
|
M = Iβ , |
(1) |
где M - суммарный момент внешних сил, приложенных к телу, относительно оси вращения, β - угловое ускорение вращения.
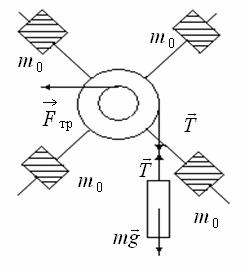
Изучение динамики вращательного движения производится на установке, схематически изображенной на рис. 1 и получившей название маятника Обербека.
Четыре спицы укреплены на горизонтально расположенном цилиндре под прямым углом друг к другу. Вдоль спиц могут перемещаться грузы одинаковой массы m0 , закрепляемые с помо-
щью винтов на произвольном расстоянии от оси вращения, что дает возможность изменять момент инерции всей системы.
Рис.1
При одинаковом расстоянии грузов от оси вращения система находится в состоянии безразличного равновесия. С цилиндром жестко соединен шкив, на который намотана нить. К свободному концу нити может быть прикреплен груз массы m. Цилиндр и шкив насажены на общую горизонтальную ось, что по-
3
зволяет всей системе вращаться вокруг нее.
При опускании груза m вращающий момент силы натяжения нити равен
M T =TR , |
(2) |
где R – радиус шкива; T – сила натяжения нити.
Величину Т можно определить из второго закона Ньютона
ma = mg −T , |
(3) |
где а- линейное ускорение груза. Так как поступательное движение груза m носит равноускоренный характер, то
h = |
at2 |
, |
(4) |
|
2 |
||||
|
|
|
где h – расстояние, на которое опускается груз за время t. Пользуясь уравнениями (2), (3) и (4), найдем величину мо-
мента силы натяжения нити
MT = mR(g − 2h t 2 ) . |
(5) |
К цилиндру при его вращении приложен со стороны оси момент силы трения, который равен
M тр = Fтр r , |
(6) |
где Fтр - средняя величина силы трения; r - радиус оси вращения.
Таким образом, если в качестве груза использовать гирю массы m, то суммарный момент сил, приложенных к маятнику, согласно выражениям (5) и (6), равен
M = M |
|
− M |
|
= mR(g − |
2h |
) |
− F |
|
r . |
(7) |
T |
тр |
|
|
|||||||
|
|
|
t2 |
тр |
|
|
||||
|
|
|
|
|
|
|
|
|
||
При этом учтено, что моменты сил T и Fтр |
направлены в проти- |
|||||||||
воположные стороны (см. рис. 1)
При последовательном использовании в качестве грузов двух гирь массами m1 и m2 , отношение суммарных моментов сил, которое обозначим через n1 , будет равно
n |
= |
M1 |
= |
m1R(g − 2h t12 ) − Fтр r |
. |
(8) |
|||
|
|
||||||||
1 |
|
M |
2 |
|
m R(g − 2h t2 ) − F r |
|
|||
|
|
|
|
2 |
2 |
тр |
|
||
Здесь t1 и t2 - промежутки времени, за которые грузы массами m1
4
и m2 проходят одно и то же расстояние h.
Обычно в опытах ускорение a (см. формулу (4)), с которым движутся грузы, мало по сравнению с ускорением свободного падения g, т.е. выполняется неравенстве a << g . Поэтому форму-
лу (8) можно упростить и привести к виду
|
|
m g |
|
R |
|
− F |
|
||
|
|
r |
|
||||||
n1 = |
1 |
|
|
|
тр |
|
|||
|
|
|
|
|
|
. |
(9) |
||
|
|
|
R |
|
|
||||
|
|
m g |
|
|
− F |
|
|||
|
|
|
|
|
|||||
|
2 |
|
r |
|
|
тр |
|
||
|
|
|
|
|
|
|
|
|
|
Угловое ускорение вращения маятника Обербека β связано |
|||||||||
с линейным ускорением движущегося |
груза а соотношением |
||||||||
a = βR , откуда с учетом (4) |
|
2h |
|
|
|||||
|
β = |
|
(10) |
||||||
|
Rt2 |
||||||||
|
|
|
|
||||||
Обозначим через n отношение угловых ускорений, с которыми происходит вращение маятника (рис. 1) при использовании
в качестве грузов гирь массами |
m1 и |
m2 . Если грузы проходят |
||||
одинаковые расстояния, то согласно (10) |
||||||
|
β |
|
t2 |
|
||
n = |
1 |
|
= |
2 |
. |
(11) |
β2 |
|
|||||
|
|
t12 |
|
|||
Если момент инерции системы, на которую последовательно действуют моменты силы M1 и M 2 , остается неизменным, то в соответствии с (1) угловые ускорения β1 и β2 относятся друг к другу так жe, как моменты внешних сил, т.е.
β1 |
= |
M1 |
, |
(12) |
|
β2 |
M 2 |
||||
|
|
|
откуда следует, что в этом случае n1 = n .
Пользуясь формулой (9) можно найти среднюю величину силы трения
F |
= |
m1 −m2n |
g R . |
(13) |
|
||||
тр |
|
1−n |
r |
|
|
|
|
5
Порядок выполнения работы
1.Размещают грузы на спицах на одинаковом расстоянии от оси таким образом, чтобы система находилась в состоянии безразличного равновесия - крестовина без подвешенного на нити груза не должна вращаться независимо от ее начального положения.
2.Наматывают нить на шкив, укрепляют на ней груз m1 и измеряют расстояние от нижней плоскости груза до пола. (груз m1 > 150 г).
3.Определяют 5 раз время прохождения грузом m1 заданного расстояния.
4.Повторяют опыты 2 и 3 с грузом m2 > m1 .
5.С помощью штангенциркуля измеряют радиусы шкива R, на который намотана нить, и радиус оси r.
Обработка результатов измерений
1. Результаты должны быть оформлены в виде таблицы :
N 1 |
2 |
3 4 |
5 |
Среднее |
Случайная |
Погреш- |
|
ность |
|||||||
|
|
|
|
значение |
погрешность |
||
|
|
|
|
прибора |
t1
t2
t1
t2
2. Длякаждогоизгрузовопределяютсреднеезначение t1cp и t2cp и рассчитываютслучайныепогрешности t1cp и t2cp .
3.Рассчитывают отношение угловых ускорений n по фор-
муле (11).
4.Рассчитывают среднюю величину силы трения Fтр по
формуле (13). Если грузы, раскручивающие маятник, помещаются в чашечку, при расчетах необходимо учитывать суммарный вес гири и чашечки.
6
5. Определяют абсолютные погрешности измерений n и Fтр соответственно по формулам n = En и Fтр = EF Fтр, где
E = |
2 t1 |
+ |
2 t2 |
, EF = E + |
m1 + |
m2 + |
g |
+ |
R + |
r . |
|
|
g |
||||||||
|
t1cp |
t2cp |
m1 |
m2 |
|
R |
r |
|||
6. Записывают полученное |
значение силы |
|
трения в ви- |
|||||||
деFтр ± |
Fтр, производя округление величины Fтр |
с учетом абсо- |
||||||||
лютной погрешности измерений.