
Лабораторные работы по физике-во
.pdfЛабораторная работа № 1.85 ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ
С ПОМОЩЬЮ ОБОРОТНОГО МАЯТНИКА.
Е.В. Жданова
Цель работы: изучить закономерности движения физического маятника и с помощью оборотного маятника определить ускорение свободного падения.
Задание: экспериментально исследовать зависимости периода малых колебаний оборотного маятника в прямом и обратном положениях от координаты подвижного груза. Определить координату подвижного груза, при котором периоды колебаний маятника в обоих положениях одинаковы. Рассчитать ускорение свободного падения. Оценить погрешность проведённых измерений.
Подготовка к выполнению лабораторной работы: ознако-
миться с методикой определения ускорения свободного падения с помощью оборотного маятника и используемой измерительной аппаратурой. Ответить на контрольные вопросы.
Библиографический список
1.Савельев И.В. Курс общей физики, том1, §54, - М.: Наука, 1987.
2.Сивухин Д.В. Общий курс физики. т. I. Механика, §41, - М.:
Наука, 1989.
Контрольные вопросы
1.Дайте определение физического маятника.
2.Выведите формулу для периода колебаний физического маятника.
3.Какие колебания физического маятника являются изохронными?
4.Что называется приведенной длиной физического маятника и как она связана с моментом инерции физического маятника?
5.Сформулируйте теорему Штейнера.
6.Что такое сопряжённые точки?
7.Что называют центром качания?
2
8.Как с помощью оборотного маятника определить ускорение свободного падения?
9.Как зависит величина g от широты местности?
10.Как влияют на точность эксперимента колебания температуры, сила трения, амплитуда колебания маятника?
Описание аппаратуры и метода измерений
Оборотный маятник является частным случаем физического маятника, поэтому рассмотрим сначала колебания физического маятника около некоторой оси.
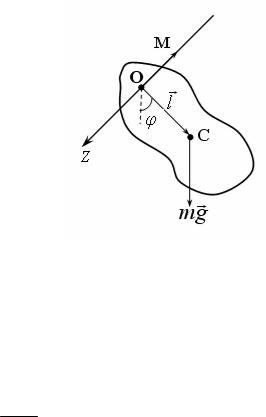
Физическим маятником называется любое твердое тело, которое под действием силы тяжести может совершать свободные колебания вокруг неподвижной точки О, лежащей выше его центра масс С (рис. 1).
Рис. 1 |
|
Уравнение движения маятника записывается в виде: |
(1) |
M = Iε |
где M - момент всех сил, действующих на маятник, относительно оси вращения, I - момент инерции маятника относительно оси
вращения, ε = d 2ϕ - угловое ускорение, ϕ - угол отклонения ма- dt 2
ятника от положения равновесия, t – время.
В том случае, если маятник совершает несколько десятков колебаний без заметного затухания, моментом силы трения в пер-

3
вом приближении можно пренебречь и считать, что при отклонении маятника от положения равновесия возникает вращательный момент силы тяжести, стремящийся уменьшить угол отклонения маятника. Тогда уравнение движения маятника примет вид:
I |
d 2ϕ |
= −mglinϕ, |
(2) |
|
dt 2 |
||||
|
|
|
где l – расстояние между точкой подвеса и центром масс. В случае малых колебаний угол ϕ - мал, и можно положить sinϕ ≈ϕ :
I |
d 2ϕ |
= −mglϕ . |
(3) |
||
dt |
2 |
||||
|
|
|
|||
Разделив обе части равенства (3) на I, |
после преобразований |
||||
получим дифференциальное уравнение гармонических колебаний физического маятника:
|
|
ϕ′′+ |
mgl |
ϕ = 0 , |
(4) |
|
|
mgl |
I |
||||
где |
=ω02 - квадрат циклической частоты колебаний физиче- |
|||||
I |
||||||
|
|
|
|
|
||
ского маятника. Следовательно, период малых колебаний физического маятника определяется формулой
T = |
2π = 2π |
I |
(5) |
|
ω0 |
mgl |
|
В частности, для математического маятника, масса которого сосредоточена в одной точке (центре инерции), имеем IМ = ml2.
Тогда из равенства (5) получаем
TM = 2π l g . |
(6) |
Для любого физического маятника существует такое понятие, как приведенная длина L - это длина такого математического маятника, период колебаний которого равен периоду колебаний физического, т.е.
T |
= 2π L =T = 2π |
I , |
(7) |
M |
g |
mgl |
|
|
|
где L= I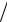 ml - приведенная длина физического маятника.
ml - приведенная длина физического маятника.
Точку O', отстоящую от точки подвеса O маятника на расстоя-
4
ние приведённой длины L= I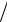 ml , называют центром качания физи-
ml , называют центром качания физи-
ческого маятника. Можно доказать, что точка подвеса и центр качания обратимы, т.е. при качании маятника вокруг точки О' период колебания должен быть таким же, как и при качании вокруг точки О. Т.е. если маятник подвесить за центр качания О', то его период не изменится, и прежняя точка подвеса О сделается новым центром качания. Такие точки подвеса, относительно которых период колебаний маятника является одинаковым, называются взаимными или сопряжёнными. Из формулы (5) следует, что период колебаний физического маятника не зависит ни от фазы, ни от амплитуды колебаний, что справедливо только для колебаний, подчиняющихся уравнению (3), т.е. для малых колебаний. Если период колебаний не зависит от амплитуды, то такие колебания называются изохронными. Колебания маятника приближённо изохронны, когда угловая амплитуда колебаний непревышает нескольких градусов.
По теореме Штейнера момент инерции маятника I относительно произвольной оси можно выразить как
I = Ic + ml2 , |
(8) |
где Ic - момент инерции маятника относительно параллельной оси, проходящей через центр масс С. При этом
T = 2π |
I |
c |
+ ml2 |
(9) |
|
mgl |
|||
|
|
|
|
Представляет интерес анализ зависимости периода Т колебаний физического маятника от величины l. В предельном случае больших значений l соотношение (9) переходит в (6), т.е. получаем математический маятник
T (l) |l→∞ = 2π l g . |
(9.1) |
При малых l маятник близок к положению безразличного равновесия. В этом случае из соотношения (8) получаем
T (l) | = 2π Ic . |
(9.2) |
l →0  mgl
mgl
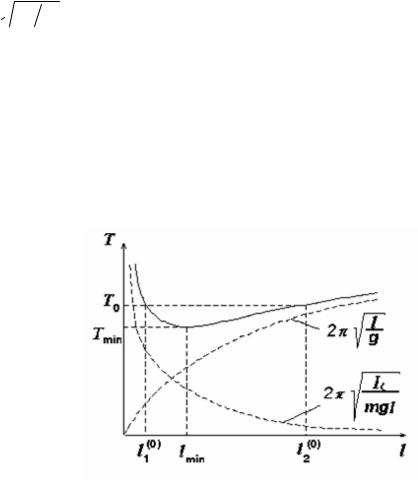
Примерный вид графика зависимости Т(l) представлен на рис. 2. Асимптотическое поведение функции при l→∞ и l→0 описывается выражениями (9.1) и (9.2). Можно показать, что при
5
lmin =  Ic m функция Т (l) имеет минимум.
Ic m функция Т (l) имеет минимум.
Рассмотрим возможность определения с помощью физического маятника ускорения свободного падения g. Точное измерение периода колебаний любого физического маятника позволяет в принципе определить ускорение свободного падения g в любой точке земного шара. Входящую в формулу (9) величину Ic, которую трудно найти из опыта, можно исключить, измеряя период колебаний при двух разных значениях l.
Рис. 2. Примерный вид графика зависимости Т(l)
Записав равенство (9) для l1 и l2, получим систему уравне-
ний
|
2 |
= 4π |
|
2 |
(Ic |
2 |
), |
|
||
mgl1T1 |
|
|
+ ml1 |
(9.3) |
||||||
|
2 |
|
|
|
2 |
|
2 |
|
||
|
= 4π |
(Ic |
|
|
||||||
mgl2T2 |
|
+ ml2 ). |
|
|||||||
Отсюда находим: |
|
|
l2 |
−l2 |
|
|
|
|
||
g = 4π |
2 |
|
|
|
|
(10) |
||||
|
|
1 |
|
|
2 |
|
|
|
||
|
T 2l |
−T 2l |
2 |
|
|
|||||
|
|
1 |
1 |
|
|
2 |
|
|
|
|
На практике трудно точно определить положение центра масс маятника, т.е. измерить l1 и l2 . Эту трудность можно обойти, если взять такие расстояния l1(0) и l2(0), чтобы соответствующие периоды были равны (см. рис. 2.), т.е. выполнялось условие T1(0) =T2(0) =T0 . Тогда, полагая l1(0) ≠ l2(0) , из равенства (10) полу-
чаем
6
|
|
g = |
4π 2 |
[l (0) |
+l (0) ]. |
(10.1) |
|
|
|
T 2 |
|||||
|
|
|
|
1 |
2 |
|
|
|
|
|
0 |
|
|
|
|
При этом, если оси расположены по разные стороны центра |
|||||||
масс, то сумма |
l (0) |
+l (0) |
есть просто расстояние l0 |
между осями, |
|||
|
1 |
2 |
|
|
|
|
|
которое легко измерить с высокой точностью.
Итак, если наблюдается равенство периодов колебаний физического маятника относительно двух осей, находящихся по обе стороны центра масс и на разном расстоянии от него, то величину g можно найти из соотношения
g = 4π 2 |
l0 |
, |
(10.2) |
|
|||
T 2 |
|
|
|
0 |
|
|
|
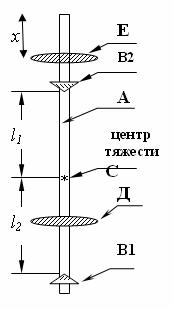
где l0 – расстояние между осями; T0 – общий период колебаний. В данной работе используется оборотный маятник, изобра-
женный на рис. 3. На металлическом стержне А, на котором нанесена сантиметровая шкала, жестко закреплены опорные призмы В1 и В2, рёбра которых могут служить осями колебаний маятника при прямом и обратном способах подвеса. В рабочем положении призмы устанавливаются в V -образные опоры штатива. Груз Д, положение которого в процессе измерений не изменяется, находится между опорными призмами.
Рис. 3
7
Второй груз Е, находящийся на конце стержня (не между призмами), может перемещаться по стержню А и закрепляться в нужном положении. Расстояние между призмами равно l=l1+l2. Положение фиксированного груза Д подобрано так, чтобы с помощью подвижного груза Е можно было бы добиться равенства периодов колебаний T1 и T2 маятника в прямом (осью является В1) и обратном положениях (ось - В2) при l1(0) ≠ l2(0) . Смещение
центра масс, необходимое для изменения расстояний l1 и l2, обеспечивается перемещением массивного груза Е, находящегося у конца стержня. Для более точного измерения величины
T1(0) =T2(0) =T0 в работе исследуется зависимость T1 и T2 от коор-
динаты х подвижного груза Е, которая отсчитывается от конца стержня по миллиметровой шкале, нанесённой на стержень А.
Поскольку расстояние l между осями фиксировано, то при смещении груза Е изменится положение центра масс маятника, и, следовательно, изменятся расстояния от центра масс до соот-
ветствующих точек подвеса (призм В1 и В2) l1′ и l2′, но сумма
этих расстояний останется прежней: |
l ′ +l |
2 |
′ = l +l |
2 |
= l . Если, к |
|
1 |
1 |
|
примеру, расстояние l1 увеличится, а l2, соответственно, уменьшится, то как видно из рис. 2, увеличение l1 и уменьшение l2 приведет к уменьшению периодов колебаний T1 и T2, и наоборот, уменьшение l1 и соответствующее увеличение l2 приведёт к увеличению периодов колебаний в прямом и обратном положениях. Однако, при достаточной асимметрии в расположении центра масс зависимость T(x) в обратном положении маятника будет более крутой, чем в прямом.
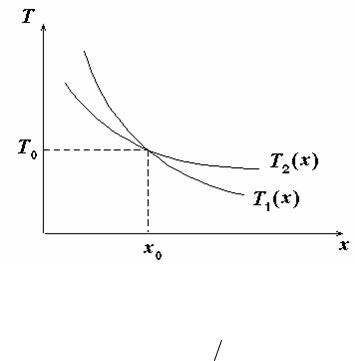
Таким образом, графики зависимостей T1(x) и T2(x) для прямого и обратного положений маятника будут иметь вид, изображенный на рис. 4. В результате значение T0 можно найти как ординату точки пересечения соответствующих кривых.
8
Рис. 4
Период колебаний маятника можно определить по формуле
T = t N , |
(11) |
где t – время, за которое совершается полное число колебаний N. При повторных измерениях удобно регистрировать время t одного и того же числа колебаний N. Тогда нет необходимости сразу переходить к величине Т. Практически удобнее исследовать зависимости t(x) для прямого и обратного положений маятника. Точка пересече-
ния соответствующих графиков даст величину t0 = t1(0) = t2(0) . Тогда
с учетом выражений (11), (10.2) получаем для расчета ускорения свободногопадениясоотношение
|
2 |
|
|
N |
2 |
|
|
g = 4π |
l0 |
|
|
(12) |
|||
|
|
||||||
|
|
|
. |
||||
|
|
|
t0 |
|
|
||
Порядок выполнения работы
1.При подготовке к выполнению работы следует установить стержень строго вертикально. Нижний конец стержня должен свободно проходить между окнами фотодатчика. Установить маятник так, чтобы подвижный груз находился на расстоянии 2 см от конца стержня. Ось маятника – ребро призмы В1.
2.Внимание! При работе с маятником следует соблюдать осторожность и убедиться, что ребро призмы, служащей осью подвеса, находится в углублении V-образной опоры. Амплитуда
9
колебаний должна составлять не более 10 градусов.
3.Измерить время t1 для N = 10–15 полных колебаний маятника. Запуск и остановка секундомера осуществляется фотоэлектрическим датчиком. При нажатии на клавишу “ПУСК“ начинается отсчет времени от момента прохождения маятником положения равновесия. При нажатии клавиши “СТОП” секундомер фиксирует длительность t целого числа колебаний на момент ближайшего во времени прохождения маятником положения равновесия. Число колебаний определяется специальным индикатором. Занести в таблицу 1 значения t, N и координаты x груза.
Повторить измерение времени t1 при неизменном числе колебаний и при данном значении х не менее трёх раз.
4.Перевернуть маятник (ось маятника – призма В2)и, повторив задание п. 2., определить время t2.
5.Повторить опыт при пяти - шести различных значениях x, перемещая груз из одного крайнего положения в другое.
6.Измерить расстояние l между ребрами призмы, служа-
щими осями подвеса маятника, и оценить его погрешность l.
Занести в таблицу 2 значения l и ность определения времени ∆tпр.
№ |
|
Положение х подвижного груза, см |
|
Количество колебаний N |
|
t1, |
|
t1ср |
|
∆t12 |
|
∆t1с |
|
|
|
|
|
|
|||||||
|
|
|
|
с |
|
с |
|
с2 |
|
л с |
||
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l, а также приборную погреш-
Таблица 1
∆t1 |
|
t2 с |
|
t2ср |
|
∆t22 |
|
∆t2с |
|
∆t2 |
|
|
|
|
|
||||||
с |
|
|
|
с |
|
с2 |
|
л с |
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10
4
5
6
Данные установки |
Таблица 2 |
||
∆tпр, с |
|
||
Расстояние между осями подвеса l, м |
∆l , м |
|
|
|
|
|
|
|
|
|
|
Обработка результатов измерений
1. Определить среднее значение времени N колебаний при различных положениях маятника и координатах х подвижного груза и квадраты отклонений отдельных измерений от среднего
значения |
t 2 |
= |
|
t |
ср |
−t |
i |
|
2 |
. Результаты расчётов занести в таблицу 1. |
|
|
|||||||||
|
i |
|
|
|
|
|
|
|
2. Рассчитать случайную погрешность измерения времени по формуле:
|
n |
|
|
∑( ti )2 |
|
tсл =αn, p |
i=1 |
, |
|
n(n −1) |
|
где αn, p =1, 4 (n=3, p=0,7).
3. Погрешностьизмерениявремени t определитьпоформуле
t = 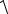 ( tсл)2 +( tпр)2
( tсл)2 +( tпр)2
изаписать в таблицу 1.
4.Построить графики зависимостей t1(x) и t2(x) для прямого
иобратного положений маятника. Вследствие погрешностей измерений, экспериментальные точки на графике t (x) могут не находиться на плавной кривой, предсказываемой теорией (см.
