
Краткий курс математического анализа. Том 1
.pdf
§ 6. Предел и непрерывность функций |
107 |
||||
П р и м е р 4. Пусть |
|
1, |
если |
x > 0, |
|
sign x def= |
|
||||
0, |
если |
x = 0, |
|
||
|
− |
если |
x < 0. |
|
|
|
|
1, |
|
||
Тогда (рис. 59 и рис. 60) предел lim |sign x| функции |sign x| по всей ее
x→0
области задания, т. е. по всей числовой прямой (или, что равносильно,
по любой окрестности U (0) точки x0 = 0), не существует, а предел этой |
||||||
|
|
|
|
|
|
◦ |
функции по проколотой окрестности U (0) точки x0 = 0 существует |
||||||
и равен 1: |
lim |
sign x |
| |
= 1. |
||
x |
0 |
| |
|
|
||
|
→ |
|
|
|
|
|
|
◦ |
|
|
|
|
◦ |
|
x U (x) |
|
|
|
||
Действительно, для любой последовательности xn U (0), n = |
||||||
= 1, 2, ..., |
lim xn |
= 0, имеем f (xn) = 1, а поэтому lim f (xn) = 1. Это |
||||
n→∞ |
lim |
|
|
n→∞ |
||
означает, что |
f (x) = 1, т. е. что предел по проколотой окрест- |
|||||
|
|
x→0 |
|
|
|
|
|
|
|
◦ |
|
|
|
|
x U (0) |
|
|
|
||
ности существует и равен 1. Если же xn = 1/n, xn = 0, n = 1, 2, ..., то |
||||||||||||||
lim |
x |
= lim x |
= 0, |
и |
f (x |
n |
) = 1, f (x |
n |
) = 0. |
|
lim f (x ) = 1, |
|||
n→∞ |
n |
n→∞ n |
|
|
|
|
|
Поэтому n→∞ |
n |
|||||
а |
lim f (x ) = 0. |
Это означает, что предел |
lim f (x) |
по всей окрест- |
||||||||||
n→∞ |
n |
x→0 |
||||||||||||
ности U (0) не существует. |
|
|
|
|
x U (0) |
|
|
|||||||
З а м е ч а н и е 2. Пусть заданы последовательность {xn} и функция ϕ: N → N. Введем обозначение ϕ(k) = nk и рассмотрим последовательность {xnk }. Иначе говоря, из значений последовательности {xn} образуем новую последовательность {xnk }, в которой порядок членов может не совпадать с их порядком в исходной последовательности. Таким образом, последовательность {xnk } не является, вообще говоря, подпоследовательностью последовательности {xn}.
В этих обозначениях справедливо следующее утверждение.
Л е м м а 1. Если существует конечный или бесконечный предел
nlim xn = a и |
klim nk = ∞, то klim xnk = a. |
|
→∞ |
→∞ |
→∞ |
Действительно, из условия |
lim xn = a следует, что для любо- |
|
|
|
n→∞ |
го ε > 0 существует такой номер n0, что для всех номеров n > n0

108 Гл. 1. Дифференциальное исчисление функций одной переменной
выполняется включение xn U (a, ε), а из условия lim nk = ∞, — что
k→∞
для n0 существует такой номер k0, что для всех k > k0 выполняется неравенство nk > n0 и, следовательно, включение xnk U (a, ε). Это
и означает, что lim xnk = a.
k→∞
Из леммы 1 следует, что понятие предела последовательности является частным случаем понятия предела функции.
Действительно, пусть предел последовательности {xn} равен a: |
|
nlim xn = a. Рассмотрим функцию f (n) = xn, n N. В силу лем- |
|
→∞ |
|
мы 1 для любой последовательности вида {xnk }, nk N, klim nk = ∞, |
|
имеем lim xnk |
→∞ |
= a, т. е. lim f (nk ) = a. Согласно определению 1 это |
|
k→∞ |
k→∞ |
и означает, что |
lim f (n) = a. |
n→∞
6.2. Определение непрерывности функции. При рассмотрении предела функции f (x), x X, в точке x0 случай, когда x0 X, представляет особый интерес — он приводит к понятию непрерывной
функции.
Если x0 X и существует предел lim f (x), то он равен f (x0):
lim f (x) = f (x0). |
(6.8) |
x→x0 |
|
В самом деле, поскольку x0 X, то в качестве последовательности |
||||
xn X, n = 1, 2, ..., nlim xn = x0, в этом случае можно взять стацио- |
||||
|
|
→∞ |
= x0, n = 1, 2, ... Для нее имеем |
|
нарную последовательность xn |
|
|||
|
|
lim f (xn) = |
lim f (x0) = f (x0). |
(6.9) |
|
|
n→∞ |
n→∞ |
|
Если |
существует предел lim f (x), то, согласно его определе- |
|||
нию, |
для |
x→x0 |
|
|
любой последовательности xn X, n = 1, 2, ..., для ко- |
||||
торой |
lim xn = x0, существует предел последовательности |
f (xn), |
||
|
n→∞ |
|
|
|
n = 1, 2, ..., и все пределы таких последовательностей равны между |
||||
собой. Поэтому из равенства (6.9) следует выполнение условия (6.8). О п р е д е л е н и е 5. Если
lim f (x) = f (x0),
x→x0
то функция f (x) называется непрерывной в точке x0. |
|
|
||||||||||
Согласно сказанному выше функция f (x) непрерывна в точке x0 |
||||||||||||
тогда и только тогда, когда существует предел (по множеству X) |
||||||||||||
lim f (x) |
и |
x |
0 |
X. |
Например, функция |
f (x) = |
2x2 + x − 1 |
является |
||||
x x0 |
|
|
|
x |
− |
1 |
||||||
→ |
|
|
|
|
|
|
|
|
|
|
|
|
непрерывной в точке x = |
0 (как и во всякой другой точке x = 1), ибо, |
|||||||||||
как это было показано в п. 6.1, |
|
|
|
|
|
|||||||
|
|
|
|
|
lim |
2x2 + x − 1 |
= 1 = f (0). |
|
|
|
|
|
|
|
|
|
|
x→0 |
x − 1 |
|
|
|
|
|
|
§ 6. Предел и непрерывность функций |
109 |
Функция же |
sin |
1 |
, |
если |
x = 0, |
|
|
|
f (x) = |
|
|
||||||
x |
|
|
||||||
|
0, |
|
|
если |
x = 0, |
|
|
|
не является непрерывной в точке x = 0, так как предел lim sin |
1 |
не |
||||||
x |
||||||||
существует. |
|
|
|
|
0 |
|
||
|
|
|
|
x→ |
|
|
||
6.3. Второе определение предела |
функции. Существует |
|||||||
другое определение предела функций, в котором используется понятие окрестности, оно называется определением по Коши.
О п р е д е л е н и е 6. Точку a называют пределом функции f (x), x X, при x → x0 (или, что то же самое, в точке x0) и пишут
lim f (x) = a, если для любой окрестности U (a) точки a существует
x→x0
такая окрестность U (x0) точки x0, что
f (X ∩ U (x0)) U (a).
Используя логические символы, это определение можно записать в следующем виде:
lim f (x) = a def U (a) U (x0) :
или, что равносильно,
lim f (x) = a def U (a) U (x0) x X ∩ U (x0): f (x) U (a) (6.10)
(в подобных символических записях двоеточие читается как «имеет место»).
Вспоминая определения окрестностей, эти определения для соот-
ветствующих |
конкретных случаев можно |
перефразировать в терминах неравенств. |
|
Рассмотрим важный случай, когда x0 и a — |
|
действительные числа. |
|
Число a называется пределом функ- |
|
ции f (x), x X, в точке x0 R, если |
|
для любого ε > 0 существует такое δ > 0, |
|
что для всех x, удовлетворяющих условию |
|
|x − x0| < δ, |
x X, выполняется неравен- |
ство |
|f (x) − a| < ε. |
|
|
Это определение действительно равносильно определению (6.10) в случае, если x0 R и a R, так как условие |x − x0| < δ равносильно
условию
x U (x0) = U (x0, δ),
а условие |f (x) − a| < ε — условию
f (x) U (a) = U (a, ε)
(рис. 61).

110Гл. 1. Дифференциальное исчисление функций одной переменной
Всимволической форме для рассматриваемого случая определение предела функции имеет вид
lim |
f (x) = a def |
ε > 0 |
δ > 0 |
x |
X, x |
x |
0 |
| |
< δ : |
f (x) |
− |
a |
< ε. |
x x0 |
|
|
|
|
| − |
|
|
| |
| |
|
|||
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Вчастности, если функция f непрерывна в точке x0 X R и a =
=f (x0) (в этом случае x0 и a являются числами), то определение непрерывности в символической записи имеет вид
lim f (x) = f (x0)
x→x0
ε > 0 δ > 0 x X, |x − x0| < δ : |f (x) − f (x0)| < ε.
В качестве примера бесконечных пределов рассмотрим определение предела lim f (x) = −∞:
|
x→+∞ |
|
|
|
|
|
1 |
|
|
1 |
|
|
lim |
f (x) = |
|
def |
ε > 0 |
δ > 0 |
x |
X, x > |
: f (x) < |
|
. |
||
−∞ |
δ |
− |
|
|||||||||
x + |
|
|
|
|
|
|
ε |
|||||
→ ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
Те о р е м а 1. Определения 1 и 6 предела функции в точке прикосновения множества задания функции равносильны.
Пусть функция f задана на множестве X и x0 — точка прикос-
новения этого множества. Предположим сначала, что lim f (x) = a
x→x0
в смысле определения 1, и покажем, что тогда число a является и пределом функции в смысле определения 6. Допустим, что это не так, т. е. (см. (6.10)), что существует такая окрестность U (a), что для любой окрестности U (x0) найдется такая точка x X ∩ U (x0), что f (x) U (a), или, в символической записи,
U (a) U (x0) x X ∩ U (x0) : f (x) U (a). |
(6.11) |
В частности, указанные точки x найдутся в каждой окрестности
U (x0, 1/n), n = 1, 2, ..., точки x0. Обозначим эти точки xn, т. е. |
|
xn X ∩ U (x0, 1/n), |
(6.12) |
f (xn) U (a). |
(6.13) |
Из условия (6.12) следует (см. пример в п. 5.3), что |
|
lim xn = x0. |
(6.14) |
n→∞ |
|
Поскольку a = lim f (x) в смысле определения 1, то из выполнения
x→x0
условия (6.14) следует, что lim f (xn) = a. Следовательно, для любой
n→∞
окрестности U (a), в частности, и для окрестности U (a), указанной в условии (6.13), существует такой номер n0, что для всех n > n0 выполняется включение
f (xn) U (a), |
(6.15) |
§ 6. Предел и непрерывность функций |
111 |
что противоречит условию (6.13). В одну сторону утверждение теоремы доказано.
Пусть теперь a = lim f (x) в смысле определения 6 предела функ-
x→x0 |
|
ции f : X → R, x0 — точка прикосновения множества X и xn → x0, |
|
xn X, n = 1, 2, ... Покажем, что nlim f (xn) = a. Зададим произволь- |
|
→∞ |
|
но окрестность U (a) точки a и выберем для нее окрестность U (x0) |
|
точки x0, удовлетворяющую условию (6.10). Для окрестности U (x0) |
|
в силу условия lim xn = x0 существует такой номер n0, |
что для |
n→∞ |
|
всех n > n0 выполняется включение xn U (x0), а так как xn X, |
|
n = 1, 2, ..., то при n > n0 будем иметь xn X ∩ U (x0). Следовательно, |
|
в силу (6.10) при n > n0 имеет место включение f (xn) U (a), т. е. |
|
lim f (xn) = a. |
|
n→∞ |
|
Это и означает, что lim f (x) = a в смысле определения 1. |
|
x→x0 |
|
6.4. Условие существования предела функции. |
Согласно |
определению предела функции (п. 6.1) для того, чтобы существовал
предел lim f (x) функции f (x), x X, нужно, чтобы для любых
x→x0
последовательностей xn → x0, xn X, n = 1, 2, ..., существовали пре-
делы lim f (xn) и они были равны между собой. Покажем, что второе
n→∞
условие вытекает из первого. То есть, не предполагая равенство этих пределов, а предполагая только их существование, можно доказать их равенство, а следовательно, и существование предела функции. Точнее, докажем следующее утверждение.
Л е м м а 2. Для того чтобы функция f (x), x X, имела конечный или (определенного знака) бесконечный предел в точке x0, являющейся конечной или бесконечно удаленной точкой прикосновения множества X, необходимо и достаточно, чтобы для любой последовательности xn → x0, xn X, n = 1, 2, ..., последовательность соответствующих значений {f (xn)} функции f имела предел конечный или соответственно (определенного знака) бесконечный.
Необходимость сформулированного условия для существования
lim |
f (x) содержится в |
самом определении предела |
функции |
x→x0 |
(6.4)), в котором |
утверждается существование |
пределов |
(см. |
lim f (xn) для всех указанных в условиях леммы последовательно-
n→∞
стей {xn}.
Докажем достаточность этого условия для существования предела
функции. Пусть xk → x0, xk → x0, xk X, xk X, k = 1, 2, ..., и су- |
||||||
ществуют пределы |
lim |
f (x ), |
lim f (x ). |
Покажем, что |
||
k→∞ |
k |
k→∞ |
k |
|
||
|
|
|
|
|
||
|
xk , если |
n = 2k |
|
1, |
|
|
xn = xk , |
если |
n = 2k,− |
|
k = 1, 2, ... |
||

112 Гл. 1. Дифференциальное исчисление функций одной переменной
Тогда lim xn = x0 и xn X, n = 1, 2, ... Согласно условиям леммы
n→∞
существуют пределы
lim f (xn), |
lim f (xn), |
lim f (xn), |
n→∞ |
n→∞ |
n→∞ |
причем {f (xn)} и {f (xn)} являются подпоследовательностями после-
довательности {f (xn)}.
Поскольку из существования у последовательности предела (конечного или бесконечного) следует существование того же предела у любой ее подпоследовательности, то будем иметь
lim f (xn) = |
lim f (xn) = lim f (xn). |
|
n→∞ |
n→∞ |
n→∞ |
Таким образом, пределы последовательностей {f (xn)}, где xn → → x0, xn X, n = 1, 2, ..., не зависят от выбора указанных после-
довательностей {xn}. Обозначив общее значение пределов последова-
тельностей {f (xn)} через a, получим lim f (x) = a.
x→x0
6.5. Предел функции по объединению множеств.
Л е м м а 3. Пусть функция f задана на объединении X1 X2 множеств X1 и X2, а x0 является точкой их прикосновения. Тогда если при x → x0 функция f имеет равные пределы по множествам X1 и X2, то она имеет тот же предел и по их объединению.
Если
lim f (x) = lim f (x) = a,
x→x0 |
x→x0 |
x X1 |
x X2 |
то для любой окрестности U (a) точки a существует такая окрестность |
|
U (x0) точки x0, что образы ее пересечений X1 ∩ U (x0) и X2 ∩ U (x0) |
|
с множествами X1 и X2 содержатся |
в окрестности U (a), а тогда |
и образ их объединения (X1 X2) ∩ U |
(x0) также содержится в U (a). |
Это и означает, что
lim f (x) = a.
x→x0 x X1 X2
6.6. Односторонние пределы и односторонняя непрерывность. Введем обозначения: для любого числового множества X и любой точки x0 расширенной числовой прямой R положим
def |
|
def |
|
|
X+(x0) = {x X : x x0}, |
X−(x0) = |
{x X : x x0}. |
||
Если x0 X, то |
x0 X+, x0 X−, а если |
x0 X, то x0 |
X+, |
|
x0 X−. Очевидно, если x0 = +∞, то X+(x0) = , а если x0 |
= −∞, |
|||
то X−(x0) = . |
|
|
|
|
В случае когда множество X+(x0) (соответственно множество |
||||
X−(x0)) непусто, условие, что x0 |
является его точкой прикоснове- |
|||
ния, равносильно |
тому, что x0 = inf X+(x0) (соответственно x0 = |
|||
= sup X−(x0)). |
|
|
|
|

§ 6. Предел и непрерывность функций |
113 |
О п р е д е л е н и е 7. Пусть задана функция f (x), x X и x0 R. Точка a называется пределом функции f слева при x → x0 (соответст-
венно справа), если она является пределом при x → x0 функции f по множеству X−(x0) (соответственно по множеству X+(x0)), т. е. если
lim f (x) = a (соответственно |
lim f (x) = a). |
x→x0 |
x→x0 |
x X−(x0) |
x X+(x0) |
В силу этого определения предел lim f (x) причисляется к пре-
x→+∞
делам слева, а lim f (x) — к пределам справа.
x→−∞
Иначе говоря, предел функции f слева в точке x0 — это предел в этой точке сужения функции f на множество X+(x0), а предел справа — это предел сужения f на множество X−(x0).
Для пределов справа и слева сужения функции f на множество X \ {x0}, т. е. для случая, когда предел берется по множеству, не содержащему точку x0, имеются специальные обозначения: для пре-
дела слева |
f (x |
0 |
lim |
|
f (x), |
а для предела справа |
f (x |
|
+ 0) |
||||||||||
|
0 − ) и x |
x0 |
|
0 |
|
|
0 |
|
|||||||||||
lim |
|
|
→ |
− |
|
|
|
0 |
вместо |
0 |
+ |
0 |
и |
0 |
− |
0 |
|
|
0 |
и x x0+0 f (x). При этом в случае x0 = |
|
|
|
|
|
пишут + |
|||||||||||||
→ |
|
|
|
|
|
|
|
|
|
= −∞) вместо +∞ − 0 |
|||||||||
и −0, а в случае x0 = +∞ (соответственно x0 |
|||||||||||||||||||
(−∞ + 0) пишут просто +∞ (соответственно −∞).
Если множества X−(x0) \ {x0}, X+(x0) \ {x0} не пусты, x0 является
их точкой прикосновения и существует предел |
lim f (x) по множе- |
|
|
|
x→x0 |
ству X, то он называется также двусторонним пределом. |
||
П р и м е р 1. Для функции y = sign x (см. рис. 59) имеем |
||
lim |
1, |
1 |
x +0 sign x = |
xlim0 sign x = |
− . |
→ |
→− |
|
Те о р е м а 2. Если функция f (x) задана на множестве X, x0 R,
X+(x0) = , X−(x0) = , sup X−(x0) = inf X+(x0) = x0, то для того, чтобы у функции f существовал предел lim f (x), необходи-
x→x0
мо и достаточно, чтобы в точке x0 существовали пределы слева и справа и они были равны (общее значение этих пределов является двусторонним пределом функции f в точке x0).
Если у функции f существует предел в точке x0, то тот же предел существует у этой функции при x → x0 и по любому подмножеству E X, для которого точка x0 является его точкой прикосновения, в частности по множествам X−(x0) и X+(x0). Обратно, если у функции f существуют равные пределы по множествам X−(x0) и X+(x0), то по лемме 3 у нее существует тот же предел и по их объединению, т. е. по множеству X = X−(x0) X+(x0).
114Гл. 1. Дифференциальное исчисление функций одной переменной
Оп р е д е л е н и е 8. Функция f (x), x X, называется непрерывной слева (справа) в точке x0 X, если
lim f (x) = f (x0) (соответственно |
lim |
f (x) = f (x0)). |
x→x0 |
x→x0 |
|
x X−(x0) |
x X+(x0) |
|
Из теоремы 2 следует, что если функция f |
непрерывна слева |
|
и справа в точке x0, то она непрерывна в этой точке (напомним, что непрерывность функции f в точке x0  означает, что в x0 существует предел функции f по множеству, содержаще-
означает, что в x0 существует предел функции f по множеству, содержаще-
му эту точку: |
lim f (x) = f (x0), т. е. |
|||
|
x→x0 |
|
и x0 |
|
в данном случае x0 X+(x0) |
||||
X−(x0) и, следовательно, x0 X). |
||||
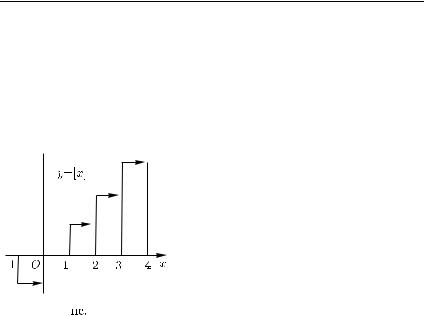
П р и м е р 2. |
Символом [x] |
обозна- |
||
чается целая часть |
числа |
x R, т. е. |
||
наибольшее целое |
число, |
не |
превос- |
|
ходящее x (рис. 62). Таким образом,

 [x] = n Z, n x, но n + 1 > x. Функция y = [x] непрерывна справа во всех точках числовой оси и не является непрерывной слева во всех цело-
[x] = n Z, n x, но n + 1 > x. Функция y = [x] непрерывна справа во всех точках числовой оси и не является непрерывной слева во всех цело-
численных точках x = ±n, n = 0, 1, 2, ...
6.7. Свойства пределов функций. В пп. 6.7–6.12 все рассматриваемые функции определены на некотором фиксированном множестве X R и x0 — его точка прикосновения, конечная или
бесконечно удаленная.
Функция называется ограниченной (сверху или снизу), если мно-
жество ее значений ограничено (соответственно сверху или снизу).
1◦. Если функция f имеет в точке x0 конечный предел, то существует такая окрестность U (x0) точки x0, что функция f ограничена на пересечении X ∩ U (x0).
Если lim f (x) = a R, то существует такая окрестность U (x0)
x→x0
точки x0, что для всех x X ∩ U (x0) выполняется включение f (x)U (a, 1) (здесь в качестве окрестности U (a) в определении 6 взята окрестность U (a, 1)), т. е. неравенство a − 1 < f (x) < a + 1.
С л е д с т в и е. Если функция f непрерывна в точке x0, то существует такая окрестность U (x0) точки x0, что функция f ограни-
чена на
X ∩ U (x0).
Это следует из того, что если функция f непрерывна в точке x0, то она имеет в этой точке конечный предел.

§ 6. Предел и непрерывность функций |
115 |
2◦. Л е м м а 4 (о сохранении знака). Если функция f имеет в точ-
ке x0 не равный нулю конечный предел lim f (x) = a = 0, то суще-
x→x0
ствуют такие окрестность U (x0) точки x0 и число c > 0, что для всех точек x X ∩ U (x0) выполняются неравенства
|
|
|
f (x) > c, |
|
если |
|
|
a > 0; |
|
|
|
|
|
|
|
(6.16) |
||||||||||||||
|
|
|
f (x) < −c, |
|
если |
|
|
|
a < 0. |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Поскольку |
a = 0, |
то |
|
|a| > 0. |
Возьмем в качестве окрестности |
U (a) |
||||||||||||||||||||||||
|
|
2 |
|
|
|
|
||||||||||||||||||||||||
в определении 6 окрестность U |
|
a, |a2| |
|
. Тогда согласно этому опре- |
||||||||||||||||||||||||||
делению существует такая окрестность U (x |
) точки x |
, |
что для всех |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|a| |
|
|
|
точек x X |
|
U (x0) выполняется включение f (x) |
|
U |
a, |
, т. е. |
||||||||||||||||||||||||
справедливо |
неравенство∩ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||
|
|
|
a − |
|a2| |
< f (x) < a + |
|a2| |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||
Отсюда имеем при a > 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
f (x) > a − |
|a2| |
= |
a |
> 0, |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
а при a < 0 |
|
f (x) < a + |
|a| |
= |
|
|
|
+ |
|a| |
= |
|
|
|
|a| |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
a |
− |
< 0. |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
2 |
|
−| | |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||
Таким образом, неравенства (6.16) выполняются при c = |a2|.
С л е д с т в и е. Если функция f непрерывна в точке x0 и f (x0) = 0, то существуют такие окрестность U (x0) точки x0 и постоянная c > 0, что для всех x X ∩ U (x0) выполняются неравенства:
f (x) > c, |
если |
f (x0) > 0; |
f (x) < −c, |
если |
f (x0) < 0. |
Это сразу вытекает из свойства |
2◦, поскольку непрерывность |
|
в точке x0 означает существование у функции f в точке x0 конечного
предела, равного f (x0). В качестве числа c можно взять |f (x0)|.
2
З а м е ч а н и е. Если у функции f в точке x0 существует один из бесконечных пределов ∞, +∞ и −∞, то для л ю б о г о числа c > 0
существует такая окрестность U (x0) точки x0, что для любой точки |
|||||||||
x X ∩ U (x0) выполняются неравенства: |
|
|
|
||||||
f (x) |
| |
> c, |
если |
lim f (x) = |
∞ |
; |
|
||
| |
|
|
|
x x0 |
|
|
|||
|
|
|
|
|
|
→ |
|
|
|
f (x) |
|
> c |
, |
|
если |
lim f (x) = + ; |
|||
|
|
|
x x0 |
∞ |
|
||||
|
|
|
|
|
|
→ |
|
|
|
f (x) < −c |
, |
если |
lim f (x) = |
−∞ |
. |
||||
|
x x0 |
|
|||||||
|
|
|
|
|
|
→ |
|
|
|

116 Гл. 1. Дифференциальное исчисление функций одной переменной
Это следует из определения 5 предела функции, в котором в качестве окрестности U (a) бесконечно удаленной точки в этом случае
следует взять окрестность U a, 1c .
3◦. Если существуют конечные или определенного знака бесконечные пределы lim f (x) = a, lim g(x) = b и a < b, то найдется такая
x→x0 x→x0
окрестность U (x0) точки x0, что для всех точек x X ∩ U (x0) выполняется неравенство
f (x) < g(x).
С л е д с т в и е. Если f (x) g(x), x X, и существуют конечные или определенного знака бесконечные пределы lim f (x), lim g(x), то
|
x→x0 |
x→x0 |
lim f (x) lim g(x). |
|
|
x→x0 |
x→x0 |
|
Выберем непересекающиеся окрестности U (a) и U (b) соответственно точек a и b. Ясно, что если y1 U (a), y2 U (b), то из неравенства a < b следует неравенство
y1 < y2.
Согласно определению предела функции существует такая окрестность U (x0) точки x0, что для всех точек x X ∩ U (x0) выполняются включения f (x) U (a), g(x) U (b) и, следовательно, в силу сказанного выше имеет место неравенство
f (x) < g(x).
В предположениях следствия неравенство
lim f (x) > lim g(x)
x→x0 x→x0
не может выполняться, так как если бы оно имело место, то согласно свойству 3◦ в некоторой окрестности точки x0 имело бы место неравенство f (x) > g(x), что противоречит сделанному в формулировке следствия предположению. Поэтому
lim f (x) lim g(x).
x→x0 x→x0
4◦. Если ϕ(x) f (x) ψ(x), x X и существуют конечные или определенного знака бесконечные пределы lim ϕ(x), lim ψ(x) и они
|
|
|
x→x0 |
x→x0 |
|
равны между собой, то существует lim f (x) |
и |
||||
|
x→x0 |
|
|
||
lim f (x) = lim ϕ(x) = lim ψ(x). |
|||||
x→x0 |
x→x0 |
|
x→x0 |
|
|
5◦. Если f (x) = c — постоянная, x |
|
X, |
то |
||
|
|
|
|||
lim f (x) = c.
x→x0
