
Краткий курс математического анализа. Том 1
.pdf§ 5. Предел числовой последовательности |
97 |
Получающиеся в результате описанной конструкции бесконечные десятичные дроби (5.82) не могут иметь периода, состоящего только из цифры 9. В самом деле, пусть некоторому действительному числу соответствует дробь
α0, α1α2...αn0 99... 9..., n0 0, |
(5.83) |
имеющая период, состоящий из цифры 9 и начинающийся с (n0 + 1)-го места после запятой. Обозначим через {In} последовательность отрезков, соответствующих дроби (5.83) в том смысле, что левым концом отрезка In, n = 1, 2, ..., этой последовательности является число α0, α1α2...αn, получающееся из дроби (5.83) отбрасыванием всех десятичных знаков после запятой, начиная с (n + 1)-го, а правым — число α0, α1α2...αn + 10−n. Такая последовательность отрезков является вложенной системой отрезков, длины которых стремятся к нулю, и, следовательно, существует единственное число a, принадлежащее всем отрезкам In этой системы. Поскольку в дроби (5.83), начиная
с(n0 + 1)-го места после запятой, стоит цифра 9, то точка a, начиная
сотрезков ранга n0 + 1, будет находиться на отрезке с индексом 9, т. е. на самом правом отрезке. Этим свойством обладает только правый конец отрезка In0 , таким образом, число a совпадает с правым концом
отрезка In0 .
При описанной же конструкции соответствия чисел a 0 и бесконечных десятичных дробей (см. (5.72)–(5.82)) всегда предполагалось, что число a не является правым концом ни одного из отрезков соответствующей ему системы вложенных отрезков {In} (см. (5.79)) — в этом состояло одно из условий (5.80). Полученное противоречие показывает, что при указанной конструкции соответствия чисел a 0 и бесконечных десятичных дробей не участвуют дроби вида (5.83), т. е. с периодом, состоящим из одной лишь цифры 9.
Вместе с тем каждая бесконечная десятичная дробь
α0, α1α2...αn..., |
(5.84) |
не имеющая периода, состоящего только из одной цифры 9, оказывается поставленной в соответствие единственному числу a 0, являющемуся точкой пересечения отрезков
In = [α0, α1...αn; α0, α1...αn + 10−n], n = 1, 2, ... |
(5.85) |
В самом деле, последовательность отрезков (5.85) является вложенной системой отрезков, длины которых 10−n стремятся к нулю,
а потому существует единственное число a, принадлежащее всем отрезкам a In, n = 1, 2, ...
Покажем, что дробь (5.84) поставлена в соответствие этому числу a, т. е. что выполнены условия (5.79)–(5.81). Очевидно, следует лишь показать, что число a не является правым концом ни одного из отрезков In. Если бы оказалось, что число a является правым концом
4 Л. Д. Кудрявцев

98 Гл. 1. Дифференциальное исчисление функций одной переменной
некоторого отрезка In0 ранга n0 системы {In}, то число a было бы и правым концом всех отрезков In ранга n > n0, т. е. принадлежало бы отрезкам ранга n > n0 с индексом 9. Это означает, что в дроби (5.84), начиная с (n0 + 1)-го места после запятой, все время стоит цифра 9 — противоречие. Итак, действительно, каждая бесконечная десятичная дробь, не имеющая периода, состоящего из одной цифры 9, поставлена
всоответствие некоторому числу a 0.
Врезультате установлено взаимно однозначное соответствие между всеми неотрицательными действительными числами и всеми бесконечными десятичными дробями, не имеющими периода, состоящего только из цифры 9.
Бесконечные десятичные дроби с периодом, состоящим только из
нуля, обычно записываются в виде конечной десятичной дроби, т. е. вместо α0, α1α2...αn00...0... пишут α0, α1α2...αn.
Подчеркнем, что при конструкции соответствия (5.79)–(5.82) между неотрицательными действительными числами и десятичными дробями это соответствие оказалось взаимно однозначным в силу того, что рассматривались лишь десятичные дроби, не имеющие периода, состоящего только из цифры 9, и требовалось, чтобы никакое a не являлось правым концом ни одного отрезка In соответствующей этому числу a системы {In}. При отказе от выполнения этих условий для каждого числа, являющегося концом некоторого отрезка ранга n, существовали бы две его записи в виде бесконечной десятичной дроби:
α0, α1...αn99...9... = α0, α1...(αn + 1)00...0..., αn = 9,
например,
1 = 1, 00...0 = 0, 99...9...
Ясно, что каждой недопустимой десятичной дроби (т. е. имеющей период из одних девяток) соответствует единственная допустимая десятичная дробь, у которой последняя цифра перед началом периода из девяток увеличена на единицу, а после нее начинается период из одних нулей. Эти две дроби по определению считаются равными.
Если a > 0 и a соответствует дробь α0, α1α2...αn..., то отрицательному числу −a поставим в соответствие ту же дробь, только со знаком минус, и будем писать
−a = −α0, α1α2...αn... |
(5.86) |
Запись действительных чисел в виде (5.82) и (5.86) называется их
десятичной записью.
Бесконечные десятичные дроби ±α0, α1α2...αn..., не имеющие периода, состоящего только из одних девяток, называются допустимыми.
Из всего сказанного видно, что десятичная запись действительных чисел устанавливает между всеми действительными числами и всеми
§ 5. Предел числовой последовательности |
99 |
допустимыми десятичными дробями взаимно однозначное соответствие.
Конечно, нужно не только уметь записывать каждое действительное число в виде десятичной дроби, но и уметь производить с помощью этой записи различные операции над числами: сравнивать их по величине, складывать, вычитать, умножать, делить и т.д. Перейдем к рассмотрению этих вопросов.
Пусть снова a 0 и a = α0, α1α2...αn... Введем обозначения
an = α0, α1...αn, |
|
n = an + 10−n, n = 0, 1, 2, ... |
(5.87) |
||
a |
|||||
Если же a < 0 и a = −α0, α1α2...αn..., то положим |
|
||||
an = −α0, α1α2...αn − 10−n, |
|
n = an + 10−n, n = 0, 1, 2, ... |
(5.88) |
||
a |
|||||
Из этих формул сразу следует, что если b < 0 и b = −a, a > 0, то (рис. 56)
bn = −an, bn = −an, n = 0, 1, 2, ...
(5.89)
Конечная десятичная дробь an (как в случае (5.87), так и в слу-
чае (5.88)) называется нижним десятичным приближением порядка n числа a, а дробь an — его верхним десятичным приближением
того же порядка. Очевидно, что в случае a 0 конечные десятичные дроби an и an являются концами отрезка In (см. (5.80)) последовательности вложенных отрезков {In}, поставленной в соответствие числу a = α0, α1α2...αn..., т. е.
In = [an, |
|
|
n], |
n = 1, 2, ..., |
(5.90) |
|
a |
||||||
и, таким образом, |
|
|
||||
an a |
|
n, |
n = 1, 2, ... |
(5.91) |
||
a |
||||||
В силу соотношений (5.89) система отрезков (5.90) является системой вложенных отрезков и при a < 0; выполняется в этом случае и неравенство (5.91). Из того, что система отрезков (5.90) является системой вложенных отрезков, следует, что
an an+1, |
|
n+1 |
|
n, n = 1, 2, ..., |
(5.92) |
a |
a |
т. е. что последовательность нижних десятичных приближений представляет собой возрастающую последовательность, а верхних — убывающую.
Наконец, из (5.87) и (5.88) непосредственно следует, что
|
|
n − an = 10−n, |
(5.93) |
a |
4*

100 Гл. 1. Дифференциальное исчисление функций одной переменной
а так как lim 10−n = 0, то для любого действительного числа a после-
n→∞
довательность отрезков (5.90) образует систему вложенных отрезков, длины которых стремятся к нулю и единственной точкой пересечения которых является точка a. Отсюда имеем (см. замечание в п. 1.5.7)
lim an = |
lim |
|
n = a. |
(5.94) |
a |
||||
n→∞ |
n→∞ |
|
||
Таким образом, доказано следующее свойство десятичных прибли-
жений.
1◦. Каково бы ни было действительное число a, последовательность его нижних десятичных приближений {an} возрастает, верхних {an} убывает, и имеет место равенство (5.94).
С л е д с т в и е. Всякое действительное число является пределом последовательности рациональных чисел.
В самом деле, нижние и верхние десятичные приближения любого числа, представляя собой конечные десятичные дроби, являются рациональными числами, поэтому утверждение следствия непосредственно вытекает из равенства (5.94).
Перейдем теперь к сравнению по величине действительных чисел
посредством их десятичной записи.
2◦. Если a R, b R, то a < b в том и только том случае, когда существует такое неотрицательное целое число n0, что для всех n > n0 выполняется неравенство
an < bn. |
(5.95) |
Если a < b, то из условия (5.94) согласно свойству 3◦ пределов (п. 1.5.3) сразу следует существование такого n0, что для n > n0 выполняется условие (5.95). Обратно, если существует такое n0, что для всех n > n0 выполняется неравенство (5.95), то, перейдя в нем к пределу при n → ∞, получим a b, но случай a = b невозможен, так как тогда в силу однозначности десятичной записи чисел для всех n = 0, 1, 2, ... имело бы место равенство an = bn, что противоречило бы условию (5.95).
Следовательно, a < b.
С помощью арифметических операций над нижними и верхними десятичными приближениями чисел можно получить нужный результат соответствующих операций над самими числами с любой наперед
заданной точностью. Это видно из следующего утверждения.
3◦. Если a R, b R, то
nlim (an + bn) = a + b, |
nlim (an − bn) = a − b, |
nlim anbn = ab, |
||||
→∞ |
→∞ |
→∞ |
||||
а при b = 0 |
lim |
an |
= |
a |
. |
|
|
|
|
||||
|
n→∞ bn b |
|
||||
§ 5. Предел числовой последовательности |
101 |
Эти формулы сразу следуют из равенств (5.94) и свойств пределов числовых последовательностей (п. 1.5.6). Отметим лишь, что из
условия nlim bn = b = 0 следует существование такого номера n0, что |
|||||
→∞ |
|
|
|||
для всех n > n0 выполняется неравенство bn = 0 (см. следствиеa |
1 |
||||
свойства 3◦ пределов, п. 1.5.3) и при рассмотрении предела lim |
|
n |
|
||
|
|
|
|||
|
|
n→∞ bn |
|||
|
an |
|
|
||
берутся только дроби |
|
, для которых bn = 0, что заведомо имеет |
|||
bn |
|||||
место при n > n0. |
|
|
|||
5.11. Предел последовательности комплексных чисел.
Многие из понятий, введенных для последовательностей действительных чисел, обобщаются на последовательности комплексных
чисел, причем с сохранением ряда свойств.
Комплексное число z0 называется пределом последовательности комплексных чисел {zn}, если для любого ε > 0 существует такой
номер nε, что для всех n > nε выполняется неравенство
|zn − z0| < ε.
В этом случае пишут lim zn = z0 и говорят,
n→∞
что последовательность {zn} сходится к числу z0. Таким образом, по форме это определение
совершенно такое же, как для предела последовательности действительных чисел, однако геометрический смысл его иной: на комплексной плоскости неравенство |z − z0| < ε задает откры-
тый круг (т. е. круг без ограничивающей его окружности) радиуса ε
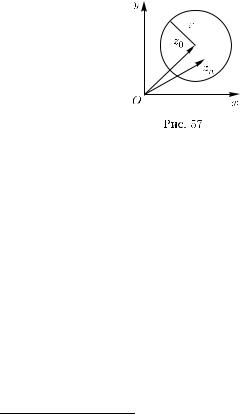
с центром в точке z0. Этот круг называется ε-окрестностью (или, короче, окрестностью) точки z0; будем его обозначать U = U (z0, ε).
Условие lim zn = z0 означает, что, какова бы ни была окрест-
n→∞
ность U точки z0, найдется такой номер n0, что все члены последовательности {zn} с номерами, большими n0, будут содержаться в этой окрестности (рис. 57). Тем самым вне этой окрестности будет находиться только конечное множество членов рассматриваемой последовательности.
Существование предела lim zn = z0 в силу самого определения |
|
n→∞ |
|
предела равносильно существованию предела |
|
nlim |zn − z0| = 0, |
(5.96) |
→∞ |
|
т. е. сходимости к нулю последовательности действительных чисел
|zn − z0|, n = 1, 2, ... |
|
Если zn = xn + yni, z0 = x0 + y0i, xn, yn, x0, y0 R, то |
|
|zn − z0| = (xn − x0)2 + (yn − y0)2 |
(5.97) |

102 Гл. 1. Дифференциальное исчисление функций одной переменной
и, следовательно, |
|
|xn − x0| |z − z0|, |yn − y0| |z − z0|. |
(5.98) |
Из соотношений (5.97), (5.98) следует, что условие nlim |zn − z0| = |
||
= 0 равносильно условиям lim xn = x0, |
lim |
→∞ |
yn = y0. Это означает, |
||
n→∞ |
n→∞ |
= xn + yni, n = 1, 2, ..., |
что последовательность комплексных чисел zn |
||
имеет своим пределом число z0 = x0 + y0i в том и только том случае, когда последовательности действительных {xn} и мнимых {yn} частей членов последовательности {zn} имеют своими пределами со-
ответственно x0 и y0.
Последовательность {zn} комплексных чисел называется ограниченной, если ограничена последовательность действительных чисел {|zn|} (т. е. если ограничена последовательность абсолютных величин членов данной последовательности).
На последовательности комплексных чисел обобщаются многие предложения, доказанные для последовательностей действительных чисел. Так, если последовательность комплексных чисел имеет предел, то он единствен; всякая последовательность комплексных чисел, имеющая предел, ограничена; из всякой ограниченной последовательности комплексных чисел можно выделить сходящуюся; для последовательностей комплексных чисел имеет место аналог критерия Коши сходимости последовательностей действительных чисел; переносятся на последовательности комплексных чисел и свойства пределов, связанные с арифметическими операциями над последовательностями. Все это следует, например, из того, что сходимость последовательности комплексных чисел равносильна сходимости последовательностей их действительных и мнимых частей.
Аналогично случаю последовательностей действительных чисел для последовательностей комплексных чисел определяется и бесконечный предел (без знака, так как комплексные числа не имеют зна-
ка): nlim zn = ∞ означает по определению, что nlim |zn| = +∞. |
|
→∞ |
→∞ |
З а м е ч а н и е. Обычно, когда говорят, что некоторая последовательность комплексных (в частности, действительных) чисел имеет предел, то под этим подразумевают, что этот предел конечный, а случай бесконечного предела оговаривается особо.
§6. Предел и непрерывность функций
6.1.Первое определение предела функции. В дальнейшем
под термином «элемент», «точка» будет пониматься либо действительное число, либо одна из бесконечностей ∞, +∞ и −∞ (бесконечно удаленные точки).

§ 6. Предел и непрерывность функций |
103 |
Сформулируем сначала определение предела функции f : X → R, X R, в терминах пределов последовательностей. Это определение часто называют определением предела функции по Гейне 1).
О п р е д е л е н и е 1. Точка a называется пределом значений функции f (x), x X (или, короче, пределом функции f ), в точке x0 (или,
что то же самое, при x → x0 2), если для любой последовательности точек xn X, n = 1, 2, ..., имеющей своим пределом точку x0, т. е. такой, что
lim xn = x0, |
(6.1) |
n→∞ |
|
последовательность {f (xn)} значений функции f в точках xn, n = = 1, 2, ..., имеет своим пределом точку a, т. е.
|
|
lim |
f (xn) = a. |
|
|
|
|
|
(6.2) |
||
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
В этом случае пишут |
|
|
|
|
|
|
|
|
|
|
|
lim |
f (x) = a |
или |
f (x) |
→ |
a |
при |
x |
→ |
x |
, |
(6.3) |
x x0 |
|
|
|
|
0 |
|
|
||||
→ |
|
|
|
|
|
|
|
|
|
|
|
а если x0 — конечная точка: x0 R, то также
lim f (x) = a.
x−x0→0
В символической записи с помощью логических символов это определение выглядит следующим образом:
lim |
(x) = a |
def |
|
|
|
|
|
||
x x0 f |
|
|
||
→ |
|
|
|
|
def |
|
|
|
nlim f (xn) = a}. (6.4) |
{xn X, n = 1, 2, ...: nlim xn = x0 |
||||
|
|
|
→∞ |
→∞ |
Двоеточием |
здесь, как и раньше в символических формулах |
|||
(см. |
п. 1.1), |
отделяются описания рассматриваемых в условии |
||
элементов. В |
данном |
случае рассматриваются элементы xn X, |
||
n = 1, 2, ..., такие, что |
lim xn = x0. |
|
||
|
|
|
n→∞ |
|
Если в формуле (6.4) a является числом, то говорят, что функция f |
||||
имеет в точке x0 конечный предел (равный a).
Сформулированное определение предела при заданной функции f (x), x X, содержательно только тогда, когда для точки x0 существуют последовательности точек xn X, n = 1, 2, ..., имеющие своим
пределом (конечным или бесконечным) точку x0 : lim xn = x0.
n→∞
1) Г. Гейне (1821–1881) — немецкий математик. 2) Читается «при x, стремящемся к x0».

104Гл. 1. Дифференциальное исчисление функций одной переменной
Оп р е д е л е н и е 2. Пусть X R. Точка x0, для которой существует последовательность xn X, n = 1, 2, ..., имеющая своим пределом
точку x0 |
, |
lim xn = x0 |
, |
(6.5) |
|
|
n→∞ |
|
|
называется точкой прикосновения множества X.
Если точка прикосновения x0 является одной из бесконечностей ∞, +∞ или −∞, то она называется также бесконечно удаленной точкой прикосновения (множества X). Очевидно, что точка
x0 = ∞ является бесконечно удаленной точкой прикосновения множества X тогда и только тогда, когда множество X неограниченно, точка x0 = +∞ — тогда и только тогда, когда множество X неограниченно сверху, а x0 = −∞ — тогда и только тогда, когда X неограниченно снизу.
Очевидно, что любая точка x0, принадлежащая самому множеству X, является его точкой прикосновения, так как стационарная последовательность xn = x0 X, n = 1, 2, ..., удовлетворяет условию (6.5). Точками самого множества не исчерпываются, вообще говоря, все его точки прикосновения: могут существовать точки прикосновения, и не принадлежащие ему. Например, точки x = a и x = b являются точками прикосновения интервала (a, b) и не содержатся в нем.
З а м е ч а н и е 1. Точка является точкой прикосновения данного множества тогда и только тогда, когда любая ее окрестность пересекается с этим множеством.
В самом деле, если x0 — точка прикосновения множества X, то существует последовательность xn → x0, xn X, n = 1, 2, ..., и, следовательно, в любой окрестности точки x0 будут содержаться все члены этой последовательности, начиная с некоторого, и они являются точками множества X.
Наоборот, если в любой окрестности точки x0 имеются точки множества X, то выберем по точке множества X в каждой окрестности U (x0, 1/n) и обозначим эти точки через xn, т. е.
xn X ∩ U (x0, 1/n), n = 1, 2, ...
Если x0 R, т. е. x0 является числом, то xn U (x0, 1/n) означает,
что |xn − x0| < 1/n. Отсюда при n → ∞ следует, что lim |xn − x0| = 0,
n→∞
т. е. lim xn = x0. Если же x0 — бесконечно удаленная точка, напри-
n→∞ 1
мер, x0 = ∞, то xn U (∞, 1/n) означает, что (см. п. 2.2) |xn| > 1/n =
= n. Отсюда при n → ∞ вытекает, что lim xn = ∞. Аналогично
n→∞
рассматриваются случаи x0 = +∞ и x0 = −∞. Таким образом, всегда
из условия xn U (x0, 1/n) следует, что lim xn = x0.
n→∞
Отметим, что нижняя и верхняя грани множества (конечные или бесконечные) являются его точками прикосновения.
§ 6. Предел и непрерывность функций |
105 |
Действительно, если β = sup X, −∞ < β +∞, |
U (β) — какая- |
либо окрестность точки β, и β — левый конец этой окрестности, следовательно, β < β, то согласно определению верхней грани множества существует такая точка x X, что β < x β. Ясно, что x U (β). Это и означает, что верхняя грань β множества X является его точкой прикосновения. Аналогично доказывается, что и нижняя грань множества является его точкой прикосновения.
Поскольку понятие предела функции f : X → R в точке x0 содержательно только тогда, когда эта точка является точкой прикосновения множества X, то в дальнейшем при рассмотрении предела функции f в точке x0 будем всегда предполагать (как правило, специально это не оговаривая), что точка x0 является точкой прикосновения множества X.
П р и м е р ы. 1. Рассмотрим функцию |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
f (x) = |
2x2 + x − 1 |
, |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − 1 |
|
|
|
|
|
|||
определенную на множестве X = R \ {1}. Выясним, существует ли |
|||||||||||||||||||||||
lim |
|
|
|
|
, |
n = |
1, 2, |
... |
, |
и nlim xn = |
0 |
|
|
|
|||||||||
x 0 f (x). Пусть xn X |
|
|
|
|
|
; тогда (п. 5.6) |
|||||||||||||||||
→ |
|
|
|
|
|
xn |
|
|
|
|
|
|
|
|
|
→∞ |
|
xn |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||
|
|
|
|
2xn2 |
+ xn |
− |
1 |
|
|
2 |
|
nlim xn |
+ nlim xn − 1 |
|
|||||||||
lim |
f (xn) = lim |
|
|
|
|
|
|
|
|
= |
|
→∞ |
|
|
→∞ |
= 1. |
|||||||
n |
→∞ |
n |
→∞ |
|
|
|
|
− |
1 |
|
|
|
|
|
|
lim |
|
− |
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
|
|
||||||
Таким образом, существует предел lim f (xn) = 1, а так как он не
n→∞
зависит от выбора последовательности xn → 0, xn X, n = 1, 2, ..., то существует и
lim f (x) = 1.
x→0
2. Рассмотрим функцию
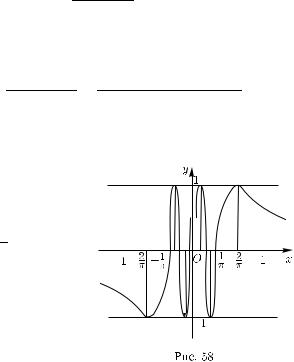
f (x) = sin x1 .
Она определена на множестве X = R \ {0} (рис. 58). Выясним, существует ли предел lim f (x).
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
Возьмем две последовательности: |
|
|
|
|
|
|
||||||||
xn = |
1 |
и xn = |
|
|
1 |
|
, n = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
πn |
π/2 + 2πn |
|
|
|
|
|
|
|
|||||
= 1, 2, ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Очевидно, |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
lim x |
|
= |
lim x = 0, |
x |
n |
X, |
x |
X, |
||||
|
|
n→∞ |
|
n |
|
n→∞ |
n |
|
|
|
n |
|
||
f (xn) = sin πn = 0, |
f (xn |
) = sin |
π |
+ 2πn |
= 1, |
n = 1, 2, ... |
||||||||
2 |
||||||||||||||

106 Гл. 1. Дифференциальное исчисление функций одной переменной
Поэтому |
|
lim f (xn) = 0, |
lim f (xn) = 1, |
n→∞ |
n→∞ |
а это означает, что у рассматриваемой функции не существует предела в точке x0 = 0.
О п р е д е л е н и е 3. Если задана функция f (x), x X, E X и x0 — точка прикосновения множества E, то пределом функции f (x) по множеству E в точке x0 называется предел ее сужения fE
(см. п. 1.2) в этой точке:
lim |
def |
lim fE (x). |
(6.6) |
f (x) = |
|||
x→x0 |
|
x→x0 |
|
x E |
|
|
|
Очевидно, что если существует |
lim f (x), то для любого множест- |
||
x→x0
ва E X, для которого точка x0 является точкой прикосновения,
существует lim f (x), причем эти пределы равны.
x→x0 x E
Иногда при обозначении предела по множеству E вместо x E будут употребляться для краткости другие обозначения, смысл которых
будет ясен из контекста. Например, при E = X \ {x0} будем писать |
|||||||||
x |
lim f (x), |
а при |
E = |
{ |
x |
0 |
|
|
lim f (x). |
x0, x=x0 |
|
|
} будем писать x x0 , x=x0 |
||||||
→ |
|
|
|
|
|
|
|
|
→ |
|
3. Пусть |
|
|
|
|
|
1, |
если |
x Q, |
|
|
|
f (x) = |
||||||
|
|
|
|
|
|
|
0, |
если |
x I. |
|
Эта функция называется функцией Дирихле 1). Имеем |
||||||||
|
|
lim f (x) = 1, |
lim f (x) = 0, |
||||||
|
|
x→0 |
|
|
|
|
x→0 |
|
|
|
|
x Q |
|
|
|
|
x I |
|
|
а предел lim f (x) по всему множеству определения функции f , т. е.
x→0
по всему множеству действительных чисел, не существует.
Часто пределы функций рассматриваются по пересечениям областей определения этих функций с так называемыми проколотыми окрестностями.
О п р е д е л е н и е 4. Проколотой ε-окрестностью |
◦ |
, ε) точ- |
U (x0 |
ки x0 называется множество, получающееся удалением точки x0 из ее
ε-окрестности: |
◦ |
def |
, ε) \ {x0}. |
(6.7) |
|
||||
|
U (x0 |
, ε) = U (x0 |
◦
Проколотую окрестность будем также обозначать и через U (x0).
1) Л. Дирихле (1805–1859) — немецкий математик.
