
Краткий курс математического анализа. Том 1
.pdf
§ 5. Предел числовой последовательности |
87 |
ограничена, ибо для всех n > n0 выполняется неравенство
|
1 |
|
1 |
2 |
|
|
|
|
= |
|
(5<.47) |
|
, |
b(b + βn) |
|b||yn| |
|b|2 |
||||
а последовательность |
{bαn − |
aβn} бесконечно малая как линейная |
||||
комбинация бесконечно малых последовательностей {αn} и {βn}. Поэтому бесконечно малой является и последовательность
1 |
(bαn − aβn) |
b(b + βn) |
как произведение ограниченной последовательности на бесконечно малую.
Следовательно, из равенства (5.48) вытекает, что
lim |
xn |
= |
a |
= |
lim xn |
|
||
n→∞ |
. |
|||||||
|
|
|||||||
n→∞ yn |
|
b lim |
yn |
|
||||
|
|
|
|
|
n→∞ |
|
|
|
5.7. Монотонные последовательности.
О п р е д е л е н и е 8. Верхняя (нижняя) грань множества значе-
ний числовой последовательности {xn} называется верхней (нижней) гранью этой последовательности и обозначается sup {xn} (соответственно inf {xn}).
Иначе говоря, если xn R, n = 1, 2, ..., и если β = sup {xn}, то:
1)для всех n N имеет место неравенство xn β;
2)для любого β < β существует такое n0 N, что xn0 > β .
Аналогично, если α = inf {xn}, то:
1)для всех n N имеет место неравенство xn α;
2)для любого α > α существует такое n0 N, что xn0 < α .
П р и м е р ы.
|
|
1 |
|
|
1 |
|
0, |
|
||
1. |
sup n = 1, |
,inf n = |
n N. |
|||||||
|
1, |
|||||||||
2. |
sup {n} = +∞ |
inf {n} = |
|
n N. |
||||||
О п р е д е л е н и е 9. Числовая последовательность {xn} называется возрастающей (убывающей), если для всех n N выполняется
неравенство xn xn+1 (соответственно неравенство xn xn+1). Возрастающая (убывающая) последовательность обозначается xn ↑ (соответственно xn ↓). Если возрастающая (убывающая) последователь-
ность имеет предел, равный a, то пишут xn ↑ a (соответственно xn ↓ a). Последовательность {xn} называется строго возрастающей (строго убывающей), если для всех n N выполняется неравенство
xn < xn+1 (соответственно неравенство xn > xn+1). Строго возрастающая (строго убывающая) последовательность обозначается xn ↑↑ (соответственно xn ↓↓).
88 Гл. 1. Дифференциальное исчисление функций одной переменной
Убывающие и возрастающие последовательности называются монотонными, а строго убывающие и строго возрастающие — строго монотонными.
П р и м е р ы.
3.Последовательность {1/n} строго убывает.
4.Последовательность {n} строго возрастает.
5.Последовательность {(−1)n} немонотонная.
Те о р е м а 3 (Beйepштpacc 1)). Всякая возрастающая числовая последовательность {xn} имеет предел: конечный, если она огра- ничена сверху, и бесконечный, если она
неограничена сверху, причем |
|
nlim xn = sup {xn}. |
(5.49) |
→∞ |
|
Аналогично, если {xn} — убывающая последовательность, то существует (конечный или бесконеч-
ный) предел |
|
nlim xn = inf {xn}, |
(5.50) |
→∞ |
|
и, следовательно, этот предел конечен, если последовательность {xn}
ограничена снизу, и бесконечен, если она неограничена снизу.
Пусть последовательность {xn} возрастает. Докажем равенство (5.49). Остальные утверждения теоремы для возрастающих последовательностей следуют из него очевидным образом.
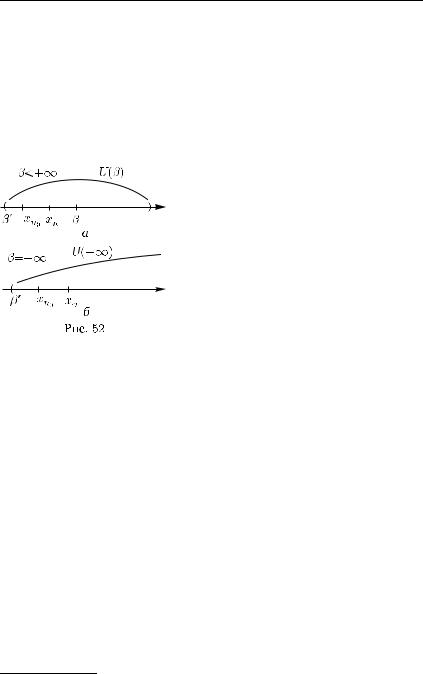
Пусть β = sup {xn}, значение β может быть как конечным, так
ибесконечным. Возьмем произвольную окрестность U (β) точки β
иобозначим через β ее левый конец (рис. 52). Очевидно, β < β. Согласно определению верхней грани:
1)для любого номера n N имеет место неравенство
xn β; |
(5.51) |
2) существует такой номер n0, что |
|
xn0 > β . |
(5.52) |
В силу возрастания последовательности {xn} из (5.51) и (5.52) следует, что для всех номеров n > n0 выполняется неравенство
β < xn0 xn β, |
(5.53) |
и поскольку (β , β] U (β), то при n > n0 имеет место включение
xn U (β), |
(5.54) |
1) К. Вейерштрасс (1815–1897) — немецкий математик.

§ 5. Предел числовой последовательности |
89 |
а это и означает, что β является пределом последовательности {xn}. Аналогично рассматривается случай xn ↓ .
З а м е ч а н и е. Если [an, bn], n = 1, 2, ..., — система вложенных отрезков, длины которых стремятся к нулю, а ξ — точка, принадлежащая всем отрезкам этой системы, то
ξ = lim an = |
lim bn. |
(5.55) |
n→∞ |
n→∞ |
|
В самом деле, последовательность {an} возрастает, а {bn} убывает, кроме того (см. (4.25) в п. 1.4.5), было показано, что ξ = sup {an} = = inf {bn}. Поэтому равенство (5.55) сразу следует из теоремы 3.
П р и м е р 6 (число e). Рассмотрим последовательность
1 n
xn = 1 + n , n = 1, 2, ...,
и покажем, что она строго возрастает и ограничена сверху, а следовательно, согласно теореме 3 имеет конечный предел.
Применив формулу бинома Ньютона, получим
1 |
|
|
n |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
xn = 1 + |
|
|
|
|
|
= |
1 + n |
|
|
+ |
n(n2− |
|
) |
|
|
|
+ ... |
|
|
|
|
|
|
|
|
|
|
|||||||||
n |
|
|
n |
|
n2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
... + |
n(n − 1)(n − 2)...(n − k + 1) |
|
1 |
+ ... + n(n − 1)...1 |
1 |
= |
||||||||||||||||||||||||||||||
|
|
n |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k! |
|
|
|
|
|
|
|
|
|
|
nk |
|
|
|
|
n! |
|
|
n |
|
|
||||
= 1 + 1 + |
1 |
1 |
|
1 |
+ ... + |
1 |
1 |
|
|
|
|
1 |
|
1 |
|
|
2 |
... |
1 |
|
k − 1 |
+ ... |
||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
2 |
|
|
− n |
|
|
|
|
k! |
|
|
− |
|
|
|
−1 |
n |
|
−n |
n |
|
|
||||||||||||
|
|
|
|
|
|
! |
|
|
|
|
|
|
1 |
|
|
|
− |
1 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
+ |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
. (5.57) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− n |
− |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
... |
n |
|
|
||||||||||||||
Из выражения, стоящего в правой части равенства, видно, что при переходе от n к n + 1 число слагаемых (которые все положительны) в написанной сумме возрастает на единицу и каждое слагаемое, начиная с третьего, увеличивается, так как становится больше выражение, стоящее в каждых круглых скобках, ибо
1 − |
s |
< 1 − |
s |
|
, s = 1, 2, ..., n − 1, n = 2, 3, ... |
n |
n + |
1 |
Это означает строгое возрастание последовательности (5.56):
|
|
|
|
|
xn < xn+1, |
n = 1, 2, ... |
(5.58) |
|||||||
Далее, поскольку |
|
|
|
|
|
|
|
|
|
|
|
|
||
1 − |
s |
< 1, |
s = 1, 2, ..., n − 1, n = 2, 3, ..., |
(5.59) |
||||||||||
n |
||||||||||||||
2n−1 = |
1 · 2 · 2 · ... · 2 |
1 · 2 · 3 · ... · n = n!, |
|
|||||||||||
и поэтому |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
n сомножителей |
|
|
|||||||||
|
|
|
1 |
|
1 |
|
, |
|
n = 1, 2, ..., |
(5.60) |
||||
|
|
|
|
|
n! |
2n− |
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||

90 Гл. 1. Дифференциальное исчисление функций одной переменной
то при n > 1 из равенства (5.57) получим |
|
|
|
|
|
|
|
|
|||||||||
xn < 2 + |
1 |
+ |
1 |
+ ... + |
1 |
< 2 + |
1 |
+ 1 |
+ ... + |
1 |
|
|
< |
|
|
||
|
|
n! |
2 |
|
2n−1 |
|
|
|
|||||||||
2! |
3! |
|
|
22 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
∞ |
1 |
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
n = 1 + |
− |
= 3 |
|||||
|
|
|
|
|
|
|
|
|
< 1 + |
|
|
2 |
1 1/2 |
||||
|
|
|
|
|
|
|
|
|
n=0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(мы заменили сумму конечной геометрической прогрессии суммой бесконечной геометрической прогрессии, так как у последней проще формула). Итак,
xn < 3, |
(5.61) |
т. е. последовательность (5.56) ограничена сверху. Из (5.58) и (5.61) следует, что она имеет конечный предел. Он обозначается через e:
|
= |
n→∞ |
+ n |
. |
( . ) |
|
e |
def |
lim 1 |
1 |
|
n |
5 62 |
|
|
|
|
|||
Поскольку 2 < xn < 3 и xn ↑, то 2 < e 3. Можно показать, что e — иррациональное число и что с точностью до 10−15
e≈ 2, 718 281 828 459 045.
5.8.Принцип компактности. Если дана последовательность {xn} и из некоторых ее членов xnk , взятых в порядке возрастания
равносильно nk > nk ), составлена новая после-
довательность {xnk }, то она называется подпоследовательностью последовательности {xn}.
В подпоследовательности {xnk } k является номером члена этой последовательности, а nk — его номером в исходной последователь-
ности. Ясно, что для всех k = 1, 2, ... имеет место неравенство nk k,
и поэтому lim nk = +∞.
k→∞
Подпоследовательности {xnk } последовательности {xn} считаются различными, если они соответствуют различным наборам номеров {nk }. Различные подпоследовательности одной и той же последовательности, рассматриваемые как последовательности, могут оказаться одинаковыми. Так, последовательность xn = 0, n = 1, 2, ..., как и любая последовательность, имеет бесконечно много различных подпоследовательностей (можно, например, выбрать четные номера, нечетные, кратные трем, четырем и т. д.), но все эти подпоследовательности как последовательности совпадают, очевидно, с данной последовательностью xn = 0, n = 1, 2, ...
Выше было показано (см. п. 1.5.4), что если числовая последовательность имеет конечный предел, то она ограничена. Обратное, конечно, неверно. Например, последовательность xn = (−1)n, n = 1, 2, ..., ограничена, но не имеет предела. Вместе с тем, если вся ограниченная последовательность не имеет предела, то у нее всегда
§ 5. Предел числовой последовательности |
91 |
существует подпоследовательность, которая имеет предел. Точнее, имеет место следующий факт.
Те о р е м а 4. Из любой ограниченной числовой последовательности можно выделить сходящуюся подпоследовательность, а из любой неограниченной сверху (неограниченной снизу) числовой последовательности — последовательность, имеющую своим пределом +∞ (соответственно −∞).
Рассмотрим сначала случай, когда последовательность {xn} ограничена, т. е. существуют такие a R и b R, что для всех номеров n выполняется неравенство a xn b.
Разделим отрезок [a, b] на два равных отрезка точкой a + b . Тогда
2
по крайней мере на одном из них — обозначим его [a1, b1] — окажется бесконечно много членов последовательности {xn}. Выберем произвольно какой-либо член этой последовательности, содержащийся в отрезке [a1, b1]. Пусть его номер равен n1:
x |
|
|
[a |
, b ], b |
1 − |
a |
1 |
= |
b − a |
. |
(5.63) |
|
n1 |
1 |
1 |
|
2 |
|
|
||||
Снова разделим отрезок [a1, b1] на два равных отрезка и тот из них, на котором лежит бесконечно много членов последовательности (по крайней мере для одного из них это условие выполняется), обозначим [a2, b2]. Поскольку на отрезке [a2, b2] лежит бесконечно много членов последовательности {xn}, то среди них заведомо есть члены с номерами, большими чем n1. Выберем один из таких членов. Если его номер n2, то
xn2 [a2, b2] [a1, b1], |
n2 > n1, |
(5.64) |
||||||
b |
− |
a |
|
= |
b1 − a1 |
= b − a . |
(5.65) |
|
2 |
|
2 |
2 |
|
22 |
|||
Продолжая этот процесс, получим такую подпоследовательность {xnk } (т. е. n1 < n2 < ... < nk < ...) последовательности {xn}, что
|
|
|
|
ak xnk bk , |
|
|
(5.66) |
||||
|
[ak, bk ] [ak−1, bk−1], |
|
|
(5.67) |
|||||||
b |
− |
a |
|
= |
b − a |
, k = 1, 2, |
... |
, |
(5.68) |
||
k |
|
k |
|
2k |
|
|
|
|
|
||
lim (b |
|
|
a |
) = |
lim |
b − a = 0. |
|
|
|||
и, следовательно, k→∞ |
k − |
k |
|
k→∞ |
2k |
|
|
|
|||
Врезультате получилась система вложенных отрезков [ak , bk ], k =
=1, 2, ..., длины которых стремятся к нулю. Поэтому (см. п. 1.4.5) существует единственная точка ξ, принадлежащая всем этим отрезкам,

92 Гл. 1. Дифференциальное исчисление функций одной переменной
причем (см. (5.55)) lim ak = lim bk = ξ, а тогда в силу свойства 2◦
k→∞ k→∞
пределов (см. п. 1.5.3) из неравенства (5.66) следует, что
lim xnk = ξ.
k→∞
Это означает, что подпоследовательность {xnk } имеет конечный предел, т. е. сходится.
Пусть теперь последовательность {xn}, n = 1, 2, ..., не ограничена сверху. Тогда существует такой номер n1, что xn1 > 1. Поскольку последовательность xn1+1, xn1+2, ..., получающаяся из данной последовательности {xn} отбрасыванием конечного числа ее членов
x1, x2, ..., xn1 , также не ограничена сверху, то найдется такой номер |
|
n2 > n1, что xn2 > 2. Продолжая этот процесс, получим такие чле- |
|
ны xnk последовательности {xn}, что |
(5.69) |
n1 < n2 < ... < nk < ..., |
|
xnk > k, k = 1, 2, ... |
(5.70) |
Условие (5.69) означает, что последовательность {xnk } является подпоследовательностью последовательности {xn}, а из условия (5.70) в силу следствия свойства 2◦ пределов (п. 1.5.3) вытекает, что
klim xnk = +∞. |
(5.71) |
→∞ |
|
Аналогично рассматривается случай последовательности, не ограниченной снизу.
З а м е ч а н и е 1. Первое утверждение теоремы 4, т. е. то, что из
всякой ограниченной числовой последовательности можно выделить сходящуюся, называется теоремой Больцано–Вейерштрасса 1) или принципом компактности отрезка.
З а м е ч а н и е 2. Поскольку всякая неограниченная последовательность не ограничена по крайней мере либо сверху, либо снизу, то из второго утверждения теоремы 4 следует, что всякая неограниченная последовательность содержит бесконечно большую подпоследовательность, причем ее всегда можно выбрать таким образом, что ее пределом будет являться бесконечность со знаком.
О п р е д е л е н и е 10. Предел, конечный или определенного знака бесконечный, подпоследовательности числовой последовательности называется частичным пределом этой последовательности.
Из теоремы 4 следует, что у любой числовой последовательности всегда существует по крайней мере один частичный предел (заведомо конечный, если последовательность ограничена, и бесконечный, если она не ограничена).
1) Б. Больцано (1781–1848) — чешский математик.

§ 5. Предел числовой последовательности |
93 |
5.9. Критерий Коши. В этом пункте дается критерий 1) сходимости последовательности, т. е. критерий существования у нее конечного предела, в терминах только самих членов данной последовательности, иначе говоря, без привлечения значения самого предела.
О п р е д е л е н и е 11. Числовая последовательность {xn}, n = 1, 2, ..., называется фундаментальной последовательностью, если она
удовлетворяет следующему условию: для любого ε > 0 существует такой номер n0, что для всех n > n0 и m > n0 выполняется неравенство
|xn − xm| < ε. |
(5.72) |
Это условие называется условием Коши 2). Его можно записать в несколько другом виде: для любого ε > 0 существует такой номер n0, что для всех n > n0 и всех целых p 0 выполняется неравенство
|xn+p − xn| < ε. |
(5.73) |
Чтобы убедиться в равносильности этих утверждений, достаточно заметить, что из двух номеров m и n всегда один не превышает другого, например, m n, и тогда, положив p = m − n, мы перейдем от записи (5.73) к записи (5.72).
Докажем несколько лемм о фундаментальных последовательностях.
Л е м м а 2. Если последовательность имеет конечный предел, то она фундаментальная.
Действительно, если последовательность {xn} сходящаяся и a —
ее предел: lim xn = a, то согласно определению предела для любого
n→∞
ε > 0 существует такой номер n0, что для всех n > n0 выполняется неравенство
|
|
|
|
|
|
|
|xn − a| < ε/2. |
|
|
|
|
|
(5.74) |
|||||
Поэтому если m > n0 и n > n0, то |
|
|
|
|
|
|
|
|
|
|||||||||
x |
x |
m| |
= (x |
n − |
a) + (a |
− |
x |
) |
x |
a |
+ x |
a |
< |
ε |
+ |
ε |
= ε. |
|
|
|
|||||||||||||||||
| n − |
|
| |
|
|
m |
| | n − |
| |
| m − |
|
| (5.74) 2 |
2 |
|
||||||
Л е м м а 3. Если последовательность фундаментальная, то она ограниченная.
Действительно, пусть последовательность {xn} фундаментальная. Тогда согласно условию Коши существует такой номер n0, что для всех m > n0 и n > n0 имеет место неравенство
|xn − xm| < 1 |
(5.75) |
1) Термин «критерий» употреблен здесь в смысле «необходимое и достаточное условие».
2) О. Кош´и (1789–1857) — французский математик.

94 Гл. 1. Дифференциальное исчисление функций одной переменной
(в условии Коши (см. определение 11) можно взять любое ε > 0; мы
взяли здесь ε = 1). В частности, при m = n0 + 1 из (5.75) следует, что |xn − xn0+1| < 1, или
xn0+1 − 1 < xn < xn0+1 + 1, n = n0 + 1, n0 + 2, ...,
т. е. последовательность xn0+1, xn0+2, ..., получающаяся из данной последовательности {xn} отбрасыванием первых ее n0 членов x1, x2, ...
..., xn0 , является ограниченной последовательностью. Поэтому ограничена, очевидно, и вся последовательность {xn}.
Л е м м а 4. Если некоторая подпоследовательность фундаментальной последовательности сходится, то ее предел является и пределом всей последовательности.
Пусть {xn} — фундаментальная последовательность, {xnk } — ее сходящаяся подпоследовательность и
lim xnk = a. |
(5.76) |
k→∞ |
|
Зададим произвольно ε > 0. Согласно условию Коши существует такой номер n0, что для всех n, m > n0 выполняется неравенство
|xn − xm| < ε/2. |
(5.77) |
В силу определения подпоследовательности имеем lim nk = ∞.
k→∞
Поэтому существует такой номер k0, что nk0 > n0, а так как в подпоследовательности сохраняется тот же порядок членов, что и в самой последовательности, то при k > k0 выполняется и неравенство nk > nk0 . Следовательно, при k > k0 имеет место неравенство
nk > n0. |
(5.78) |
Таким образом при всех n > n0 и k > k0 справедливо неравенство
|xn − xnk | < 2ε .
(5.77) (5.78)
Перейдя здесь к пределу при k → ∞, в силу условия (5.76) получим, что для всех n > n0 выполняется неравенство
|xn − a| 2ε < ε.
Это и означает, что lim xn = a.
k→∞
Те о р е м а 5 (критерий Коши). Для того чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она удовлетворяла условию Коши.
Действительно, необходимость выполнения условия Коши для сходящейся последовательности составляет содержание леммы 2.
§ 5. Предел числовой последовательности |
95 |
Если же последовательность удовлетворяет условию Коши, т. е. является фундаментальной, то согласно лемме 3 она ограничена, и, следовательно, в силу принципа компактности (см. теорему 4) из нее можно выделить подпоследовательность, имеющую конечный предел. Тогда из леммы 4 следует, что вся заданная последовательность сходится к тому же пределу.
У п р а ж н е н и е. Доказать, что не всякая фундаментальная последовательность рациональных чисел имеет рациональный предел.
5.10. Изображение действительных чисел бесконечными десятичными дробями. Пусть задано действительное число a 0.
В силу принципа Архимеда существует натуральное число n > a. В множестве чисел 1, 2, ..., n возьмем наименьшее среди тех, которые больше числа a, т. е. такое натуральное число n0, что
n0 − 1 a < n0.
Обозначим n0 − 1 через α0, а отрезок [α0, α0 + 1] — через I0. Тогда
a I0 = [α0; α0 + 1], a = α0 + 1 |
|
(поскольку в этом пункте концы от- |
|
резков будут обозначаться десятич- |
|
ными дробями, то в качестве раз- |
|
делительного знака между концами |
|
отрезков удобнее употреблять не за- |
|
пятую, а точку с запятой, т. е. вместо |
|
[a, b] писать [a; b]). |
|
Разобьем отрезок I0 на 10 рав- |
|
ных отрезков и каждому отрезку сле- |
|
ва направо припишем последователь- |
|
но индексы 0, 1, 2, ..., 9. Точка a либо |
|
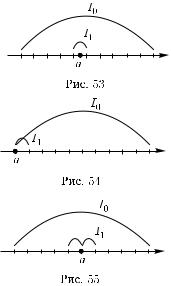
принадлежит только одному из этих |
|
отрезков, |
обозначим его I1 (рис. 53 |
и рис. 54), |
либо двум соседним, ес- |
ли она является их общим концом |
|
(рис. 55). В последнем случае для од- |
|
нозначности выбора отрезков обозна- |
|
чим через I1 тот из двух соседних отрезков, для которого точка a является
левым концом (целесообразность такого выбора будет пояснена ниже). Итак, в обоих случаях точка a лежит на отрезке I1 и не является его правым концом.
Обозначим левый конец отрезка I1 десятичной дробью α0, α1, где |
||||||||||
α1 — индекс отрезка I1 (одна из цифр 0, 1, 2, ..., 9), тогда правый конец |
||||||||||
будет записываться числом α0, α1 + 10−1. Таким образом, |
||||||||||
a |
|
I |
1 |
= [α , α ; α , α + 10−1], |
a = α , α + 10−1. |
|||||
|
|
0 |
1 |
0 |
1 |
|
0 |
1 |
||

96 Гл. 1. Дифференциальное исчисление функций одной переменной
Разобьем отрезок I1, в свою очередь, на десять равных отрезков и обозначим через I2 = [α0, α1α2; α0, α1α2 + 10−2] тот из них, который
содержит точку a, причем она не является его правым концом. Продолжая этот процесс, получим систему вложенных отрезков
I0 I1 I2 ... In ..., |
(5.79) |
содержащих точку a, причем она не является правым концом ни одного из них:
a In = [α0, α1...αn; α0, α1...αn + 10−n], |
(5.80) |
||||
a = α , α1 |
α + 10−n, n = 1, 2, |
... |
|
||
|
0 |
... n |
|
|
|
Поскольку длина отрезка In равна 10−n и |
lim 10−n = 0, то точка a |
||||
n→∞
является единственной точкой, принадлежащей всем отрез кам In, n = 1, 2, ... Отрезок In будем называть отрезком ранга n.
Таким образом, каждому действительному числу a 0 однозначным образом поставлена в соответствие последовательность вложенных отрезков {In}, длины которых стремятся к нулю. А именно,
последовательность {In}, пересечение отрезков которой состоит из |
||
числа a: |
n |
|
|
∞ |
|
|
=1 In = {a}. |
(5.81) |
При этом разным числам оказываются поставленными в соответствие разные последовательности вложенных отрезков {In}, так как в силу стремления к нулю длин отрезков In пересечение рассматриваемой последовательности {In} состоит из единственной точки a и, следовательно, разные точки числовой прямой принадлежат разным последовательностям {In}, т. е. на некотором n-м шаге они окажутся в разных отрезках ранга n.
Каждая последовательность {In}, очевидно, полностью описывается последовательностью своих левых концов α0, α1α2...αn (правый конец получается добавлением числа 10−n к левому концу), n = 1, 2, ..., а следовательно, и бесконечной десятичной дробью α0, α1α2...αn..., так как левый конец каждого отрезка In получается из этой бесконечной десятичной дроби отбрасыванием всех ее цифр после запятой, начиная с (n + 1)-й.
В результате каждому действительному числу a 0 оказывается поставленной в соответствие указанным образом бесконечная десятичная дробь α0, α1α2...αn... Если числу a соответствует дробь
α0, α1α2...αn..., то пишут |
|
a = α0, α1α2...αn... |
(5.82) |
Подчеркнем, что в этой записи через a0 обозначается соответствующее
неотрицательное целое число, а через an, n = 1, 2, ..., — одна из цифр
0, 1, 2, ..., 9.
