
Краткий курс математического анализа. Том 2
.pdf
290 Гл. 6. Гармонический анализ
где δ, 0 < δ π, произвольно фиксировано. При этом если указанные пределы существуют, то они равны.
Таким образом, несмотря на то, что коэффициенты ряда Фурье функции определяются с помощью ее значений на всем отрезке [−π, π] (как говорят, на всем периоде), сходимость ее ряда Фурье в любой точке x [−π, π], а в случае сходимости этого ряда его — сумма, зависят только от поведения функции в сколь угодно малой окрестности рассматриваемой точки x.
Действительно, из |
формулы (51.41) следует, |
что пределы |
|
|
δ |
|
|
nlim Sn(x; f ) и |
nlim |
Dn(t)[f (x + t) + f (x − t)] dt |
одновременно |
→∞ |
→∞ |
|
|
0
существуют или нет, а если существуют, то они равны. Предел же указанного интеграла зависит лишь от значений функции на интервале (x − δ, x + δ).
51.5. Сходимость ряда Фурье в точке. Займемся теперь более детальным изучением поведения сумм Фурье Sn(x; f ) в зависимости от поведения функции в окрестности точки x. Предварительно докажем одну лемму.
Л е м м а 4. Если функция f абсолютно интегрируема на отрезке [0, π], то интегралы
ππ
|
|f (t)| |
dt, |
|f (t)| |
dt |
(51.45) |
|
|
t |
|
0 2 sin |
t |
|
|
0 |
|
|
2 |
|
|
|
одновременно сходятся или расходятся.
Поскольку функция f абсолютно интегрируема на отрезке [0, π], то существует такое η, 0 < η π, что, каково бы ни было ξ, функция f интегрируема по Риману на отрезке [ξ, η] (см. замечание 1 в п. 51.1). Для исследования сходимости интегралов
η |
|
|
|
|
η |
|
|
|
|
|
|f (t)| |
dt, |
|
|
|f (t)| |
dt |
(51.46) |
||
|
t |
|
|
|
|
0 2 sin |
t |
|
|
0 |
|
|
|
|
|
2 |
|
|
|
можно применить признак сравнения (см. п. 29.3). |
|
||||||||
Поскольку |
|
2 sin |
t |
|
|
|
|
||
|
|
|
|
|
|
||||
|
lim |
2 |
= 1, |
|
|
|
|||
|
|
|
|
|
|||||
|
t |
|
|
|
|
||||
|
|
0 |
|
|
|
|
|
|
|
|
t→ |
|
|
|
|
|
|
|
|
то подынтегральные функции в интегралах (51.46) эквивалентны при
t → 0: |
|f (t)| |
|
|f (t)| |
, t |
→ |
0. |
||
|
t |
2 sin |
t |
|
|
|||
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|






296 Гл. 6. Гармонический анализ
Так как |
π |
|
Sn(x) = |
Dn(t)f (x + t) dt |
(51.54) |
−π
(см. лемму 3 в п. 51.4), то из формул (51.52) и (51.53) следует, что
π |
|
σn(x) = Φn(t)f (x + t) dt. |
(51.55) |
−π
Л е м м а 5. Ядра Фейера имеют следующие свойства:
1) они являются непрерывными, четными, 2π-периодическими функциями;
ππ
2) |
Φn(t) dt = 2 Φn(t) dt = 1; |
|
(51.56) |
|||||||||
|
−π |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
+ 1 |
t2 |
t , если |
t = 2πm, |
|
||||
|
sin2 n 2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n + 1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
Φn(t) = |
2π(n + 1) sin |
|
2 |
|
|
|
(51.57) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
, |
|
|
|
|
если |
t = 2πm, |
|
|
|
= 0, |
1, 2, |
|
, |
|
n = 0, 1, 2, |
... |
|
||||
|
m |
± |
|
± ... |
|
|
|
|
|
|||
С л е д с т в и е 1. Ядра Фейера неотрицательны: |
|
|||||||||||
|
|
Φn(t) 0, t R. |
|
|
(51.58) |
|||||||
С л е д с т в и е 2. При любом δ, 0 < δ π, выполняется условие
lim max Φn(t) = 0. |
(51.59) |
n→∞ δ |τ| π |
|
Свойства 1) и 2) вытекают из соответствующих свойств ядер Дирихле. Например,
π |
|
|
n |
π |
|
n |
−π |
|
1 |
|
−π |
1 |
|
|
Φn(t) dt = |
|
|
Dk(t) dt = |
|
1 = 1. |
|
(51.53) n + 1 |
k=0 |
|
n + 1 |
k=0 |
|
|
|
|
|
|
||
Отсюда в силу четности ядер Фейера следует второе равенство (51.56). Докажем свойство 3). Если t = 2πm, m = 0, ±1, ±2, ..., то, вспом-
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n(n + 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нив, что |
k = |
|
, получим |
|
|
|
|
|
|
|
|
|
|
||||||
|
k=0 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
2 |
= |
|
1 |
|
2 |
= |
|
1 |
|
|
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
||||||
Φn( πm) |
(51.53) n |
+ 1 k=0 Dk( πm) (51.37) π(n + 1) k=0 k + |
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
+ 1) |
|
n |
+ 1 |
|
n + 1 |
|
|||
|
|
|
|
|
|
= |
|
|
n(n2 |
+ |
|
= |
|
. |
|||||
|
|
|
|
|
|
|
π(n + 1) |
|
2 |
2π |
|||||||||
|
|
|
|
|
|
§ 51. Тригонометрические ряды Фурье |
|
|
|
|
|
|
|
|
|
|
297 |
||||||||||||||||||||||||||||||
|
Если же t = 2πm, m = 0, ±1, ±2, ..., |
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Φn(t) = |
|
|
1 |
|
|
Dk(t) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
n + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
k=0 |
|
|
(51.37) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
= |
|
|
|
|
|
|
t |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
2 |
t |
2 |
|
|
= |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
sin |
k + |
1 |
|
|
|
t |
|
|
|
|
|
n |
|
2 sin |
t |
sin k + |
1 |
t |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
(51.37) |
n + 1 |
|
k=0 |
2π sin |
|
|
|
|
|
|
|
|
|
|
n + 1 |
k=0 |
|
|
|
|
|
|
|
4π sin |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[cos kt − cos(k + 1)t] = |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
4π(n + 1) sin2 |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin2 |
n + 1 |
t |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1 − cos(n + 1)t |
|
|
|
|
|
. |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
2 |
|
|
|
t |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
t |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4(n + 1)π sin |
|
|
|
|
|
2π(n + 1) sin |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|||||||||||||||||
|
Следствие 1 вытекает из формулы (51.57). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
Докажем следствие 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
При любом δ, 0 < δ π, имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin2 n + 1 t |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||
0 |
|
|
|
max Φ |
|
|
(t) |
|
= |
|
max |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 δ → |
0 |
||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
2 t |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
δ |
t |
π |
|
(51.57) δ |
t |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
(51.58) |
|
|
| | |
|
|
|
|
|
|
|
| | |
|
|
|
2(n |
+ 1)π sin |
|
|
|
|
|
|
|
2(n + 1)π sin |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||
при n → ∞. Отсюда сразу следует условие (51.59).
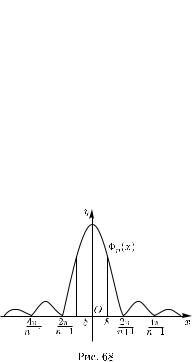
Примерный вид графика ядра Фейера изображен на рис. 68. Образно говоря, ядра Фейера представляют собой такие неотрицательные функции, существенные значения которых при возрастании n
все больше и больше сосредо- |
|
точиваются |
в окрестности ну- |
ля в том смысле, что при лю- |
|
бом δ, 0 < δ π, их значения |
|
вне δ-окрестности нуля равномер- |
|
но стремятся к нулю (см. (51.59)), |
|
а интегралы от этих функций все |
|
время сохраняют постоянное зна- |
|
чение (см. (51.56)). |
|
Пусть функция f непрерывна |
|
на отрезке [−π, π] и принимает |
|
на концах |
одинаковые значения, |
f (−π) = f (π); тогда ее периодическое продолжение с периодом 2π непрерывно на всей действительной оси. В силу непрерывности функции f абсолютная величина ее значений на отрезке [−π, π] ограничена сверху некоторой постоянной c > 0: |f (x)| c, x [−π, π]. Очевидно, что и абсолютные величины всех значений указанного ее периодического продолжения (которое будем обозначать той же буквой f ) ограничены той же постоянной c:
|f (x)| c, x R. |
(51.60) |
