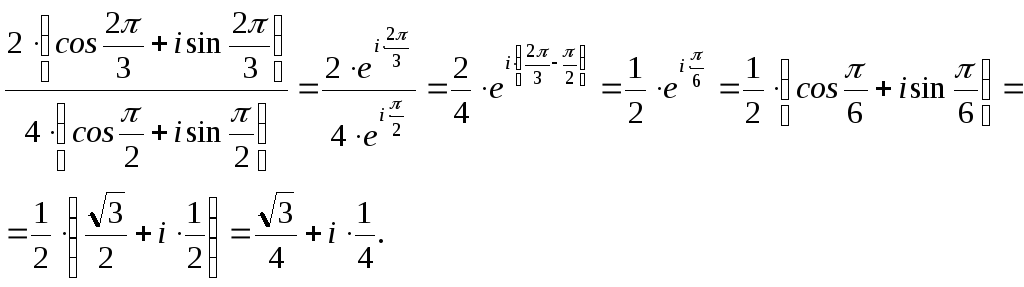- •Раздел 1. Комплексные числа.
- •1.1.1 Основные определения.
- •Арифметические действия над комплексными числами. Сопряженные комплексные числа. Свойства операции сопряжения.
- •1.1.4 Геометрическое изображение комплексных чисел. Комплексная плоскость.
- •1.2 Тригонометрическая форма комплексного числа и
- •1.2.1. Модуль и аргумент комплексного числа.
- •1.2.2 Тригонометрическая и показательная формы комплексного числа.
- •1) ; 2); 3).
- •1.2.3 Умножение и деление комплексных чисел в тригонометрической и показательной форме.
- •Формула Муавра.
- •1.2.4 Деление комплексных чисел в тригонометрической и показательной форме.
- •1.2.5 Извлечение корня любой степени из комплексного числа.
1.2.2 Тригонометрическая и показательная формы комплексного числа.
Пусть
комплексное число
![]() имеет модуль
имеет модуль![]() и главный аргумент
и главный аргумент![]() .
Используя формулы (4), получим
.
Используя формулы (4), получим
![]() .
(5)
.
(5)
Определение 2. Представление комплексного числав виде (5) называется
тригонометрической формой числа .
В случае,
когда -
действительное число, т.е.![]() ,
тригонометрическая форма имеет вид
,
тригонометрическая форма имеет вид![]() при
при![]() и
и![]() при
при![]() ;
при
;
при![]()
![]() может быть каким угодно.
может быть каким угодно.
Для простоты письма введем сокращенное обозначение:
![]() ,
,
тогда тригонометрическая форма (5) примет компактный вид:
![]() .
(6)
.
(6)
Определение 3. Представление комплексного числав виде (6) называется
показательной формой числа ..
Пример.Представить в тригонометрической и показательной форме комплексные числа:
1) ; 2); 3).
Решение.1) Находим модуль данного числа:![]() .
Далее, так как
.
Далее, так как![]() ,
,![]() ,
то
,
то![]() .
Итак,
.
Итак,
![]() .
.
2) Имеем
![]() ,
,![]() (точка, изображающая данное число,
принадлежит положительной части мнимой
оси). Поэтому
(точка, изображающая данное число,
принадлежит положительной части мнимой
оси). Поэтому
![]() .
.
3) Находим
![]() ,
,![]() (данное число является отрицательным
действительным числом). Значит,
(данное число является отрицательным
действительным числом). Значит,
![]() .
.
1.2.3 Умножение и деление комплексных чисел в тригонометрической и показательной форме.
Тригонометрическую и показательную форму комплексного числа удобно использовать при выполнении операции умножения и деления комплексных чисел.
Пусть
 (7)
(7)
-
комплексные числа, заданные в
тригонометрической форме и показательной
формах. Пользуясь элементарными
формулами тригонометрии и определением
умножения, для произведения
![]() в тригонометрической форме получим
соотношение
в тригонометрической форме получим
соотношение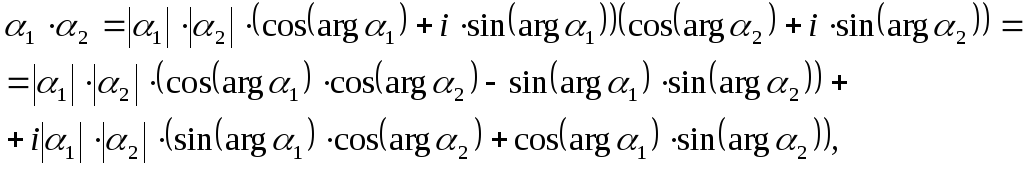
откуда
![]() (8)
(8)
Для показательной формы имеем:
![]() (8*)
(8*)
Из равенства (8) и (8*) следует, что при умножении комплексных чисел модуль произведения равен произведению модулей
![]() ,
(9)
,
(9)
а аргумент произведения равен сумме аргументов сомножителей
![]() . (10)
. (10)
Используя метод математической индукции, можно распространить формулы (8) и (8*) на любое число псомножителей:
![]() (11)
(11)
или
![]() (11*)
(11*)
Пример.Выполнить умножение![]() .
.
Решение.
Сначала найдем модуль и аргумент числа![]() .
Имеем
.
Имеем![]() ,
,![]() .
Запишем
.
Запишем![]() в тригонометрической и показательной
форме:
в тригонометрической и показательной
форме:
![]() ;
;![]() .
.
Теперь
воспользуемся формулой (8)

или
![]() .
.
Формула Муавра.
Полагая в формулах (11) и (11*)
![]() ,
получим
,
получим
![]() (12)
(12)
и
![]() (12*)
(12*)
Формулы (12) и (12*) называются формулами Муавра.
Пример.Найти![]() .
.
Решение.Представим число![]() в
тригонометрической форме и применим
формулу Муавра:
в
тригонометрической форме и применим
формулу Муавра:

Для показательной формы имеем:
 .
.
Следовательно,
![]() .
.
1.2.4 Деление комплексных чисел в тригонометрической и показательной форме.
Для
тригонометрической формы комплексных
чисел 1
и 2, где![]() ,
рассмотрим число
,
рассмотрим число
![]() .
.
Согласно правилу умножения комплексных чисел в тригонометрической форме, имеем

т.е.
![]() или
или![]() .
Итак, для тригонометрической формы
комплексных чисел имеем:
.
Итак, для тригонометрической формы
комплексных чисел имеем:
![]() .
(13)
.
(13)
Для показательной формы имеем

и
![]() (13*)
(13*)
Из
равенств (13) и (13*) получаем, что при
делении комплексных чисел
![]() модуль частного равен отношению
модулей
модуль частного равен отношению
модулей
![]() ,
(14)
,
(14)
а аргумент частного равен разности аргументов числителя и знаменателя
![]() .
(15)
.
(15)
Пример.Выполнить деление .
.
Решение.Так как числа записаны в тригонометрической форме, то по формуле (13) имеем:

Запишем решение в показательной форме: