
7.2.3 Аппроксимация Чебышева
При аппроксимации частотной характеристики ФНЧ полиномами Чебышева при одинаковом числе звеньев n обеспечивается большее затухание в полосе заграждения по сравнению приближением АЧХ по Баттерворту. При такой аппроксимации нормированная частотная характеристикаY(S) задается формулой:
![]()
(7.9)
где ζ<1- постоянное число, называемое коэффициентом неравномерности характеристики в полосе пропускания,
Тn(S)-полином Чебышева порядкаn:
![]() (7.10)
(7.10)
Если перейти в область комплексного переменного, то можно получить выражение полинома Чебышева в бесконечном интервале нормированных частот:
 . (7.10/)
. (7.10/)
Полиномы Чебышева имеют следующие особенности:
![]() в
интервале –1<S<+1
функцияТn(S)
заключена между –1 и+1. Поэтому выбирая
коэффициент неравномерности ζ достаточно
малым, можно аппроксимировать функциюY(S)
сколь угодно близко к единице в полосе
пропускания при любом порядке фильтра.
в
интервале –1<S<+1
функцияТn(S)
заключена между –1 и+1. Поэтому выбирая
коэффициент неравномерности ζ достаточно
малым, можно аппроксимировать функциюY(S)
сколь угодно близко к единице в полосе
пропускания при любом порядке фильтра.
В
![]() приS>>1.В результате
затухание в полосе заграждения с
увеличениемSрезко
увеличивается. Так в приведенном выше
примере приSЗ=3
иn=4 фильтр
Баттерворта обеспечивал затухание
равное 30дБ.
приS>>1.В результате
затухание в полосе заграждения с
увеличениемSрезко
увеличивается. Так в приведенном выше
примере приSЗ=3
иn=4 фильтр
Баттерворта обеспечивал затухание
равное 30дБ.
Фильтр Чебышева при тех же условия и коэффициенте неравномерности в полосе пропускания равном ζ=0,5 вызывает затухание сигнала равное:
![]()
т.е. на порядок выше, при этом максимальное отклонение нормированной АЧХ в полосе пропускания не превышает:
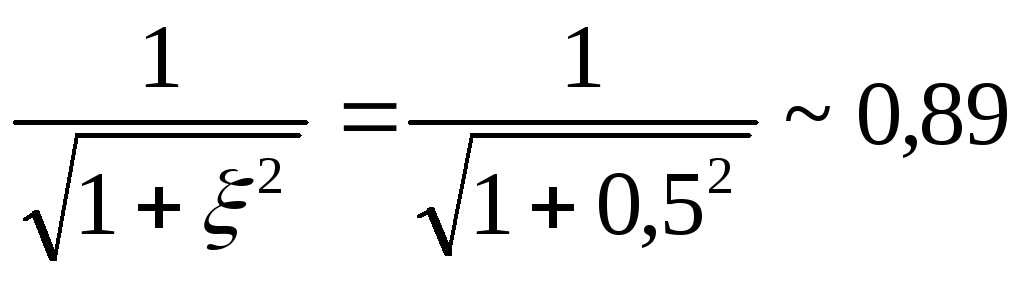 или 20|lg1,11|~0,969дБ.
или 20|lg1,11|~0,969дБ.
Необходимый порядок фильтра Чебышева находится при удовлетворении следующего соотношения:
![]()
где МЗ- необходимая величина затухания фильтра в полосе заграждения в децибелах на нормированной частотеSЗпри заданной неравномерности АЧХ в полосе пропускания -ζ.
В технической литературе посвященной проектированию и расчету активных фильтров помимо формул приводятся номограммы для определения порядка фильтров Чебышева, Баттерворта и других типов на основании технических требований к ним.[4,5]
Полюсы фильтров Чебышева находятся из соотношения аналогичного (7.6) Очевидно, для этого необходимо исследовать уравнение:
![]() . (7.11)
. (7.11)
Метод решения уравнения (7.11) достаточно громоздкий. Окончательный результат состоит в том, что после определения порядка фильтра Чебышева- nЧ(например, с помощью номограмм в[4,5]), находят нормированные полюсы фильтров БаттервортаnБв предположении, что порядок этих фильтров одинаковый:
nЧ=nБ.
Далее вычисляется вспомогательный параметр:

Переход к полюсам фильтра Чебышева осуществляется умножением действительных частей полюсов Баттерворта на Sh(a), а мнимых- наCh(a). Таким образом, полюсы фильтров Чебышева располагаются не на окружности единичного радиуса, как у фильтров Баттерворта, а на эллипсе, уравнение которого в плоскости комплексного переменногоР=σ+jSимеет вид:
 (7.12)
(7.12)
Структура фильтра Чебышева определяется также, как и фильтров Баттерворта, т.е. действительному полюсу соответствуетзвено первого порядка, а двум комплексно-сопряженным полюсам-звено второго порядка.
После определения порядка фильтра
(Баттерворта или Чебышева) и его полюсов
можно записать коэффициент передачи
устройства выраженный через нормированную
S, а затем и ненормированнуюωчастоту с тем, чтобы получить
возможность до реализации звеньев
фильтра проверить соответствие его
частотной характеристики требованию
технического задания. Приn=1
фильтр содержит только одно звено-первого
порядка. Каждому звену второго порядка
соответствует произведение двух
комплексно- сопряженных полюсов или
корней знаменателя нормированного
коэффициента передачиK(P):
(P-Pi)(P-Pi*)
Учитывая, что:![]()
где αiβi-действительные и мнимые части этих полюсов, получим:
![]()
Следовательно, коэффициент передачи К(P) может быть записан:
(7.13)
Коэффициенты 2αj=Вj, (αj2+βj2)=Cjназываются полиномиальными, они однозначно определяются при известномnиз таблицы 7.1 для фильтров Баттерворта или с учетом (7.12)- для фильтров Чебышева. В выражении (7.13) первый нормированный полюс равен –1, поэтому (P-P1)=(P+1).
Для фильтров Баттерворта К(0)=1, поскольку
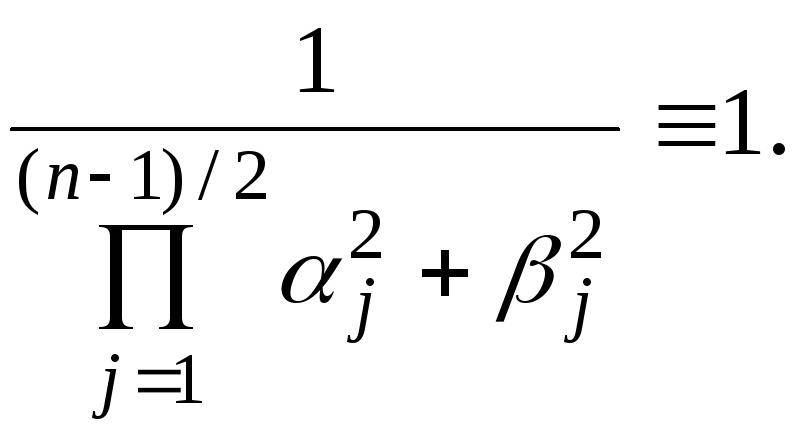 (7.14)
(7.14)
Действительно, нормированные полюсы
такого фильтра с координатами αj,βjв комплексной
плоскости всегда расположены на единичной
окружности, следовательно, квадрат
длины модуля вектора полюсов равен
единице:![]() ,
поэтому справедливо выражение (7.14) т.е.
коэффициентыСjдля таких фильтров всегда равны единице.
В фильтрах Чебышева нормированные
полюсы расположены на эллипсе и условие
(7.14) не выполняется.
,
поэтому справедливо выражение (7.14) т.е.
коэффициентыСjдля таких фильтров всегда равны единице.
В фильтрах Чебышева нормированные
полюсы расположены на эллипсе и условие
(7.14) не выполняется.
Переход от коэффициента К(P) к комплексному коэффициенту передачи фильтраК(jω) производится заменой в (7.13) аргументаPнаjω/ωСР, гдеωСР- частота среза, и переходом от нормированных полюсовPiк ненормированным. Частотная характеристика фильтра записывается обычным образом, т.е. как зависимость модуля его комплексного коэффициента передачи |К(jω)| от частоты.
