-
Операции над множествами
Во
многих случаях удается избежать
противоречий наивной теории множеств,
если выбрать некоторое так называемое
универсальное
множество
и ограничиться рассмотрением только
его подмножеств.
Если некоторые множества взять в качестве исходных, то из них можно получить новые с помощью следующих операций.
Объединением
множеств
и
(обозначение
)
называется множество, состоящее из всех
тех элементов, которые принадлежат хотя
бы одному из множеств
или
:
.
Вместо
символа объединения
используется
также символ +.
Пересечением
множеств
и
(обозначение
)
называется множество, состоящее из
элементов, принадлежащих каждому из
множеств
и
:
.
Для операции пересечения используются также другие обозначения:
.
Аналогично
определяются объединение и пересечение
произвольной совокупности множеств
,
.
Здесь
– множество индексов. Если
– множество
первых натуральных чисел, то употребляются
обозначения
и
,
а в случае если
,
то будем писать
и
.
Разностью
множеств
и
(обозначение
)
называется множество, состоящее из всех
элементов
,
не принадлежащих
:
.
В
отличие от двух предыдущих операций
разность некоммутативна:
.
Если
,
то
.
Симметрической
разностью множеств
и
(обозначение
)
называется множество элементов
и
,
которые содержатся только в одном из
этих множеств:
.
Дополнением
к
множеству
(обозначение
)
относительно универсального множества
называется множество:
или
.
Операции объединения, пересечения и дополнения часто называют булевыми операциями над множествами. Так как операция разности не обладает свойством ассоциативности, то ее выражают через другие операции, например, операции дополнения и пересечения:
.
Универсальное множество позволяет геометрически изображать множества и операции над ними с помощью диаграмм Венна (рис. 1).
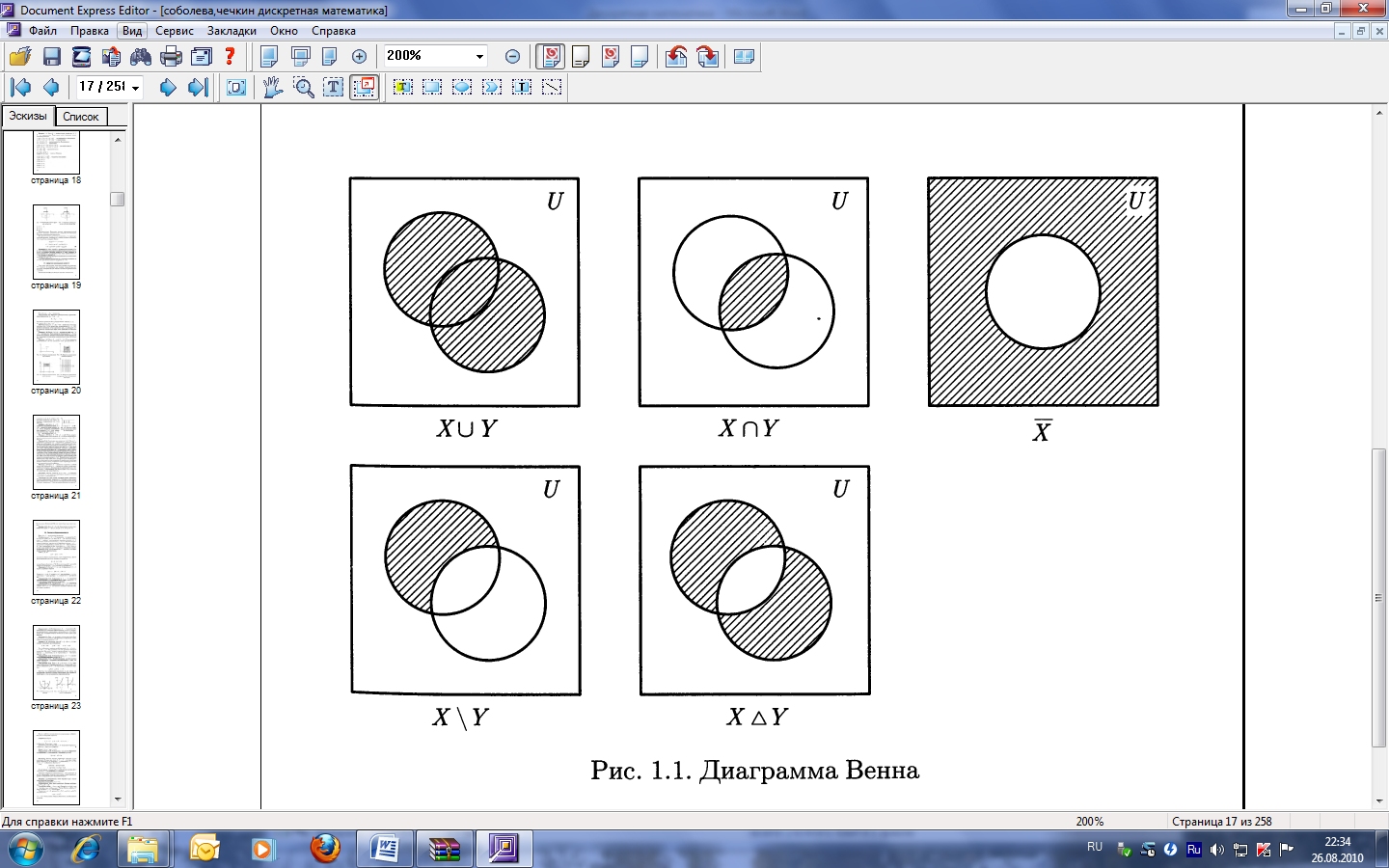
Рис. 1. Диаграммы Венна
-
Теоретико-множественные тождества
Пусть
– универсальное множество, а
– его подмножества. Тогда имеют место
следующие тождественные равенства.
ассоциативность
объединения и пересечения.
коммутативность
объединения и пересечения.
дистрибутивность.
идемпотентность.
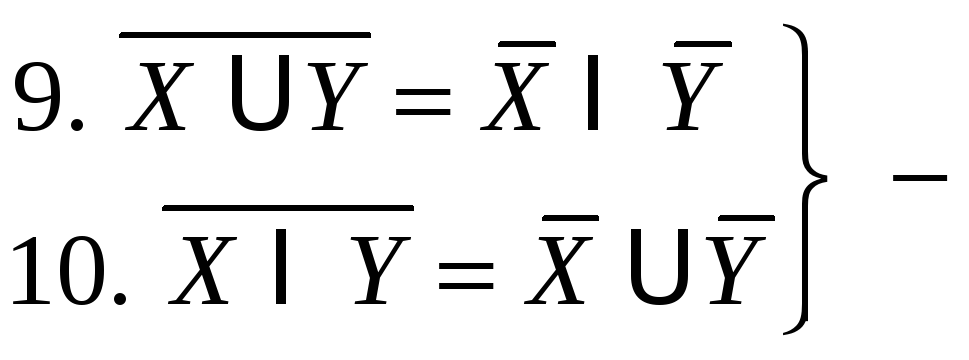законы
де Моргана.
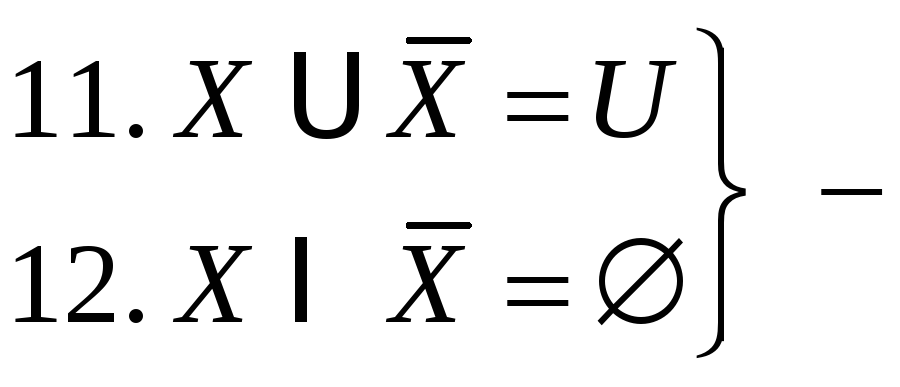дополнимость.
13.
– закон двойного дополнения.
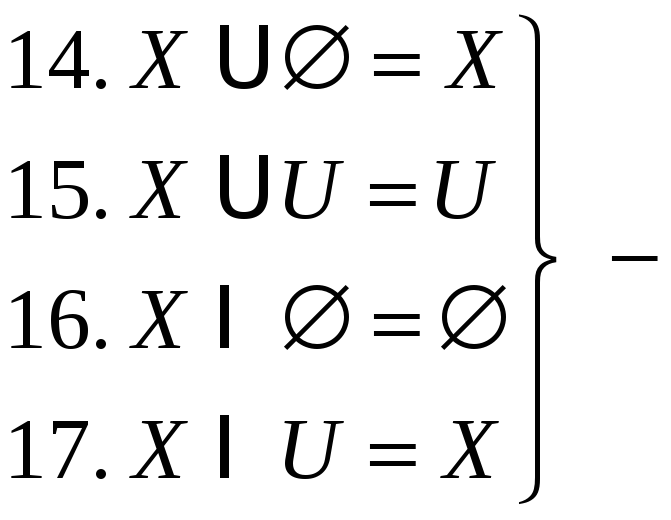существование
универсальных границ.
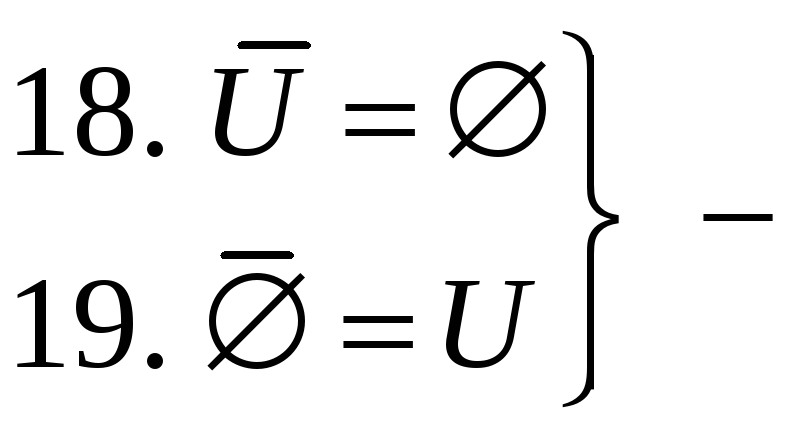законы
дополнения.
Приведенная система тождеств является полной в том смысле, что любое соотношение между множествами является следствием этих тождеств: Справедливость равенств 1 – 19 можно установить, используя принцип равнообъёмности, согласно которому нужно доказать, что множества, стоящие в левой и правой частях равенства состоят из одних и тех же элементов. В качестве примера приведем доказательство равенства 9. Остальные тождества доказываются аналогично. Имеем:
-
Прямое произведение множеств
Прямым
произведением
множеств
и
называют
множество
,
элементами которого являются всевозможные
упорядоченные пары
,
такие, что
,
:
Эта операция над множествами, в отличие от рассмотренных ранее, изменяет природу элементов: в новом множестве элементами являются пары.
Прямое
произведение в общем случае не обладает
свойствами коммутативности и
ассоциативности:
,
.
Пусть
теперь даны
множеств:
.
Упорядоченный набор из
элементов, таких, что
,
,…,
,
называется вектором
или
кортежем.
Множество таких векторов представляет
собой прямое произведение множеств
:
Если
,
то множество
называется степенью
(прямой) множества
и обозначается через
.
Проекцией
вектора
на
-ю
ось (обозначение
)
называется его
компонента. Проекцией вектора
на оси с номерами
называется вектор
длины
(обозначение
).
Пусть
– множество векторов одинаковой длины.
Тогда проекцией множества
на
-ю
ось называется множество проекций всех
векторов на
-ю
ось:
.
Аналогично определяется проекция
множества
на несколько осей:
.
Пример
1.
Пусть
.Тогда
прямым произведением
является множество точек плоскости, то
есть пар вида
,
где
и являются координатами точек плоскости.
Координатное представление точек плоскости, предложенное французским математиком и философом Р. Декартом, является исторически первым примером прямого произведения. Потому прямое произведение называют также декартовым.
Пример
2.
Пусть
,
.
Тогда
– множество, содержащее обозначения
всех 64 клеток шахматной доски.