LK / Лекция 2

Баранов Виктор Павлович. Дискретная математика. Раздел 1. Элементы теории множеств.

Лекция 2. Соответствия, отображения, отношения

Лекция 2. СООТВЕТСТВИЯ, ОТОБРАЖЕНИЯ, ОТНОШЕНИЯ

План лекции:

1. Соответствие между множествами.

2. Понятие отображения множеств.

3. Отношения на множестве.

1. Соответствие между множествами

Соответствием между множествами и называется подмножество . Если , то говорят, что соответствует при соответствии . Множество называется областью определения, а множество – областью значений соответствия. Если , то соответствие называется всюду определенным или полностью определенным (в противном случае – частичным); если , то соответствие называется сюръективным или сюръекцией.

Множество всех , соответствующих элементу , называется образом в при соответствии . Множество всех , которым соответствует элемент , называется прообразом в при соответствии .

Соответствие называется инъективным или инъекцией, если прообразом любого элемента из является единственный элемент из . Соответствие называется функциональным или однозначным, если образом любого элемента из является единственный элемент из . Соответствие называется взаимно однозначным или биекцией, если оно всюду определено, сюръективно, функционально и инъективно.

2. Понятие отображения множеств

Отображением множества во множество называется функциональное соответствие (обозначение ). Множество называется областью определения отображения, элемент – аргументом отображения, элемент – образом при отображении . При этом пишут . Часто, когда множества – числовые, отображение называют функцией. Если числовое только множество , то отображение называют функционалом.

Образом подмножества при отображении называется множество

.

Прообразом подмножества при отображении называется множество

.

По аналогии с соответствиями различают сюръективные, инъективные и биективные отображения.

Пример 1. Обозначим через . Рассмотрим следующие три отображения

,

которые зададим одной формулой: . Они различны, так как различны исходные множества. При этом является сюръективным, но не инъективным; – инъективно, но не сюръективно; – биективно.

Отображения вида называются преобразованиями множества . Преобразование называется тождественным, если .

Пусть и – некоторые отображения. Суперпозицией этих отображений называется отображение , определяемое следующим образом:

.

Отметим, что суперпозиция определена не для любых пар отображений. Однако суперпозиция двух преобразований одного и того же множества определена всегда.

Операция суперпозиции ассоциативна: , где , , – отображения.

Пусть и . Отображение называется обратным к отображению (а отображение обратным к ), если

, .

Обратное отображение обозначается . Если обратное отображение существует, то оно единственно. Необходимое и достаточное условие существования обратного отображения дает следующая теорема.

Теорема 1. Отображение имеет обратное тогда и только тогда, когда оно биективно.

Доказательство. Пусть .

Необходимость. Пусть существует обратное отображение . Рассмотрим и . Тогда , где – прообраз при отображении . Таким образом имеет прообраз , т. е. сюръективно.

Далее, если , причем , то . Следовательно, , т. е. и инъективно. Отсюда биективно, и необходимость доказана.

Достаточность. Пусть биективно. Определим отображение следующим образом. Положим , если . В силу биективности отображение определено на всем , и .

3. Отношения на множестве

Бинарным отношением на множестве называется подмножество . Тот факт, что находится в отношении с , обозначается следующим образом:

Областью определения бинарного отношения на множестве называется множество

,

а областью значений – множество

.

Пример 2. Примеры отношений:

– отношение равенства «=» на множестве состоит из всех пар вида , Если элемент находится в отношении равенства к элементу , то пишут ;

– отношение неравенства «» на множестве R: ;

– отношение делимости «|»на множестве : .

Так как отношения определяются как подмножества, то над ними можно производить теоретико-множественные операции.

Дополнением бинарного отношения на множестве считается множество

.

Например, если – отношение «=», то =«», а «».

Обратным отношением (обращением) для бинарного отношения называется множество

.

Произведением отношений и называется отношение

.

Всякое подмножество называют -местным отношением на множестве .

Совокупность всех отношений на множестве , для которых заданы операции суммы, произведения, разности, дополнения и обращения, образуют алгебру отношений (исчисление отношений) множества . В частности, последняя находит применение при разработке реляционных баз данных.

Свойства отношений. Отношения делятся на различные виды в зависимости от того, обладают или не обладают некоторыми свойствами.

1. Рефлексивность: . Например, рефлексивно на множестве прямых отношение «прямая 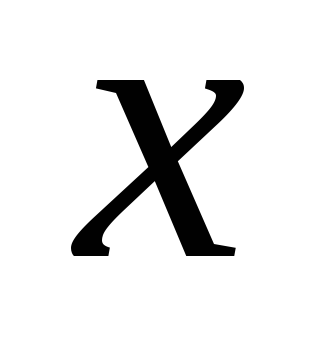пересекает прямую ».

2. Симметричность: . Например, симметрично отношение параллельности на множестве прямых плоскости.

3. Транзитивность: . Например, транзитивно на множестве отрезков отношение «отрезок 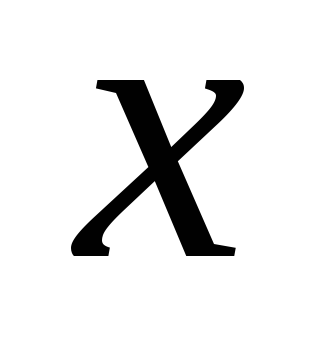длиннее отрезка ».

Среди различных бинарных отношений выделяются два специальных типа, играющих важную роль в разнообразных математических конструкциях и доказательствах.

Отношение эквивалентности. Отношение на множестве называется отношением эквивалентности, если оно обладает свойствами рефлексивности, симметричности и транзитивности. Отношение эквивалентности часто обозначают: .

Пример 3. Примеры отношения эквивалентности:

– отношение «одного роста» на множестве людей;

– отношение подобия на множестве треугольников;

– отношение принадлежности двух студентов к одной студенческой группе.

Смежным классом (классом эквивалентности) элемента по эквивалентности называется множество

.

Любой элемент называется представителем этого класса.

Множество классов эквивалентности элементов множества по эквивалентности называется фактор-множеством по и обозначается .

С каждым отношением эквивалентности связано разбиение множества на непересекающиеся подмножества, которое лежит в основе всевозможных классификаций.

Разбиением множества называется всякое представление этого множества в виде суммы непересекающихся подмножеств:

, .

Здесь – множество индексов, которое может быть конечным, счетным или несчетным. Множества называют слоями разбиения.

Имеет место следующая теорема.

Теорема 2. Для того чтобы отношение позволяло разбить множество на классы, необходимо и достаточно, чтобы было отношением эквивалентности.

Пример 4. Плоскость разбита на прямые

.

Этому разбиению соответствует отношение такое, что если .

Покажем, что каждая эквивалентность отвечает некоторому разбиению множества .

Для каждого обозначим через класс всех элементов, эквивалентных :

.

Из рефлексивности следует, что . Далее, если , то есть , то . Из транзитивности имеем, что , то есть . Таким образом, . В силу симметричности отношения , то есть . Повторяя рассуждения, получим, что . Следовательно, . Таким образом, каждый элемент входит в некоторый класс и различные классы не пересекаются, то есть классы образуют разбиение множества , отвечающее отношению эквивалентности .

Приведем примеры использования отношения эквивалентности для образования математических понятий.

1. Понятие вектора. Сначала вводится понятие направленного отрезка, как пары точек . Два отрезка и объявляются эквивалентными, если середины отрезков и совпадают. Далее проверяется, что это отношение между направленными отрезками рефлексивно, симметрично и транзитивно. Класс эквивалентных отрезков и есть вектор.

2. Построение рациональных чисел из целых. Рассмотрим всевозможные пары из целых чисел такие, что . Пары и объявляются эквивалентными, если 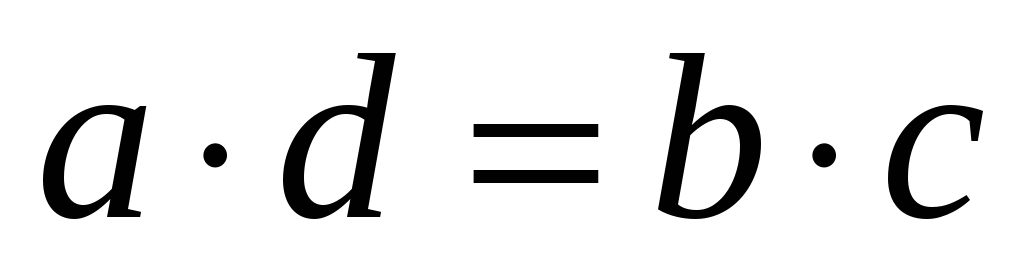. Далее проверяется рефлексивность, симметричность и транзитивность. Класс эквивалентных пар – рациональное число.

Отношение порядка. Бинарное отношение на множестве называется отношением порядка, если оно рефлексивно, транзитивно и антисимметрично. Последнее свойство означает: .

Пример 5. Примеры отношений порядка:

– отношение «» на множестве действительных чисел. Отношение «» порядком не является, так как оно не рефлексивно;

– отношение «» на множестве подмножеств некоторого множества;

– на множестве двоичных слов длины можно ввести отношение порядка следующим образом. Пусть и – двоичные слова. Положим , если для , 1, 2, …, .

Пусть – отношение порядка на множестве . Элементы называются сравнимыми, если или , в противном случае – несравнимыми.

Порядок называется линейным, если любые два элемента сравнимы. В противном случае говорят о частичном порядке. Множество с заданным на нем порядком (частичным или линейным) называется упорядоченным (частично или линейно). Первое отношение в примере 5 задает линейный порядок, два других отношения порядка – частичные. Например, двоичные слова 011 и 110 несравнимы.

Элемент частично упорядоченного множества называется максимальным (минимальным), если из того, что следует . Элемент называется наибольшим (наименьшим), если () для всех .

Верхней (нижней) гранью подмножества частично упорядоченного множества называется такой элемент , что

().

Точной верхней (нижней) гранью подмножества называется наименьшая верхняя (наибольшая нижняя) грань для . Точная верхняя и точная нижняя грани обозначаются соответственно и .

Линейный порядок на множестве называется полным, если каждое непустое подмножество множества имеет наименьший элемент. В этом случае множество называется вполне упорядоченным.