LK / Лекция 15

Баранов Виктор Павлович. Дискретная математика. Раздел 3. Графы и сети.

Лекция 15. Теорема Кёнига-Эгервари

Лекция 15. ТЕОРЕМА КЁНИГА-ЭГЕРВАРИ

План лекции:

1. Понятие трансверсали и покрывающего множества. Словарный ранг матрицы.

2. Теорема Кёнига-Эгервари.

3. Алгоритм построения максимального независимого множества

1. Понятие трансверсали и покрывающего множества. Словарный ранг

матрицы

Теорема Кёнига-Эгервари (1931 г.) вытекает из теоремы Форда-Фалкерсона для транспортных сетей. Она является частным случаем теоремы о различных представителях в теории графов.

Пусть . Совокупность элементов множества называется системой различных представителей семейства множеств или трансверсалью, если выполняются два условия:

1. : ;

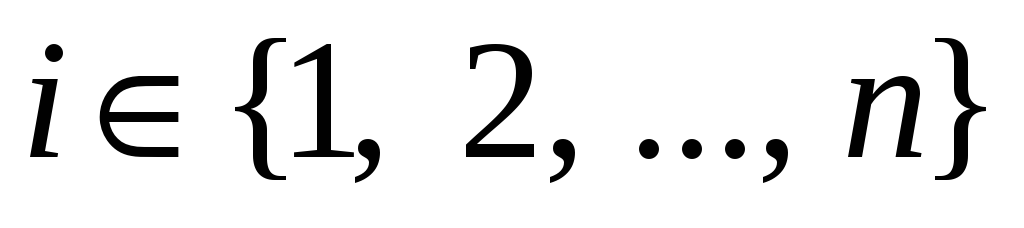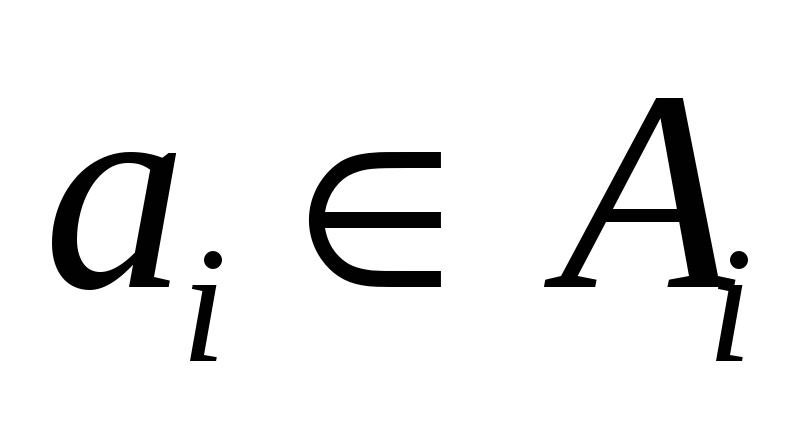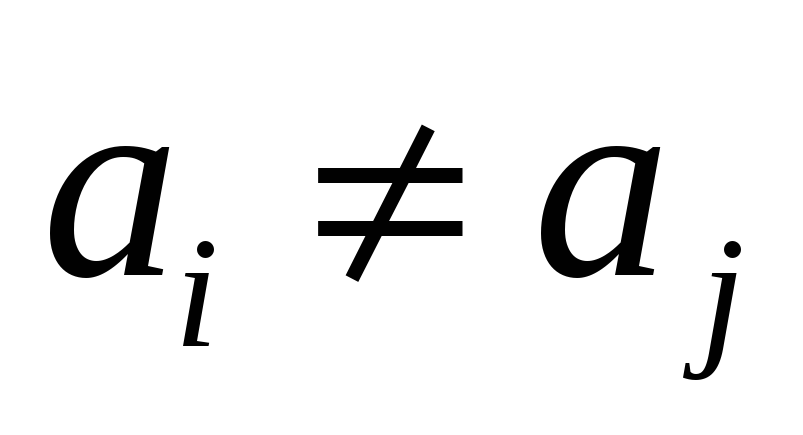2. , если .

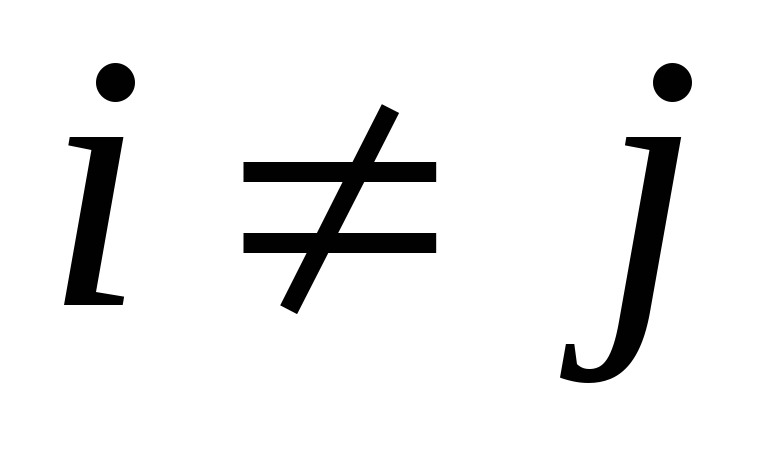Один из подходов к изучению трансверсалей состоит в исследовании так называемой (0,1)-матрицы, то есть матрицы произвольного размера [], составленной из 0 и 1:

, , .

Элементы такой матрицы интерпретируют как разрешенные () и запрещенные ().

Множество разрешенных элементов называется независимым, если эти элементы расположены в различных строках и столбцах, то есть множество

независимо, если

1. ;

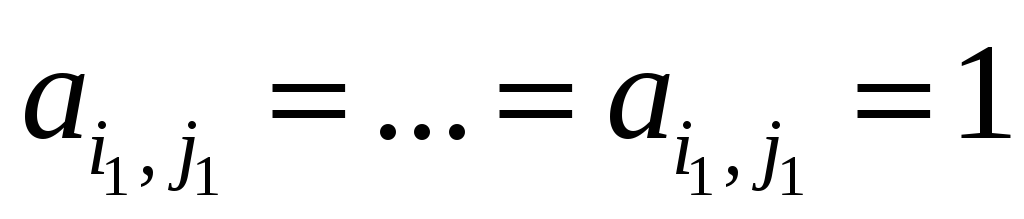2. при , .

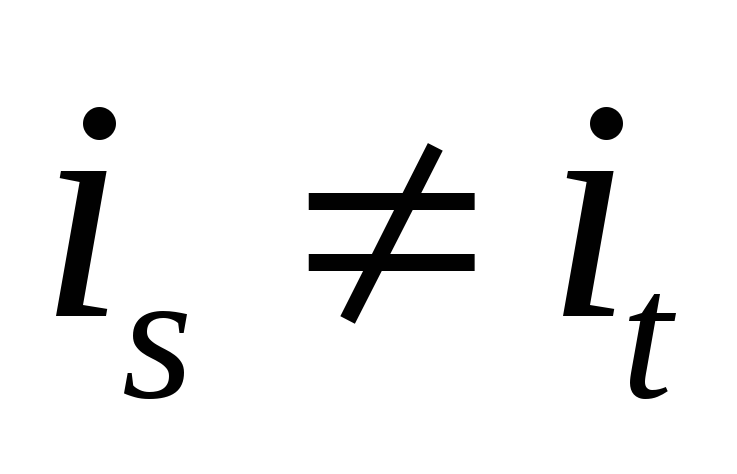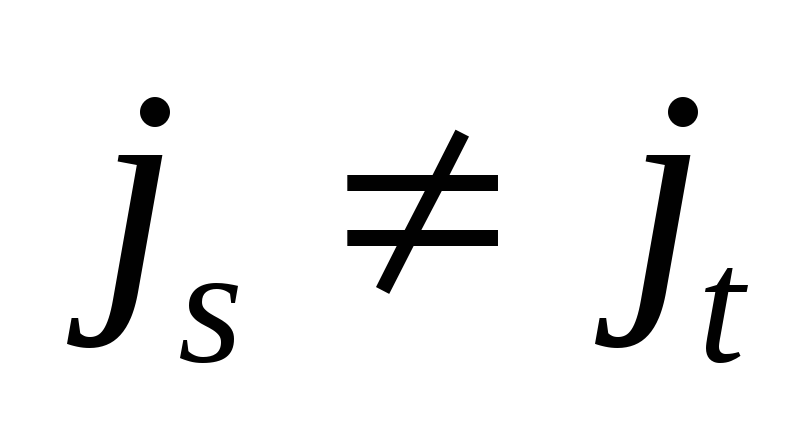Наибольшее число разрешенных элементов в матрице называется словарным рангом.

Будем называть строки и столбцы матрицы рядами или линиями. Совокупность строк и столбцов матрицы, для которой каждый единичный элемент попадает в какой-либо ряд, образуют покрывающее множество, то есть множество

покрывающее, если

или .

Для любых независимых множеств элементов и покрывающих множеств рядов выполняется условие

,

т.к. в независимое множество может входить не более одного элемента из каждого ряда.

2. Теорема Кёнига-Эгервари

Теорема. Словарный ранг (0, 1)-матрицы равен минимальному числу рядов в покрывающем множестве.

Доказательство. Для данной (0,1)-матрицы размера [] построим транспортную сеть следующим образом:

Вершины:

источник и сток ;

вершины-строки – по одной для каждой строки матрицы;

вершины-столбцы – по одной для каждого столбца матрицы.

Дуги:

источник соединен дугой с каждой вершиной-строкой;

сток соединен дугой с каждой вершиной-столбцом;

вершина-строка соединяется дугой с вершиной-столбцом в том и только том случае, когда .

Пропускные способности:

пропускные способности каждой дуги равна 1.

Решим для построенной сети задачу о максимальном потоке, применяя алгоритм расстановки отметок. Предположим, что построен максимальный поток, то есть процесс расстановки отметок закончился, но сток не получил отметки. Обозначим величину максимального потока через .

Из определения потока следует, что на любой дуге он не превышает ее пропускной способности, то есть может равняться 0 или 1. Пусть

(1)

все дуги в «средней» части сети (без дуг, выходящих из источника, и дуг, входящих в сток), поток по которым равен 1. Из уравнения сохранения потока следует, что

есть независимое множество элементов матрицы. Действительно, каждая вершина-строка, по построению сети, имеет только одну входящую дугу (от источника), поэтому для каждой такой вершины сумма значений потока по дугам, входящим в вершину, равна 0 или 1. Следовательно, и сумма значений потока по дугам, выходящим из вершины, также не превышает 1. Значит, для каждой вершины-строки из (1) поток равен 1 только на одной из выходящих из этой вершины дуг, поэтому все индексы различны. Аналогичные рассуждения имеют место для индексов .

Из уравнения сохранения для источника и стока имеем, что поток на дугах

равен 1, а на остальных дугах в «средней» части сети поток равен нулю.

Рассмотрим процедуру отметки вершин сети.

На первом шаге алгоритма при просмотре вершины все вершины-строки, входящие в множество , отметку не получат, так как поток по дугам, идущим из в эти вершины равен 1, то есть пропускной способности дуги. Все остальные вершины- строки получат отметку , так как поток по дугам, идущим в них от источника, равен 0.

На втором шаге алгоритма в результате просмотра на первом шаге вершин-строк будут помечены вершины-столбцы, в которые ведут из них дуги. В силу максимальности потока, помеченным может оказаться только какой-либо столбец из множества , так как в противном случае происходит «прорыв» в вершину и возможность увеличения потока, что противоречит максимальности ранее найденного потока.

На третьем шаге при просмотре помеченной вершины-столбца пометку может получить только одна вершина-строка , так как из всех дуг, входящих в вершину , только по дуге поток больше 0 (равен 1).

Пусть – множество номеров непомеченных строк, а – множество номеров помеченных столбцов. Из предыдущих рассуждений следует, что

, ,

причем вершина-строка является помеченной в том и только в том случае, когда помечена вершина-столбец . Другими словами, в паре либо обе вершины помечены, либо обе не помечены. Отсюда

. (2)

Так как процесс расстановки отметок остановился, то в «средней» части сети нет дуг, у которых начало помечено, а конец не помечен (это возможно только в вершине-стоке или вершине-источнике). Следовательно, каждая дуга либо имеет начало в множестве , либо конец в множестве , то есть покрывающее множество рядов . Тогда

.

Таким образом, построено независимое множество элементов и покрывающее множество рядов с одинаковым числом элементов. Теорема доказана.

3. Алгоритм построения максимального независимого множества

Рассмотрим алгоритм построения максимального потока для указанной выше сети как последовательность действий непосредственно с заданной (0,1)-матрицей, то есть не строя сеть фактически.

Сначала построим какое-нибудь независимое множество элементов. Можно, например, просматривать столбцы по порядку и в каждом находить первый попавшийся единичный элемент. Найденный элемент зачисляется в независимое множество, а строка и столбец, в которых он находится, вычеркиваются из матрицы. Если в каком либо столбце нет единичных элементов, то переходим к следующему.

Пусть на этом шаге построено независимое множество

. (3)

Если (в каждой строке выбран какой-то элемент) или (в каждом столбце выбран какой-то элемент), то, очевидно, построено максимальное независимое множество и алгоритм закончен.

В противном случае начинаем процесс расстановки отметок, позволяющий либо увеличить независимое множество (3), либо убедиться, что оно максимальное.

Пометим каким-то образом, например, звездочкой «пустые» строки, то есть строки, в которых нет элемента, входящих в независимое множество (3). Далее, как в общем алгоритме, выполняем циклически шаги просмотра вершин, то есть строк и столбцов. После каждого шага ряды матрицы делятся на три группы: непомеченные, помеченные и не просмотренные, помеченные и просмотренные. Ряды из последней группы в последующих шагах не участвуют.

Описание шага алгоритма. Берем очередной помеченный, но не просмотренный ряд. Если этим рядом является строка с номером , то помечаем отметкой все непомеченные столбцы, имеющие 1 в данной строке. Если этим рядом является столбец с номером , то находим в независимом множестве элемент и помечаем отметкой строку .

Имеется два варианта остановки описанного процесса.

1. При просмотре столбца в нем оказался разрешенный элемент, не входящий в текущее независимое множество . Пусть

– номер такого столбца;

– отметка столбца ;

– отметка строки ; (то есть )

– отметка столбца ;

– отметка строки ; (то есть )

…

– отметка строки ;

– отметка столбца ,

где строка помечена звездочкой. Тогда элементы

в независимом множестве можно заменить на элементы

,

увеличив на 1 число независимых элементов.

2. Просмотрены все ряды, то есть помеченных и не просмотренных рядов больше нет. В этом случае совокупность помеченных столбцов и не помеченных строк образует покрывающее множество рядов. Число рядов равно числу элементов в независимом множестве, откуда по теореме Кёнига-Эгервари следует, что оно максимально.

Пример. Определить словарный ранг матрицы

.

4