
LK / Лекция 22
.docБаранов Виктор Павлович. Дискретная математика.
Раздел 4. Функциональные системы с операциями. Алгебра логики.
Лекция 22. Полнота и замкнутость. Полином Жегалкина

Лекция 22. ПОЛНОТА И ЗАМКНУТОСТЬ. ПОЛИНОМ ЖЕГАЛКИНА
План лекции:
-
Полнота и замкнутость. Примеры функционально полных систем.
-
Представление булевых функций полиномом Жегалкина.
-
Полнота и замкнутость. Примеры функционально полных систем
Система функций
![]() из
из
![]() называется функционально полной,
если любая булева функция может быть
представлена в виде формулы через
функции этой системы.
называется функционально полной,
если любая булева функция может быть
представлена в виде формулы через
функции этой системы.
Примеры полных систем.
-
Система
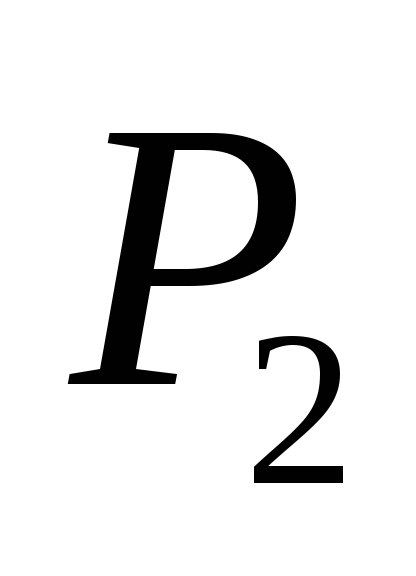 – множество всех булевых функций.
– множество всех булевых функций. -
Система
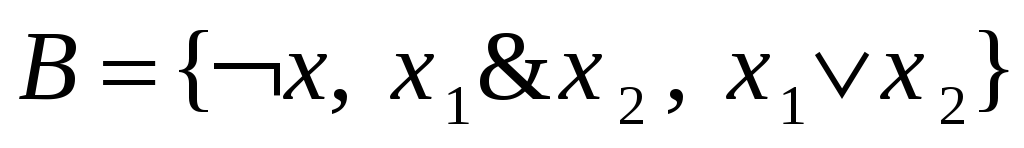
Очевидно, что не каждая система является
полной, например, система
![]() не полная. Следующая теорема позволяет
сводить вопрос о полноте одних систем
к вопросу о полноте других систем.
не полная. Следующая теорема позволяет
сводить вопрос о полноте одних систем
к вопросу о полноте других систем.
Теорема. Пусть
даны две системы функций из
![]() :
:
![]() ,
,
![]() ,
,
относительно которых известно, что
система
![]() полна и каждая ее функция выражается в
виде формулы через функции системы
полна и каждая ее функция выражается в
виде формулы через функции системы
![]() .
Тогда система
.
Тогда система
![]() является полной.
является полной.
Доказательство.
Пусть
![]() –
произвольная функция из
–
произвольная функция из
![]() .
В силу полноты системы
.
В силу полноты системы
![]() можно выразить
можно выразить
![]() формулой над
формулой над
![]() ,
т. е.
,
т. е.
![]() .
.
По условию теоремы
![]() ,
,
![]() ,
…,
,
…,
![]() .
.
Поэтому в формуле
![]() можно исключить вхождения функций
можно исключить вхождения функций
![]() ,
заменив их формулами над
,
заменив их формулами над
![]() :
:
![]() ,
,
То есть мы выразили
![]() в виде формулы над
в виде формулы над
![]() .
Теорема доказана.
.
Теорема доказана.
Опираясь на эту теорему, можно установить полноту еще ряда систем и тем самым расширить список примеров полных систем.
-
Система
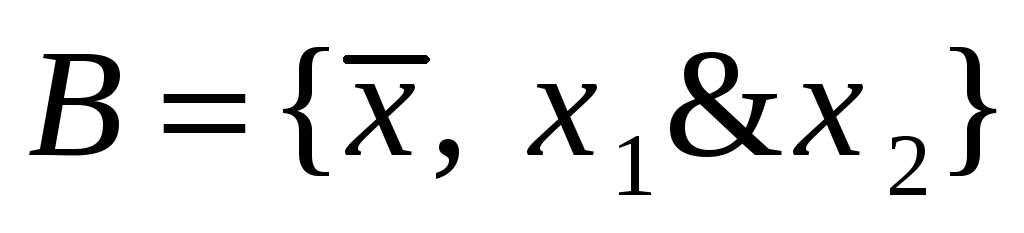 является полной. Для доказательства
возьмем за систему
является полной. Для доказательства
возьмем за систему
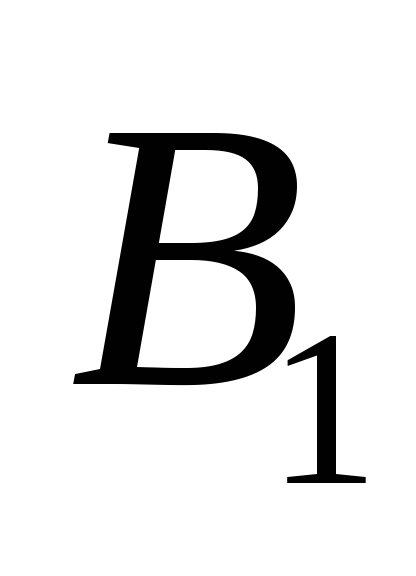 систему 2), а за систему
систему 2), а за систему
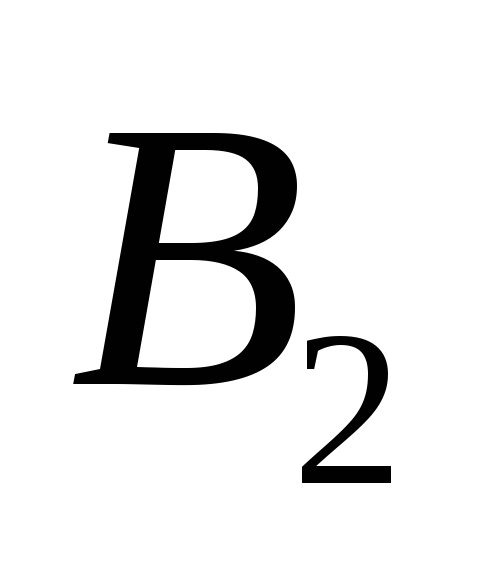 – систему 3) и используем тождество
– систему 3) и используем тождество
![]() .
.
-
Система
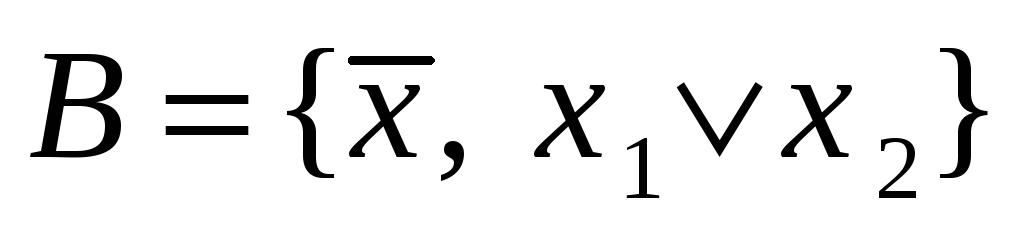 является полной. Доказательство
аналогично предыдущему, либо через
принцип двойственности.
является полной. Доказательство
аналогично предыдущему, либо через
принцип двойственности. -
Система
 является полной. Для доказательства
возьмем за систему
является полной. Для доказательства
возьмем за систему
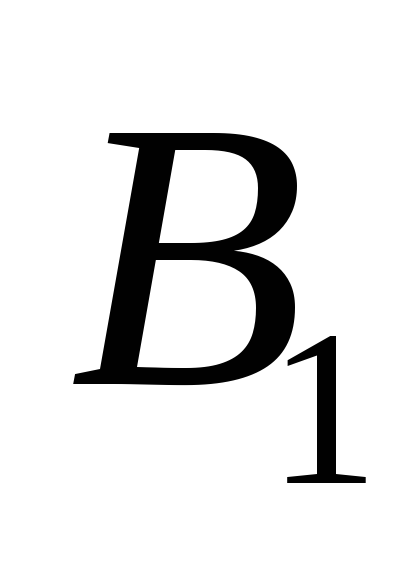 систему 3), а за систему
систему 3), а за систему
 – систему 5). Тогда
– систему 5). Тогда
![]() ,
,
![]() .
.
-
Система
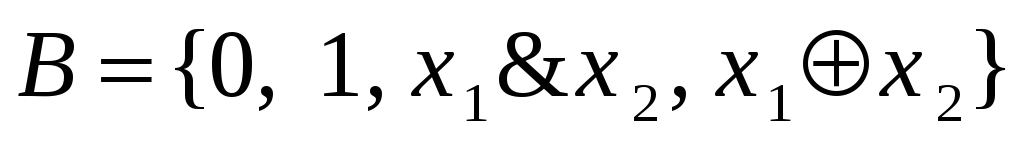 является полной. Для доказательства
возьмем за систему
является полной. Для доказательства
возьмем за систему
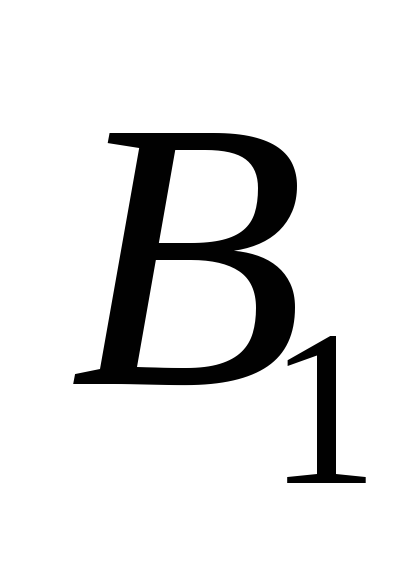 систему 3), а за систему
систему 3), а за систему
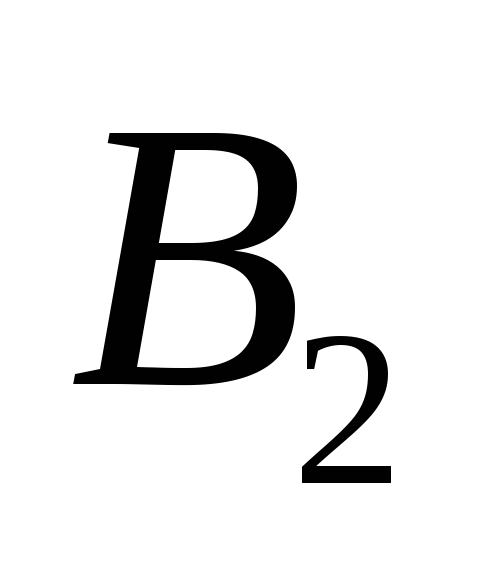 – систему 6). Имеем
– систему 6). Имеем
![]() .
.
С понятием полноты тесно связано понятие замыкания и замкнутого класса.
Пусть
![]() – некоторое подмножество функций из
– некоторое подмножество функций из
![]() .
Замыканием
.
Замыканием
![]() называется множество всех булевых
функций, представимых в виде формул
через функции множества
называется множество всех булевых
функций, представимых в виде формул
через функции множества
![]() .
Замыкание множества
.
Замыкание множества
![]() обозначается через
обозначается через
![]() .
Очевидно, что замыкание инвариантно
относительно операций введения и
удаления фиктивных переменных.
.
Очевидно, что замыкание инвариантно
относительно операций введения и
удаления фиктивных переменных.
Свойства замыкания:
-
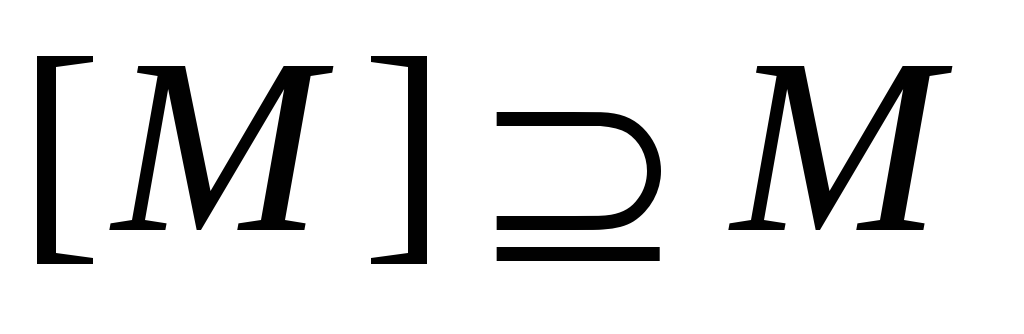 ;
; -
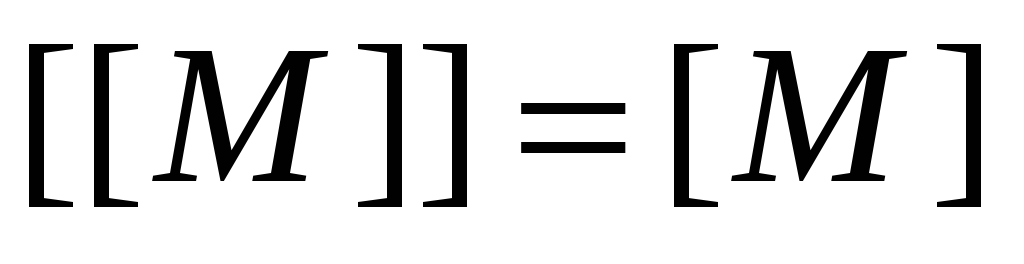 ;
; -
если
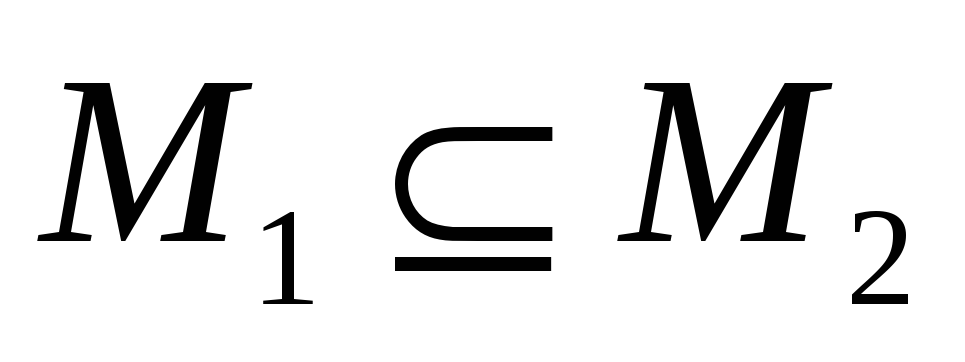 ,
то
,
то
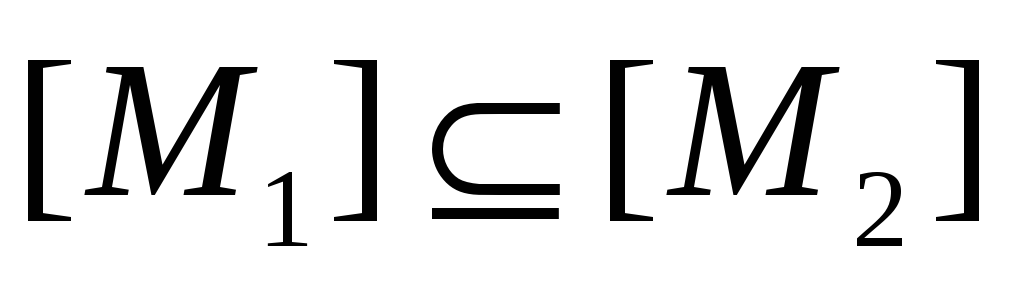 ;
; -
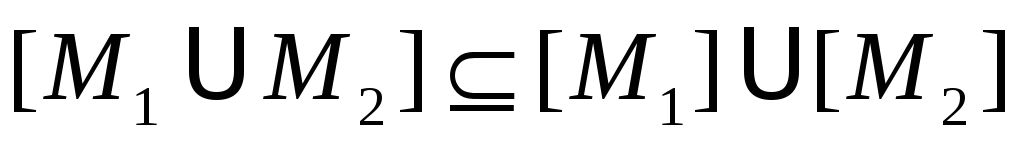 .
.
Класс (множество)
![]() называется функционально замкнутым,
если
называется функционально замкнутым,
если
![]() .
.
Очевидно, что всякий класс
![]() будет замкнутым.Это дает возможность
получать многочисленные применения
замкнутых классов.
будет замкнутым.Это дает возможность
получать многочисленные применения
замкнутых классов.
В терминах замыкания и замкнутого класса
можно дать другое определение полноты,
эквивалентное исходному:
![]() – полная система, если
– полная система, если
![]() .
.
-
Представление булевых функций полиномом Жегалкина
Рассмотрим полную систему функций
![]() .
Формула, построенная из функций этой
системы, после раскрытия скобок и
алгебраических преобразований переходит
в полином по mod 2, который
в честь русского логика конца XIX
века И.И. Жегалкина называют полиномом
Жегалкина. Возможность такого
преобразования следует из следующих
тождеств:
.
Формула, построенная из функций этой
системы, после раскрытия скобок и
алгебраических преобразований переходит
в полином по mod 2, который
в честь русского логика конца XIX
века И.И. Жегалкина называют полиномом
Жегалкина. Возможность такого
преобразования следует из следующих
тождеств:
![]() ;
(1)
;
(1)
![]() ;
(2)
;
(2)
![]() ;
(3)
;
(3)
![]() ;
(4)
;
(4)
![]() .
(5)
.
(5)
Действительно, из тождеств (1) – (5)
следует, что формулы, содержащие операции
& и
![]() ,
можно преобразовывать по обычным
алгебраическим законам: переставлять
слагаемые и множители, раскрывать
скобки, выносить общий множитель за
скобки.
,
можно преобразовывать по обычным
алгебраическим законам: переставлять
слагаемые и множители, раскрывать
скобки, выносить общий множитель за
скобки.
Пример 1. Представим функцию
![]() над множеством связок
над множеством связок
![]() :
:
![]() .
(6)
.
(6)
Рассмотрим произвольную булеву функцию
![]() .
Представим ее формулой в базисе
.
Представим ее формулой в базисе
![]() ,
например, совершенной д. н. ф., после чего
заменим в этой формуле каждую операцию
,
например, совершенной д. н. ф., после чего
заменим в этой формуле каждую операцию
![]() по формуле (6), а каждое отрицание по
формуле
по формуле (6), а каждое отрицание по
формуле
![]() .
В полученном выражении раскроем скобки
и приведем подобные члены. В результате
получим полином
.
В полученном выражении раскроем скобки
и приведем подобные члены. В результате
получим полином
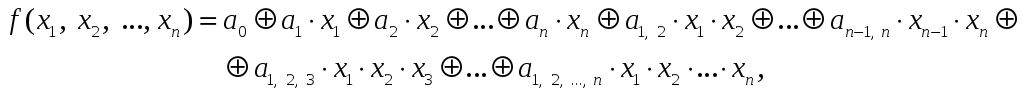
где коэффициенты полинома либо равны 1, либо 0 в зависимости от наличия или отсутствия соответствующего члена.
Приведенное выше рассуждение доказывает справедливость следующей теоремы, принадлежащей И.И. Жегалкину.
Теорема. Каждая
функция из
![]() представима полиномом Жегалкина.
представима полиномом Жегалкина.
Подсчитаем число полиномов Жегалкина
от переменных
![]() ,
то есть число выражений вида
,
то есть число выражений вида
![]() .
.
Число членов
![]() равно количеству подмножеств
равно количеству подмножеств
![]() множества
множества
![]() ,
то есть
,
то есть
![]() .
Поскольку коэффициент
.
Поскольку коэффициент
![]() равен 0 или 1, то искомое число полиномов
равно
равен 0 или 1, то искомое число полиномов
равно
![]() ,
то есть числу всех булевых функций от
тех же переменных. Отсюда, как следствие,
получаем единственность представления
функций полиномом Жегалкина.
,
то есть числу всех булевых функций от
тех же переменных. Отсюда, как следствие,
получаем единственность представления
функций полиномом Жегалкина.
Пример 2. Представить функцию
![]() в виде полинома Жегалкина.
в виде полинома Жегалкина.
Будем искать выражение для данной функции в виде полинома с неопределенными коэффициентами:
![]() .
.
При
![]() имеем
имеем
![]() ,
,
при
![]() имеем
имеем
![]() ,
,
при
![]() имеем
имеем
![]() ,
,
при
![]() имеем
имеем
![]() ,
то есть
,
то есть
![]() .
.
Отсюда
![]() .
.
Пример 2. Представить полиномом Жегалкина функцию, заданную таблицей истинности:
-
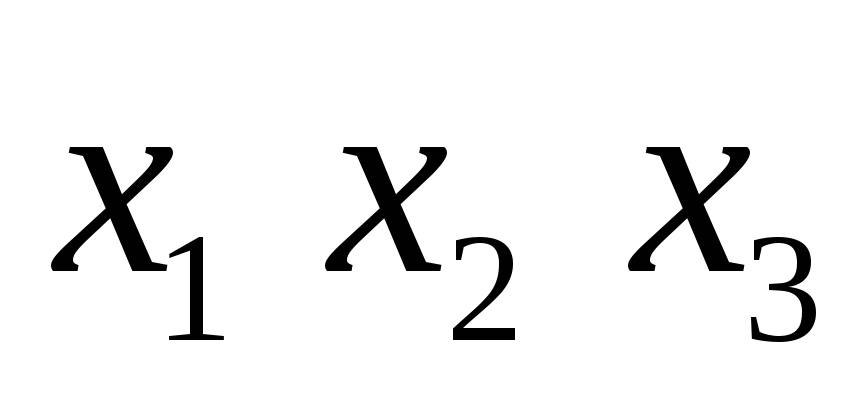
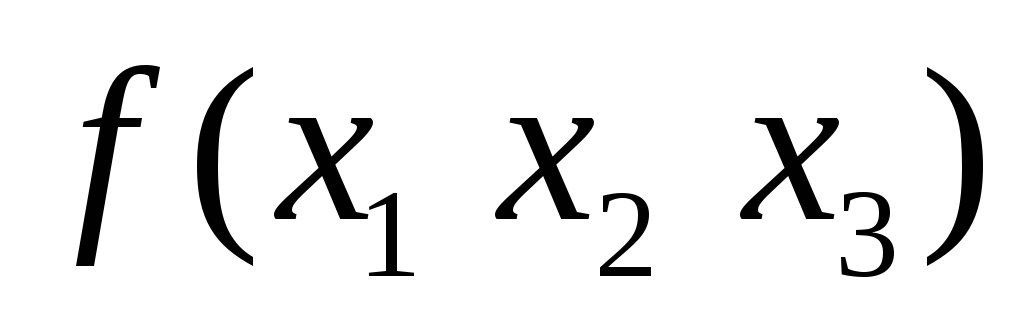
0 0 0
1
0 0 1
0
010
1
011
1
100
0
101
0
110
0
111
1
Рассматриваемый далее алгоритм построения полинома Жегалкина применим для любой булевой функции.
-
Представим заданную функцию совершенной д.н.ф.:
![]() .
(6)
.
(6)
Из формулы
![]() следует, что для булевых функций
следует, что для булевых функций
![]() и
и
![]() ,
одновременно не обращающихся в 1 (
,
одновременно не обращающихся в 1 (![]() ),
выполняется равенство
),
выполняется равенство
![]() .
Такие функции называются ортогональными.
Из последнего равенства следует, что
логическая сумма для ортогональных
слагаемых не изменяется, если операцию
.
Такие функции называются ортогональными.
Из последнего равенства следует, что
логическая сумма для ортогональных
слагаемых не изменяется, если операцию
![]() заменить на
заменить на
![]() .
Далее выполним следующий шаг,
воспользовавшись этим результатом.
.
Далее выполним следующий шаг,
воспользовавшись этим результатом.
-
Заменим в выражении (6) все знаки
 на
на
 :
:
![]() .
.
-
Заменим все отрицания по формуле
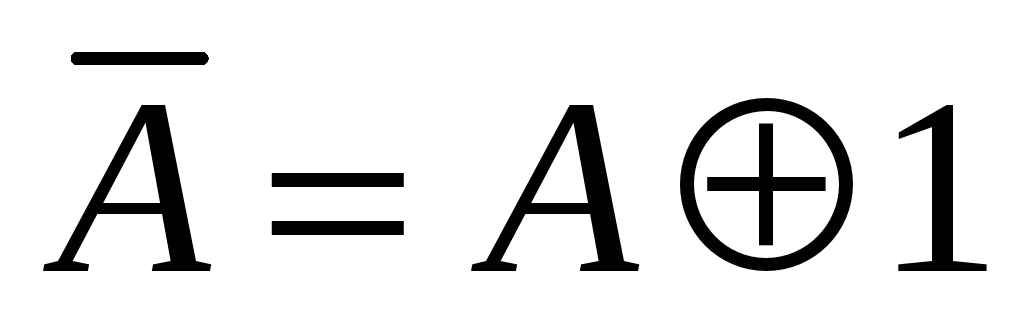 ,
раскроем скобки и приведем подобные
члены:
,
раскроем скобки и приведем подобные
члены:
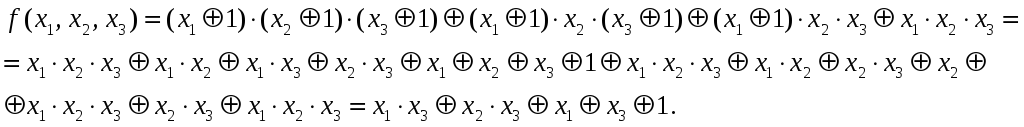
Из приведенных примеров следует, что существует целый ряд полных систем. Таким образом, для задания булевых функций можно использовать различные языки формул. Какой именно из языков является более удобным, зависит от характера рассматриваемой задачи.
