3. Диаметр, радиус и центр графа

Для связного графа определим расстояние между двумя его вершинами и как длину самой короткой цепи, соединяющей эти вершины, и обозначим через . Длина цепи – это количество ребер, составляющих цепь. Нетрудно проверить, что введенное расстояние удовлетворяет аксиомам метрики:

1)

2) ;

3) .

Определим расстояние от каждой вершины графа до самой далекой от нее вершины

,

которое называется эксцентриситетом. Очевидно, что эксцентриситет для всех вершин в полного графа равен единице, а для вершин простого цикла – .

Максимальный эксцентриситет носит название диаметра графа, а минимальный – радиуса графа . В полном графе имеем , а в простом цикле – .

Вершина называется центральной, если . Граф может иметь несколько таких вершин, а в некоторых графах все вершины являются центральными. В простой цепи при нечетном числе вершин только одна является центральной, а при четном их числе таких вершин две. В полном графе и для простого цикла центральными являются все вершины. Множество центральных вершин называется центром графа.

Пример 1. Найти диаметр, радиус и центр графа, приведенного на рис. 4.

° °

° ° °

° °

° °

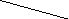
Рис. 4.

Для решения этой задачи удобно предварительно вычислить матрицу расстояний между вершинами графа. В данном случае это будет матрица размером , в которой на месте стоит расстояние от вершины до вершины :

Для каждой строки матрицы находим наибольший элемент и записываем его справа от черточки. Наибольшее из этих чисел равно диаметру графа , наименьшее – радиусу графа . Центр графа составляют центральные вершины и .

Понятия центральной вершины и центра графа появились в связи с задачами оптимального размещения пунктов массового обслуживания, таких как больницы, пожарные части, пункты охраны общественного порядка и т. п., когда важно минимизировать наибольшее расстояние от любой точки некоторой сети до ближайшего пункта обслуживания.

4. Матрицы достижимостей и контрадостижимостей

Матрица достижимостей определяется следующим образом:

Множество вершин графа , достижимых из заданной вершины , состоит из таких элементов , для которых -й элемент в матрице равен 1. Это множество можно представить в виде

.

Матрица контрадостижимостей (обратных достижимостей) определяется следующим образом:

Аналогично построению достижимого множества можно сформировать множество , используя следующее выражение:

.

Из определений следует, что -й столбец матрицы совпадает с -й строкой матрицы , т. е. , где – матрица, транспонированная к матрице .

Пример 2. Найти матрицы достижимостей и контрадостижимостей для графа, приведенного на рис. 5.

°

°

°

°

°

°

°

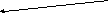Рис. 5.

Определим множества достижимостей для вершин графа:

,

,

,

,

,

,

.

Следовательно, матрицы достижимостей и контрадостижимостей имеют вид:

, .

Так как – множество таких вершин, каждая из которых принадлежит по крайней мере одному пути, идущему от к , то вершины этого множества называются существенными или неотъемлемыми относительно концевых вершин и . Все остальные вершины называются несущественными или избыточными, поскольку их удаление не влияет на пути от к .

Можно определить также матрицы ограниченных достижимостей и контрдостижимостей, если потребовать, чтобы длины путей не превышали некоторого заданного числа. Тогда будет верхней границей длины допустимых путей.

Граф называют транзитивным, если из существования дуг и следует существование дуги . Транзитивным замыканием графа является граф , где – минимально возможное множество дуг, необходимых для того, чтобы граф был транзитивным. Очевидно, что матрица достижимостей графа совпадает с матрицей смежности графа , если в матрице на главной диагонали поставить единицы.

6