3.1 Матричная экспонента

Другой метод решения линейных систем с постоянными коэффициентами основан на использовании в качестве фундаментальной матрицы матричной экспоненты Матрица 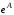определяется как сумма ряда

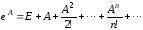
Если матрица 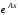найдена, то решение системы (3.1) с начальным условиемимеет вид.

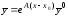Для отыскания матрицы 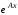могут быть применены различные приемы, в зависимости от структуры спектра матрицы.

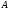1. Если все собственные значения 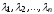матрицы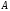– действительные различные числа, то матрицу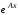удобно находить так:

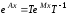, (3.6)

где 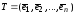(матрица, составленная из столбцов координат собственных векторов матрицы А), а

.

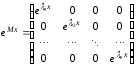2. Если среди различных собственных значений матрицы А имеются комплексные, то матрица 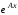в вещественной форме может быть найдена с помощью следующего приема: нужно найти общее решение системы (3.1) так, как это было описано выше, а потом составить матрицу,i-ым столбцом которой будет решение этой системы, удовлетворяющее начальным условиям ,.

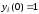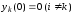Пример 4. Для матрицы системы из примера 2 найти .

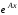Решение. Составим матрицу Т из столбцов координат собственных векторов матрицы А:

.

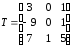Тогда

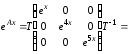
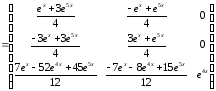
Пример 5. Для матрицы 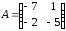найти.

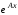Решение. Собственные значения матрицы 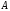– комплексно сопряженные числа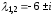. Собственный вектор, соответствующий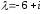

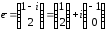
Имеем:

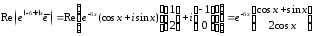
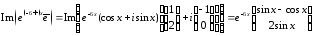
Поэтому общее решение линейной системы (30) с заданной матрицей А имеет вид

.

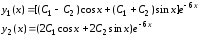Найдем, сначала частное решение, удовлетворяющее условию 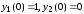. Оно будет иметь вид

.

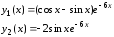Частное решение, удовлетворяющее условиям 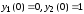, имеет вид

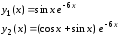
Поэтому

.

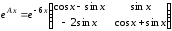3. Если среди собственных значений матрица А имеются кратные, то следует отыскать матрицу 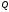, приводящую матрицу А к жордановой форме:

.

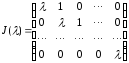
Жорданова клетка 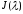, соответствующая корню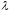кратности, имеет вид

.

Для такой клетки легко находится

. (3.7)

Проведя такие построения для каждой клетки Жордана, находим 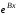. Тогда.

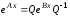Пример 6. Вычислить матрицу 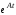, если.

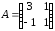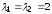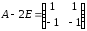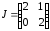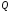Решение. Собственные значения данной матрицы . Так как ранг матрицыравен 1, от жорданова форма матрицы А имеет вид. Матрицу, приводящую матрицу А к жордановой форме, найдем из уравнения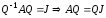. Пусть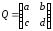. Тогда для отыскания элементов матрицы 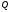получим уравнение

.

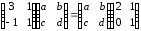Это матричное уравнение эквивалентно системе

,

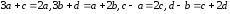решение которой следующее: 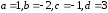. Итак,

.

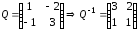Согласно формуле (35) 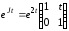. Поэтому

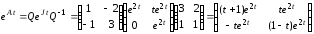(3.8)

3.2. Формула Коши

Решение неоднородной системы с постоянными коэффициентами

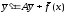, (3.9)

удовлетворяющее начальному условию 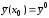, может быть выражено через экспоненциал матрицы системы по формуле

(3.10)

Если решение системы (3.9) записано в виде (3.10), то говорят, что оно записано в форме Коши.

Пример 7. Найдя матрицу 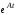, записать решение системы

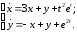
в форме Коши.

Матрица 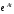для рассматриваемой системы уже была найдена в предыдущем примере, и она имеет вид (3.8). Согласно формуле (3.10), можем записать

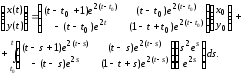
Задание 12

Решить линейную систему путем сведения ее к одному уравнению высшего порядка

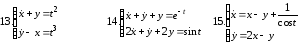
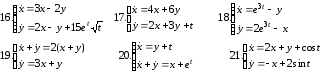
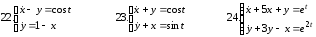
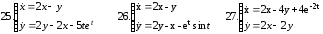
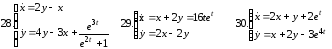
Задание 13

Решить систему матричным методом

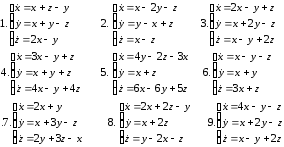
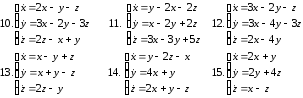
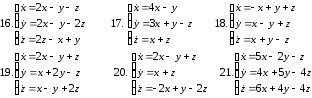
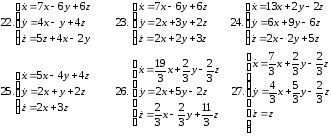
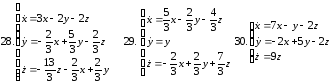
Задание 14

Найт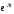и , где А – матрица линейной части системы из задачи 12 и записать решение этой системы по формуле Коши.