Задача 1

ПРИЛОЖЕНИЕ.

Пример 1.

«Расчет переходных процессов в линейных электрических цепях

с сосредоточенными параметрами»

Задача 1 (рис. 1, табл. 2,3)

1. Найти закон изменения во времени переходного тока или переходного напряжения в электрической цепи, схема которой приведена на рис.1, при действии в ней постоянной ЭДС Е=100 В.

Расчет выполнить классическим и операторным методами (при выполнении расчета использовать ЭВМ).

2. Построить в масштабе график переходной величины, найденной в п.1.

Значения R₁, R₂, R₃, C, L, а также определяемая переходная величина указаны в табл.2. Величина R₄ приведена в табл.3.

Рис. 1

Таблица 2

Номер варианта	R1, Ом	R2, Ом	R3, Ом	С, мкФ	L, мГн	Искомая величина
5	0	1000	100	1,43	77,0	uL

Таблица 3

Индекс группы	1
R4, Ом	10

Решение:

1. Классический метод.

Схема исследуемой цепи, согласно заданию:

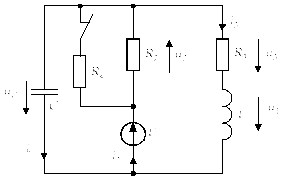
1.1.1 Схема замещения цепи до коммутации при . Т.к. в цепи источник

постоянного напряжения, то индуктивность в установившемся режиме будет представлять собой короткое замыкание, а емкость разрыв ветви. Сопротивления и параллельны, заменим их эквивалентным:

.

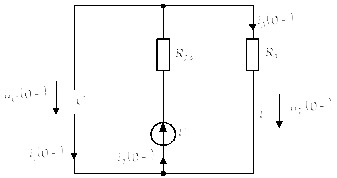
Найдем независимые начальные условия (ННУ), т.е. определим ток через индуктивность и напряжение емкости  в схеме до коммутации .

По второму закону Кирхгофа для контура :

Отсюда:

.

По второму закону Кирхгофа для контура :

Отсюда:

Зависимое начальное условие (ЗНУ):

1.1.2 Цепь при (непосредственно после коммутации).

По законам коммутации:

.

.

Для определения зависимого начального условия нарисуем схему цепи при (непосредственно после коммутации). Начальные условия ненулевые, поэтому индуктивные элементы заменяем источниками тока со значениями , емкостные элементы – источниками ЭДС со значениями .

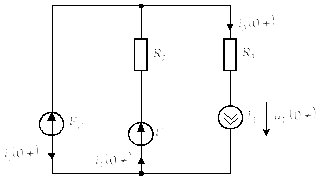
Здесь

.

Для контура по второму закону Кирхгофа:

Отсюда:

1.1.3 Цепь при . Определяем принужденную составляющую.

Здесь также установившийся режим, следовательно, индуктивность представляет собой короткое замыкание, емкость представляет собой разрыв ветви.

По второму закону Кирхгофа:

.

1.1.5 Составим характеристическое уравнение.

Для этого в цепи после коммутации все источники положим равными нулю, и найдем входное сопротивление цепи относительно любой ветви:

.

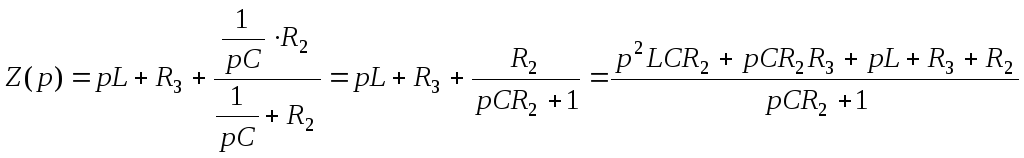Подставляя числовые значения, получим:

Приравняв к нулю, получим корни характеристического уравнения:

.

.

.

Здесь:

- коэффициент затухания переходного процесса;

- частота свободных колебаний.

5. Запишем мгновенное значение тока индуктивности 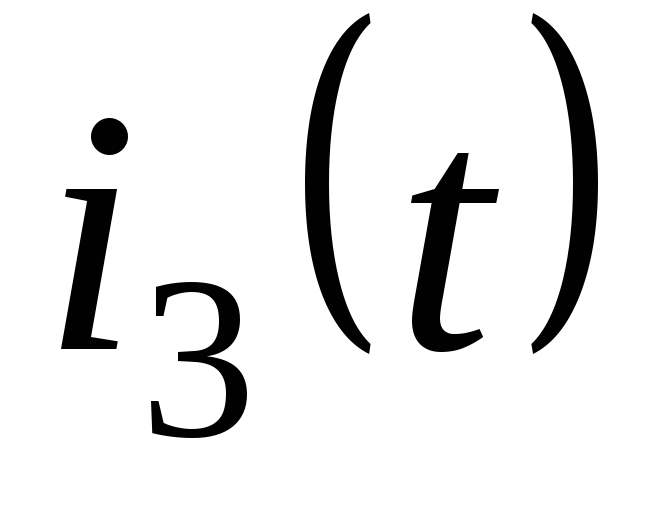в общем виде:

Учитывая, что корни характеристического уравнения комплексно-сопряженные,

переходные процессы в цепи носят колебательный характер.

Подставляем числовые значения:

Продифференцируем:

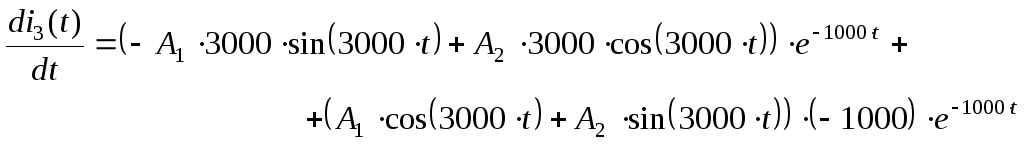
5. Определяем постоянные интегрирования.

При из уравнений получим систему уравнений для тока индуктивности:

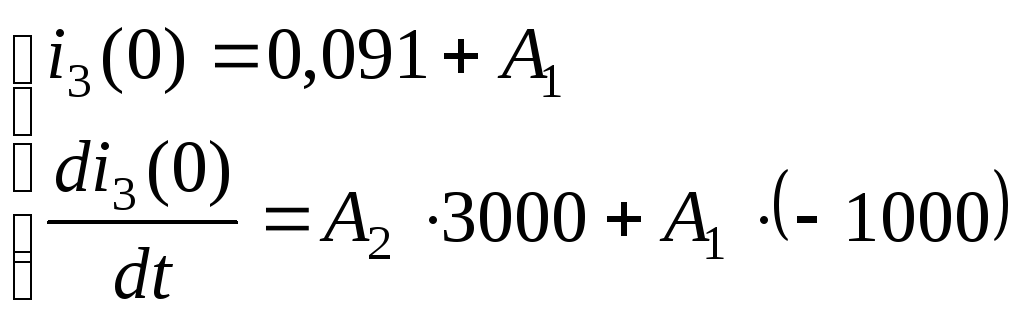
С учетом , получим:

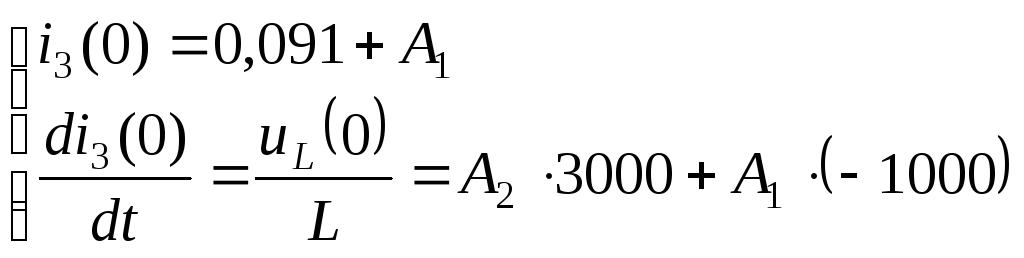
С учетом начальных условий получим:

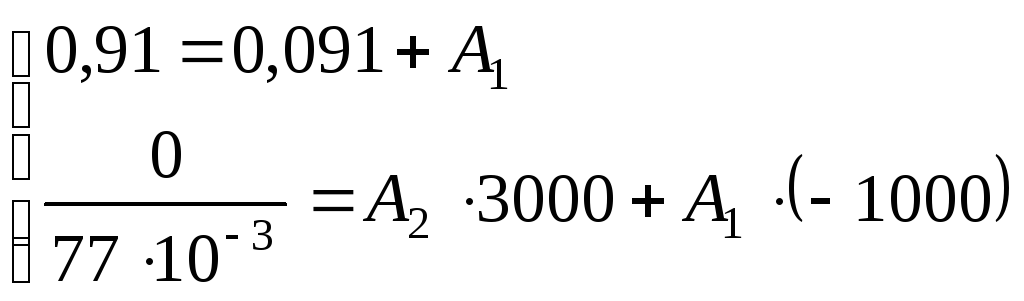
Отсюда: , .

Итак, получаем закон изменения тока индуктивности:

Определяем искомое напряжение индуктивности:

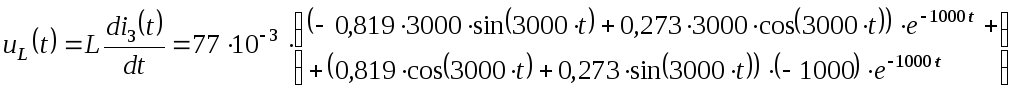
Пример 2

Операторный метод.

Определяем независимые начальные условия.

Выше уже были определены классическим методом ННУ:

.

.

Составим операторную схему замещения после коммутации.

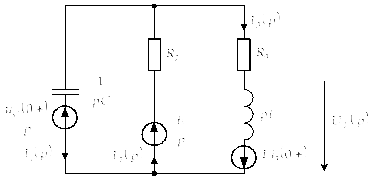
Система уравнений методом контурных токов:

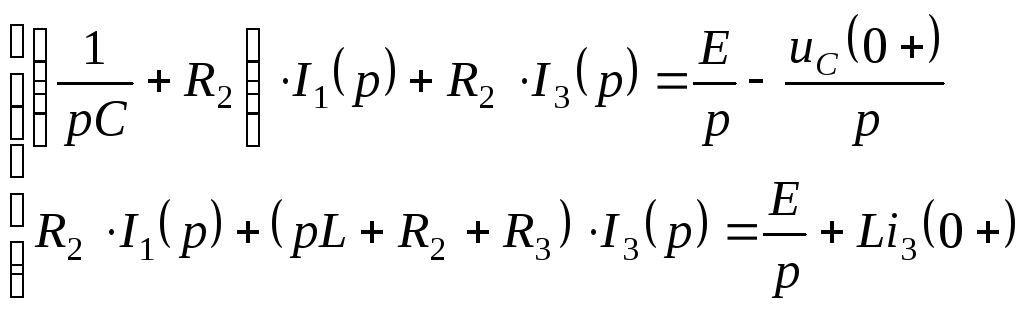
Подставляем числовые значения:

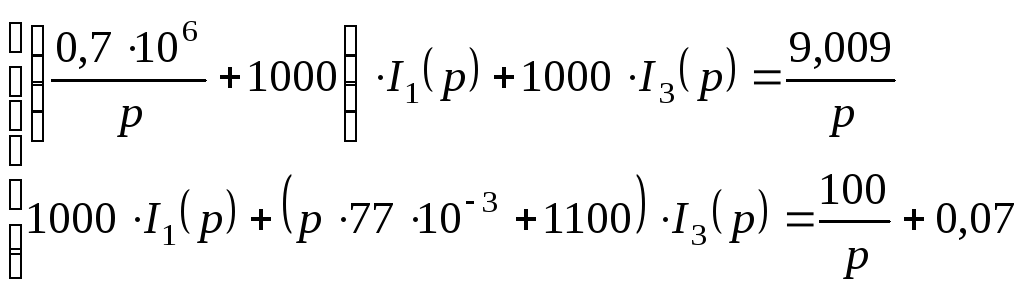
Из второго уравнения:

Подставляем в первое уравнение:

Определим изображение напряжения индуктивности:

.

Для нахождения оригиналов используем формулу разложения. Определим корни полинома знаменателя:

,

.

Т.к. корни комплексно сопряженные, то оригинал определим по следующей формуле разложения:

Коэффициенты при экспонентах в случае комплексно-сопряженных корней тоже будут комплексно-сопряженными, поэтому при суммировании мнимая часть будет равна нулю и ток можно определить, как удвоенное значение вещественной части первого или второго слагаемых:

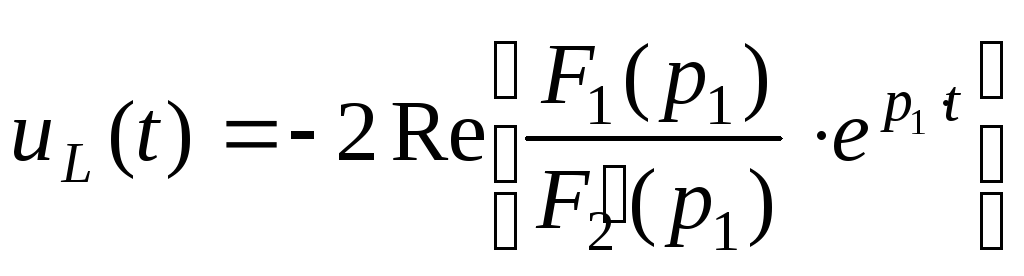
Здесь:

;

.

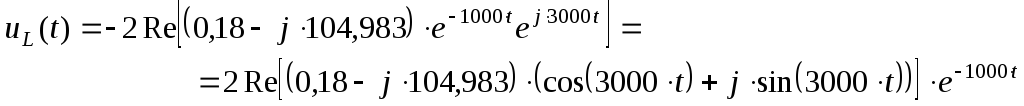
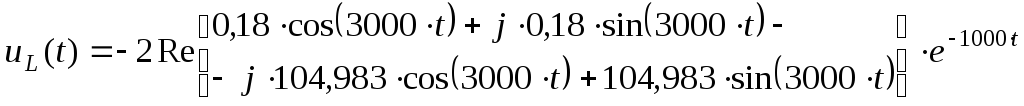
Как видно из полученных результатов, напряжение, рассчитанное операторным методом, совпадает с выражением, полученным классическим методом.

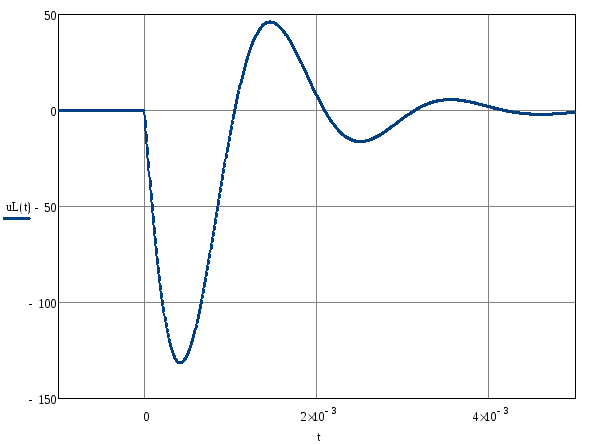
2. Построение графиков:

Построим график, учитывая, что переходной процесс в цепи практически заканчивается за время после коммутации.

Здесь постоянная цепи, равная:

.