
МАТЕМАТИКА ZIP File / Лек бак 2 семестр / Задачи
.docx
Задачи на составление дифференциальных уравнений
Задача 1. Поглощение света при прохождении через воду
Поглощение
светового потока тонким слоем воды
пропорционально толщине слоя и потоку,
падающему на его поверхность. Зная, что
при прохождении через слой толщиной 2м
поглощается
 первоначального светового потока,
определить, какой процент его дойдет
до глубины 12м ?
первоначального светового потока,
определить, какой процент его дойдет
до глубины 12м ?
Решение:
Составим
дифференциальное уравнение. Обозначим
через
 световой поток, падающий на поверхность
на глубине
световой поток, падающий на поверхность
на глубине
 .
При прохождении через слой воды толщиной
.
При прохождении через слой воды толщиной
 поглощенный световой поток
поглощенный световой поток
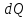 равен дифференциалу
равен дифференциалу
 ,
где
,
где
 – коэффициент пропорциональности (
– коэффициент пропорциональности ( ).
).
Общее
решение дифференциального уравнения
получаем путем разделения переменных
 .
В результате общее решение имеет вид:
.
В результате общее решение имеет вид:
 .
.
По
условию задачи при
 имеем
имеем
 поэтому
поэтому
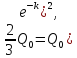 откуда
откуда
 и
и
 ,
,
До
глубины
 м
дойдет
световой поток
м
дойдет
световой поток
 что
составляет 8,78
что
составляет 8,78 первоначального светового потока.
первоначального светового потока.
Задача 2.
Найти
кривую, проходящую через точку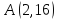 ,
зная,
что угловой коэффициент касательной в
любой точке кривой в три раза больше
углового коэффициента прямой, соединяющей
эту же точку с началом координат.
,
зная,
что угловой коэффициент касательной в
любой точке кривой в три раза больше
углового коэффициента прямой, соединяющей
эту же точку с началом координат.
Решение:
Пусть
 -
искомое
уравнение кривой. Проведем касательную
в произвольной точке
-
искомое
уравнение кривой. Проведем касательную
в произвольной точке
 .
Её
угловой коэффициент
.
Её
угловой коэффициент
 .
Согласно
условию он в три раза больше углового
коэффициента
прямой
.
Согласно
условию он в три раза больше углового
коэффициента
прямой
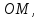 уравнение
которой
уравнение
которой
 Таким образом
Таким образом
 . Получили
уравнение с разделяющимися переменными.
Разделяя переменные
. Получили
уравнение с разделяющимися переменными.
Разделяя переменные
 и интегрируя, получим общее решение
и интегрируя, получим общее решение
 .
Так как искомая кривая проходит через
точку
.
Так как искомая кривая проходит через
точку
 ,
найдем
,
найдем
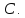
 тогда
искомое уравнение примет вид
тогда
искомое уравнение примет вид
 .
.
Задача 3.
Подкасательной
кривой
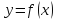 в точке
в точке
 называется проекция
называется проекция
 на
ось
на
ось
 отрезка
отрезка
 касательной
к этой кривой, где
касательной
к этой кривой, где
 точка
пересечения касательной с осью
точка
пересечения касательной с осью
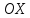 (рис.
1)
Найти семейство кривых, у которых
подкасательная имеет длину, равную 2.
(рис.
1)
Найти семейство кривых, у которых
подкасательная имеет длину, равную 2.
Решение:









Пусть
 -
искомое уравнение кривой. Проведем
касательную в произвольной точке
-
искомое уравнение кривой. Проведем
касательную в произвольной точке
 кривой
кривой
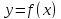 . Рассмотрим прямоугольный треугольник
. Рассмотрим прямоугольный треугольник
 .
.
 Согласно
условию
задачи
Согласно
условию
задачи
 .
Учитывая,
что
.
Учитывая,
что
 а
а
 получим дифференциальное уравнение
получим дифференциальное уравнение
 общее
решение которого имеет вид
общее
решение которого имеет вид

Задача 4.
Найти кривую, у которой сумма длин касательной (точнее длины её отрезка от точки касания до точки пересечения с осью абсцисс) и подкасательной в любой её точке равна произведению координат точки касания.
Решение:











Пусть
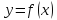 -
искомая функция. Проведем касательную
в произвольной точке
-
искомая функция. Проведем касательную
в произвольной точке
 кривой
кривой
 Согласно
условию задачи
Согласно
условию задачи
 .
.
Из
прямоугольного треугольника


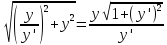
Тогда
дифференциальное уравнение примет вид

 ,
,
Умножая
обе части полученного уравнения на
дробь
 получим
получим
 .
.
Преобразуем
его.

Возводим
обе части в квадрат.

Разделим
обе части на
 (при условим, что
(при условим, что
 ).
).
 откуда
откуда
Разделяя переменные и интегрируя, получим общее решение

Задача 5.
Найти
уравнение кривой, проходящей через
точку
 у
которой подкасательная равна сумме
координат точки касания.
у
которой подкасательная равна сумме
координат точки касания.
Решение:




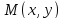

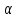




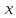
Пусть
 -
искомое уравнение кривой. Проведем
касательную в произвольной точке
-
искомое уравнение кривой. Проведем
касательную в произвольной точке
 По условию задачи длина подкасательной
По условию задачи длина подкасательной
 .
.
Из
прямоугольного треугольника
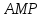 находим
находим
 т.е.
т.е.
 Решаем
полученное однородное уравнение с
помощью подстановки
Решаем
полученное однородное уравнение с
помощью подстановки
 откуда
откуда

Имеем
 т.е.
т.е.

Откуда
 , или
, или

Интегрируя полученное уравнение, имеем

 или
или

Так
как искомая кривая проходит через точку
 имеем
имеем
 или
или
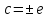
Таким
образом, искомой кривой является линия,
определяемая уравнением

 Задача
5.
Задача
5.
Сила
тока
 в
электрической цепи с сопротивлением
в
электрической цепи с сопротивлением
 коэффициентом
индуктивности
коэффициентом
индуктивности
 и
электродвижущей силой
и
электродвижущей силой
 удовлетворяет
дифференциальному уравнению
удовлетворяет
дифференциальному уравнению

Найти
зависимость силы тока
 от
времени, если
от
времени, если
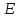 изменяется
по закону
изменяется
по закону
 и
и
 (
( ),
),

Решение:
Уравнение
 является линейным дифференциальным
уравнением первого порядка. Решим его
методом Бернулли, представляя искомую
функцию как
является линейным дифференциальным
уравнением первого порядка. Решим его
методом Бернулли, представляя искомую
функцию как
 .
Тогда производная равна
.
Тогда производная равна
 а уравнение преобразуется к виду
а уравнение преобразуется к виду
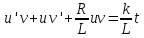 или
или
 (1)
(1)
Подберем
 так, чтобы выражение в скобках было
равно нулю, т.е. решаем дифференциальное
уравнение с разделяющимися переменными
так, чтобы выражение в скобках было
равно нулю, т.е. решаем дифференциальное
уравнение с разделяющимися переменными


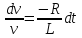 . После интегрирования получаем
. После интегрирования получаем
 .
.
Подставляя
найденное функции
 в уравнение (1), получим второе
дифференциальное уравнение с разделяющимися
переменными, из которого найдем функцию
в уравнение (1), получим второе
дифференциальное уравнение с разделяющимися
переменными, из которого найдем функцию



 =>
=>

Следовательно,
 К последнему интегралу применяем метод
интегрирования по частям и находим
К последнему интегралу применяем метод
интегрирования по частям и находим
 .
.
Окончательно
получаем общее решение:
 .
.
Принимая
во внимание, что
 находим
значение произвольной постоянной
находим
значение произвольной постоянной

 и
частное решение
и
частное решение
 .
.
Задача 6. Вентиляция цеха.
В
помещении цеха вместимости 10800 воздух содержит 0,12% углекислого газа.
Вентиляторы доставляют свежий воздух,
содержащий 0,04% углекислоты, в количестве
воздух содержит 0,12% углекислого газа.
Вентиляторы доставляют свежий воздух,
содержащий 0,04% углекислоты, в количестве

 мин.
Предполагая, что концентрация углекислоты
во всех частях помещения в каждый момент
времени одна и тоже, рассчитать какова
должна быть мощность вентиляторов,
чтобы по истечении 10мин содержание
углекислоты не превышало 0,06%.
мин.
Предполагая, что концентрация углекислоты
во всех частях помещения в каждый момент
времени одна и тоже, рассчитать какова
должна быть мощность вентиляторов,
чтобы по истечении 10мин содержание
углекислоты не превышало 0,06%.
Решение:
Обозначим
содержание углекислоты в воздухе в
момент времени
 через
через
 (%).
Составим за промежуток времени
(%).
Составим за промежуток времени
 мин,
протекший от момента
мин,
протекший от момента
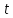 ,
баланс углекислоты, находящейся в
помещении. За это время вентиляторы
доставили 0,0004
,
баланс углекислоты, находящейся в
помещении. За это время вентиляторы
доставили 0,0004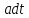
 углекислоты,
а ушло из помещения 0,01
углекислоты,
а ушло из помещения 0,01 Значит всего за
Значит всего за
 мин,
количество углекислоты в воздухе
уменьшилось на
мин,
количество углекислоты в воздухе
уменьшилось на

Обозначив
через
 процентное
уменьшение содержания углекислоты в
воздухе, можно подсчитать это же
количество углекислоты другим путем,
по формуле
процентное
уменьшение содержания углекислоты в
воздухе, можно подсчитать это же
количество углекислоты другим путем,
по формуле
 (знак минус берется потому, что
(знак минус берется потому, что
 ).
).
Приравнивая
друг другу оба выражения для
 ,
составим
дифференциальное уравнение
(
,
составим
дифференциальное уравнение
(
Разделяя
переменные, найдем
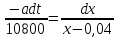 . Общий интеграл имеет вид
. Общий интеграл имеет вид
 или
или
 .
Поскольку.
.
Поскольку.
 при
при
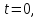 то
то
 и
частное решение имеет вид
и
частное решение имеет вид

Для
определения мощности
 вентиляторов
положим
вентиляторов
положим
 и
и
 получаем
получаем
 откуда
откуда
 и
и

